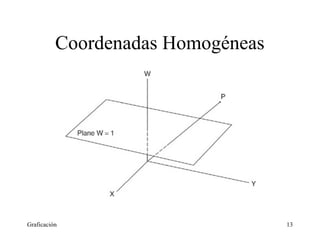
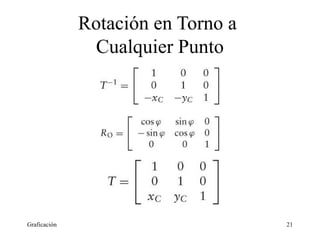
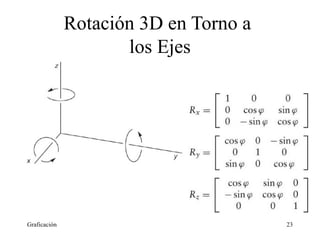
Este documento describe diferentes tipos de transformaciones geométricas, incluyendo rotaciones, escalamiento, acizallamiento, translaciones y rotaciones en 3D. Explica cómo estas transformaciones pueden representarse mediante productos de matrices y coordenadas homogéneas. También cubre conceptos como transformaciones inversas y rotaciones en torno a puntos arbitrarios.

1. Graficación
IA7200-T
Transformaciones Geométricas

2. Transformaciones Geométricas
• Producto Matricial
• Transformaciones
Lineales
• Rotaciones
• Escalamiento
• Acizallamiento
• Translaciones
• Coordenadas Homogéneas
• Transformaciones Inversas
• Rotaciones Arbitrarias
• Cambio de Coordenadas
• Rotaciones 3D
Graficación 2

3. Producto Matricial
Graficación 3

4. Transformaciones Lineales
Una transformación T es un mapeo
Una transformación es lineal si para todos v y
w (vectores) y λ (real)
Si T es lineal:
Graficación 4

5. Transformaciones Lineales
En el espacio x-y, asociemos un punto P al
vector V, tal que:
T es un mapeo de puntos a puntos:
Para todo punto P en x-y, donde:
Graficación 5
v ¢ = OP ′

6. Transformaciones Lineales
Las TLs pueden ser escritas como un producto
de matrices. Por ejemplo
Se puede escribir como el producto
Graficación 6

7. Transformaciones Lineales
Ejemplo:
Los renglones de T
son las imágenes de
(1,0) y (0,1)
Graficación 7

8. Rotación
Graficación 8

9. Escalamiento
Graficación 9

10. Acizallamiento
Graficación 10

11. Translaciones
¿Cuál es la matriz T para translaciones?
T no es lineal (i.e. T(0) = (a,b)≠0)
(a,b) se llama vector de desplazamiento
(shift vector)
Graficación 11

12. Coordenadas Homogéneas
Para combinar todas las transfomaciones vistas hasta aquí,
añadimos una dimensión mas, W.
La dimensión extra hace que P=(x,y) tenga toda una familia de
representaciones coordenadas (wx, wy, w) w≠0.
Por ejemplo, (3,6,1), (0.3,0.6,0.1), (6,12,2), (12,24,4), etc.
Cuando un punto se mapea al plano W=1, se dice que está
homogeneizado.
Conversión:
(x,y)  (x,y,1)
(wx,wy,w)  (wx/w, wy/w)
Graficación 12

13. Coordenadas Homogéneas
Graficación 13

14. Coordenadas Homogéneas
T en coordenadas homogéneas
Translación
Rotación
Graficación 14

15. Ejercicios
• Dibuje un rectángulo unitario en un espacio R2
• Genere una matriz T1 para una rotación de 15°
• Genere una matriz T2 para un escalamiento de 1.5 en
x y 2 en y
• Genere una matriz T3 para un acizallamiento de 0.5
en la horizontal
• Combínelas, para formar una sola matriz T de
transformación que además desplace el rectángulo
por (1, 0.5)
• Aplique la matriz resultante al rectángulo
Graficación 15

16. Ejercicios
Ver Programa de Mathematica
Graficación 16

17. Transformaciones Inversas
• Si R mapea de P a P’, la inversa mapea de P’ a P.
• Ej. Rotación Inversa
• Se debe cumplir que
Graficación 17

18. Transformaciones Inversas
• Sin embargo, no todas las transformaciones son
reversibles
• Ej. Una transformación que mapea de cualquier
punto al eje x no lo es.
• La matriz no tiene inversa
• Para que una matriz tenga inversa, su determinante
debe ser diferente de cero
Graficación 18

19. Transformaciones Inversas
• La matriz de transformación del mapeo
Graficación 19

20. Rotación en Torno a
Cualquier Punto
• No es lineal
• Puede ser descrita como un producto matricial
(coordenadas homogéneas)
• La rotación en el punto C(Xc, Yc) en un ángulo φ se
puede hacer en tres pasos:
• Translación al origen
• Rotación en el origen
• Translación de regreso
Graficación 20

21. Rotación en Torno a
Cualquier Punto
Graficación 21

22. Rotación en Torno a
Cualquier Punto
Graficación 22

23. Rotación 3D en Torno a
los Ejes
Graficación 23

24. Rotación 3D en Torno a
un Eje Arbitrario
1. Rotación en z -θ
2. Rotación en y -φ
3. Rotación en z α
4. Rotación en y φ
5. Rotación en z θ
Graficación 24

25. Rotación 3D en Torno a
un Eje Arbitrario
Graficación 25

26. Rotación 3D en Torno a
un Eje Arbitrario
Si el punto de inicio no es el origen, sino un punto
arbitrario A(a1,a2,a3)
a. Translación de A a O
b. La rotación R, descrita anteriormente
c. Translación inversa de O a A
Graficación 26

27. Rotación 3D en Torno a
un Eje Arbitrario
Graficación 27