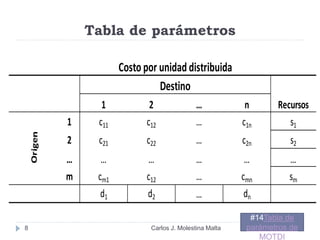
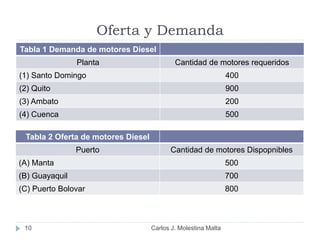
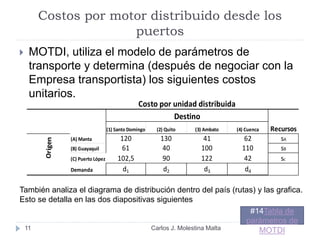
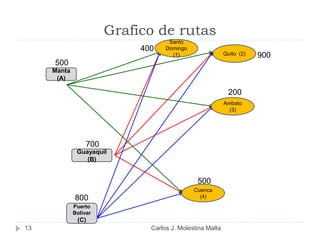
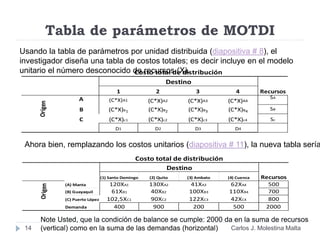
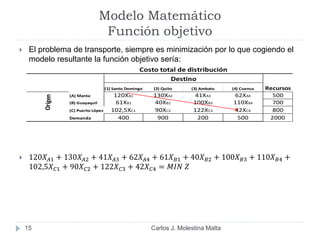
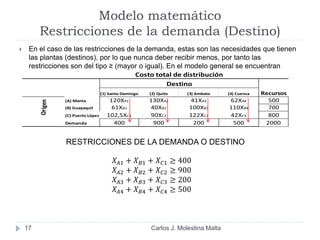
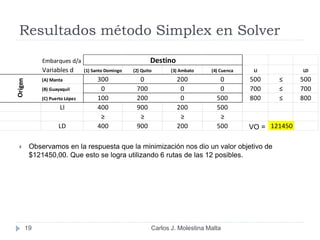
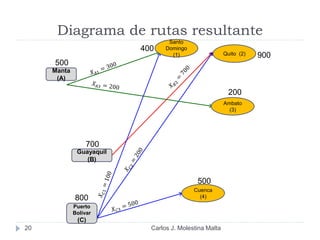
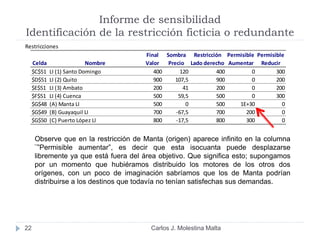
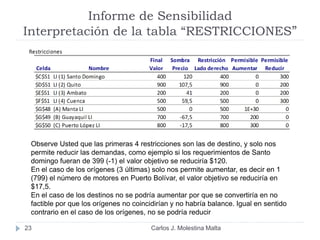
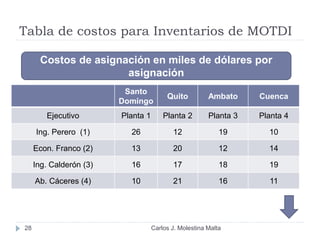
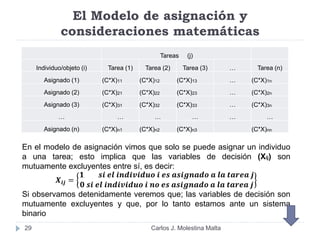
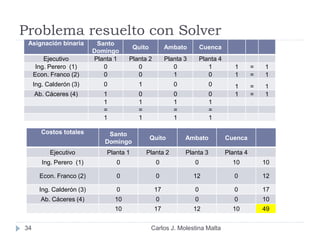
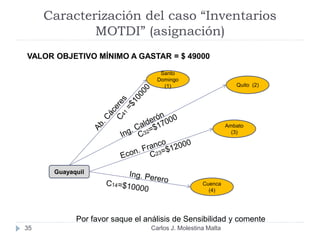
Este documento resume un modelo de programación lineal para la distribución de motores diésel desde puertos a plantas de ensamblaje en Ecuador. El objetivo es minimizar los costos totales de distribución utilizando la oferta disponible en los puertos y satisfaciendo la demanda de las plantas. El modelo contiene una función objetivo que suma los costos de cada ruta posible, y restricciones en la oferta de los puertos y la demanda de las plantas. La solución utiliza el método simplex en Solver para encontrar la distribución ópt