Descargar para leer sin conexión
Subido porJonathan Miguel Mendoza
Identidades demostraciones
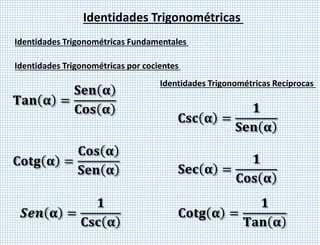
El documento aborda diversas identidades trigonométricas, incluyendo identidades fundamentales, recíprocas y pitagóricas, así como fórmulas de suma y diferencia de ángulos. También se detallan métodos para demostrar y simplificar expresiones trigonométricas mediante la manipulación algebraica y la reescritura en términos de senos y cosenos. Se incluyen ejemplos prácticos de simplificación y demostración de identidades trigonométricas, junto con fórmulas relevantes para distintos ángulos.
Más contenido relacionado
Similar a Identidades demostraciones
Identidades demostraciones
- 1. Identidades Trigonométricas Identidades TrigonométricasFundamentales Identidades Trigonométricas por cocientes 𝐓𝐚𝐧 𝛂 = 𝐒𝐞𝐧 𝛂 𝐂𝐨𝐬 𝛂 𝐂𝐨𝐭𝐠 𝛂 = 𝐂𝐨𝐬 𝛂 𝐒𝐞𝐧 𝛂 Identidades Trigonométricas Recíprocas 𝐂𝐬𝐜 𝛂 = 𝟏 𝐒𝐞𝐧 𝛂 𝐒𝐞𝐜 𝛂 = 𝟏 𝐂𝐨𝐬 𝛂 𝐂𝐨𝐭𝐠 𝛂 = 𝟏 𝐓𝐚𝐧 𝛂 𝑺𝒆𝒏 𝛂 = 𝟏 𝐂𝐬𝐜 𝛂
- 2. Identidades Trigonométricas Pitagóricaso Cuadráticas 𝐓𝐚𝐧 𝟐 𝛂 = 𝐒𝐞𝐧 𝟐 𝛂 𝐂𝐨𝐬 𝟐 𝛂 𝐂𝐨𝐭𝐠 𝟐 𝛂 = 𝐂𝐨𝐬 𝟐 𝛂 𝐒𝐞𝐧 𝟐 𝛂 𝐂𝐬𝐜 𝟐 𝛂 = 𝟏 𝐒𝐞𝐧 𝟐 𝛂 𝐒𝐞𝐜 𝟐 𝛂 = 𝟏 𝐂𝐨𝐬 𝟐 𝛂 𝐂𝐬𝐜 𝟐 𝛂 = 𝟏 𝐒𝐞𝐧 𝟐 𝛂 𝐂𝐨𝐭𝐠 𝟐 𝛂 = 𝟏 𝐓𝐚𝐧 𝟐 𝛂
- 3. Identidades Trigonométricas Pitagóricaso Cuadráticas 𝐒𝐞𝐧 𝟐 𝛂 + 𝐂𝐨𝐬 𝟐 𝛂 = 𝟏 𝐒𝐞𝐧 𝟐 𝛂 = 𝟏 − 𝐂𝐨𝐬 𝟐 𝛂 𝐂𝐨𝐬 𝟐 𝛂 = 𝟏 − 𝐒𝐞𝐧 𝟐 𝛂 𝐓𝐚𝐧 𝟐 𝛂 + 𝟏 = 𝐒𝐞𝐜 𝟐 𝛂 𝐂𝐨𝐭𝐠 𝟐 𝛂 + 𝟏 = 𝐂𝐬𝐜 𝟐 𝛂 𝐓𝐚𝐧 𝟐 𝛂 = 𝐒𝐞𝐜 𝟐 𝛂 − 𝟏 𝐂𝐨𝐭𝐠 𝟐 𝛂 = 𝐂𝐬𝐜 𝟐 𝛂 − 𝟏
- 4. DEMOSTRACIONES O SIMPLIFICACIÓNde Identidades Trigonométricas Reglas Generales para Simplificar una Expresión Trigonométrica O para demostrar una Identidad Trigonométrica Primero) Se identifica el lado más complejo de la identidad o igualdad. Segundo) Se expresan todos los términos de la igualdad en función de senos y cosenos. Tercero) Se efectúan las operaciones indicadas, y se simplifica lo más que se pueda. Cuarto) Encontrar un Mínimo Común Múltiplo (M.C.M.) si la identidad es expresada por medio de una fracción. Quinto) Factorizar las expresiones que son factorables, si el caso lo amerita. Nota: A medida que cada expresión o igualdad lo amerite se deben utilizar los artificios matemáticos de lugar. Recordar tener pendientes los postulados básicos del álgebra.
- 5. 𝒕𝒂𝒏𝝋 𝟏 + 𝑺𝒆𝒄𝝋 + 𝟏+ 𝑺𝒆𝒄𝝋 𝒕𝒂𝒏𝝋 Empecemos. ¡Advertencia! Este tema no es para personas dejadas Simplificar la expresión: Expresamos todo en función de Senos y Cosenos 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 1 + 1 𝑪𝒐𝒔𝝋 + 1 + 1 𝑪𝒐𝒔𝝋 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 = 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 𝑪𝒐𝒔𝝋 + 1 𝑪𝒐𝒔𝝋 + 𝑪𝒐𝒔𝝋 + 1 𝑪𝒐𝒔𝝋 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 Ahora simplificamos: = 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 + 1 + 𝑪𝒐𝒔𝝋 + 1 𝑺𝒆𝒏𝝋
- 6. Sumamos las fraccionespor la propiedad fundamental: 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 + 1 + 𝑪𝒐𝒔𝝋 + 1 𝑺𝒆𝒏𝝋 = 𝑺𝒆𝒏2 𝝋 + 𝑪𝒐𝒔𝝋 + 1 2 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 + 1 Desarrollamos y tenemos que: 𝑺𝒆𝒏2 𝝋 + 𝑪𝒐𝒔𝝋 + 1 2 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 + 1 = 𝑺𝒆𝒏2 𝝋 + 𝑪𝒐𝒔2 𝝋 + 2𝑪𝒐𝒔𝝋 + 1 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 + 1 𝑺𝒆𝒏2 𝝋 + 𝑪𝒐𝒔2 𝝋 + 2𝑪𝒐𝒔𝝋 + 1 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 + 1 = 𝟏 + 2𝑪𝒐𝒔𝝋 + 1 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 + 1 2𝑪𝒐𝒔𝝋 + 2 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 + 1 = 2 𝑪𝒐𝒔𝝋 + 1 𝑺𝒆𝒏𝝋 𝑪𝒐𝒔𝝋 + 1 = 𝟐 𝐒𝐞𝐧𝛗 = 𝟐𝑪𝒔𝒄𝝋
- 7. Simplificar la expresión:𝐂𝐨𝐬 90° − 𝛟 𝐒𝐞𝐧 𝛟 − 180° 𝐂𝐨𝐬 90° − 𝛟 𝐒𝐞𝐧 𝛟 − 180° = 𝑪𝒐𝒔𝟗𝟎°𝑪𝒐𝒔𝛟 + 𝐒𝐞𝐧𝟗𝟎°𝐒𝐞𝐧𝛟 𝐒𝐞𝐧𝛟𝐂𝐨𝐬𝟏𝟖𝟎° − 𝐂𝐨𝐬𝛟𝐒𝐞𝐧𝟏𝟖𝟎° 𝑪𝒐𝒔𝟗𝟎°𝑪𝒐𝒔𝛟 + 𝐒𝐞𝐧𝟗𝟎°𝐒𝐞𝐧𝛟 𝐒𝐞𝐧𝛟𝐂𝐨𝐬𝟏𝟖𝟎° − 𝐂𝐨𝐬𝛟𝐒𝐞𝐧𝟏𝟖𝟎° = 𝟎 𝑪𝒐𝒔𝛟 + 𝟏 𝐒𝐞𝐧𝛟 𝐒𝐞𝐧𝛟 −𝟏 − 𝐂𝐨𝐬𝛟(𝟎) = 𝟎 𝑪𝒐𝒔𝛟 + 𝟏 𝐒𝐞𝐧𝛟 𝐒𝐞𝐧𝛟 −𝟏 − 𝐂𝐨𝐬𝛟(𝟎) = 𝐒𝐞𝐧𝛟 −𝐒𝐞𝐧𝛟 = −𝟏 𝐂𝐨𝐬 90° − 𝛟 𝐒𝐞𝐧 𝛟 − 180° ≡ 𝟏
- 8. Simplificar la expresión: 𝐓𝐚𝐧𝛃𝐂𝐬𝐜𝛃+ 𝟓𝐂𝐬𝐜𝛃𝐒𝐞𝐧𝛃 = 𝐒𝐞𝐧𝛃 𝐂𝐨𝐬𝛃 𝟏 𝐒𝐞𝐧𝛃 + 𝟓 𝟏 𝐒𝐞𝐧𝛃 𝐒𝐞𝐧𝛃 = 𝐒𝐞𝐧𝛃 𝐂𝐨𝐬𝛃 𝟏 𝐒𝐞𝐧𝛃 + 𝟓 𝟏 𝐒𝐞𝐧𝛃 𝐒𝐞𝐧𝛃 = 𝟏 𝐂𝐨𝐬𝛃 + 𝟓(𝟏) = 𝑺𝒆𝒄𝜷 + 𝟓 P𝐞𝐫𝐨; 𝐒𝐞𝐜𝛃 = 𝟏 𝐂𝐨𝐬𝛃 𝐓𝐚𝐧𝛃𝐂𝐬𝐜𝛃 + 𝟓𝐂𝐬𝐜𝛃𝐒𝐞𝐧𝛃 ≡ 𝑺𝒆𝒄𝜷 + 𝟓
- 9. Simplificar la expresión:𝐓𝐚𝐧𝛃 + 𝐒𝐞𝐧𝛃 𝟏 + 𝐂𝐨𝐬𝛃 1°) Expresamos la Tanβ como Senβ/Cosβ: 𝐓𝐚𝐧𝛃 + 𝐒𝐞𝐧𝛃 𝟏 + 𝐂𝐨𝐬𝛃 = 𝐒𝐞𝐧β 𝑪𝒐𝒔𝜷 + 𝑺𝒆𝒏𝜷 𝟏 + 𝑪𝒐𝒔𝜷 𝐒𝐞𝐧β 𝑪𝒐𝒔𝜷 + 𝑺𝒆𝒏𝜷 𝟏 + 𝑪𝒐𝒔𝜷 = 𝑺𝒆𝒏𝜷 + 𝑺𝒆𝒏𝜷𝑪𝒐𝒔𝜷 𝑪𝒐𝒔𝜷 𝟏 + 𝑪𝒐𝒔𝜷 𝐒𝐞𝐧𝛃 + 𝐒𝐞𝐧𝛃𝐂𝐨𝐬𝛃 𝐂𝐨𝐬𝛃 × 𝟏 𝟏 + 𝐂𝐨𝐬𝛃 2°) Reescribimos la expresión:
- 10. 𝐒𝐞𝐧𝛃 + 𝐒𝐞𝐧𝛃𝐂𝐨𝐬𝛃 𝐂𝐨𝐬𝛃 × 𝟏 𝟏+ 𝐂𝐨𝐬𝛃 3°) Extraemos el factor común del primer Factor: 𝐒𝐞𝐧𝛃 𝐒𝐞𝐧𝛃(𝟏 + 𝐂𝐨𝐬𝛃) 𝐂𝐨𝐬𝛃 × 𝟏 𝟏 + 𝐂𝐨𝐬𝛃 4°) Eliminamos el factor común del primer Factor y el segundo: 𝟏 + 𝐂𝐨𝐬𝛃 𝐒𝐞𝐧𝛃 𝐂𝐨𝐬𝛃 × 𝟏 = 𝐒𝐞𝐧𝛃 𝐂𝐨𝐬𝛃 → 𝐒𝐞𝐧𝛃 𝐂𝐨𝐬𝛃 = 𝑻𝒂𝒏𝜷 𝐓𝐚𝐧𝛃 + 𝐒𝐞𝐧𝛃 𝟏 + 𝐂𝐨𝐬𝛃 ≡ 𝑻𝒂𝒏𝜷
- 11. Demostrar que: 𝐂𝐬𝐜𝛃 𝐓𝐚𝐧𝛃+ 𝐂𝐨𝐭𝒈𝛃 = 𝐂𝐨𝐬𝛃 1°) Expresamos todas las funciones en términos de Senβ y Cosβ: 𝐂𝐬𝐜𝛃 𝐓𝐚𝐧𝛃 + 𝐂𝐨𝐭𝒈𝛃 = 𝟏 𝐒𝐞𝐧𝛃 𝐒𝐞𝐧𝛃 𝑪𝒐𝒔𝜷 + 𝑪𝒐𝒔𝜷 𝑺𝒆𝒏𝜷 𝟏 𝐒𝐞𝐧𝛃 𝐒𝐞𝐧𝛃 𝑪𝒐𝒔𝜷 + 𝑪𝒐𝒔𝜷 𝑺𝒆𝒏𝜷 = 𝟏 𝑺𝒆𝒏𝜷 ÷ 𝑺𝒆𝒏 𝟐 𝜷 + 𝑪𝒐𝒔 𝟐 𝜷 𝑺𝒆𝒏𝜷𝑪𝒐𝒔𝜷 2°) Reescribimos toda la expresión:
- 12. 𝟏 𝐒𝐞𝐧𝛃 ÷ 𝐒𝐞𝐧 𝟐 𝛃+𝐂𝐨𝐬𝟐 𝛃 𝐒𝐞𝐧𝛃𝐂𝐨𝐬𝛃 = 𝟏 𝐒𝐞𝐧𝛃 × 𝐒𝐞𝐧𝛃𝐂𝐨𝐬𝛃 𝐒𝐞𝐧 𝟐 𝛃+𝐂𝐨𝐬 𝟐 𝛃 3°) Volvemos a Reescribir toda la expresión: 𝟏 𝑺𝒆𝒏𝜷 × 𝑺𝒆𝒏𝜷𝑪𝒐𝒔𝜷 𝑺𝒆𝒏 𝟐 𝜷+𝑪𝒐𝒔 𝟐 𝜷 = 𝟏 × 𝑪𝒐𝒔𝜷 𝟏 4°) Simplificamos los factores comunes: 𝟏 × 𝐂𝐨𝐬𝛃 𝟏 = 𝐂𝐨𝐬𝛃 Por lo tanto: 𝐂𝐬𝐜𝛃 𝐓𝐚𝐧𝛃 + 𝐂𝐨𝐭𝒈𝛃 ≡ 𝐂𝐨𝐬𝛃 1
- 13. Para demostrar algunasidentidades trigonométricas, en ocasiones también debemos manipular algebraicamente ambos lados de la igualdad. También, debemos tener en cuenta las siguientes fórmulas: I) Fórmulas de la suma y diferencia de dos ángulos. 𝑺𝐞𝐧 𝛂 + 𝛃 = 𝐒𝐞𝐧𝛂 • 𝐂𝐨𝐬𝛃 + 𝐂𝐨𝐬𝛂 • 𝐒𝐞𝐧𝛃 𝑺𝐞𝐧 𝛂 − 𝛃 = 𝐒𝐞𝐧𝛂 • 𝐂𝐨𝐬𝛃 − 𝐂𝐨𝐬𝛂 • 𝐒𝐞𝐧𝛃
- 14. 𝐂𝐨𝐬 𝛂 +𝛃 = 𝐂𝐨𝐬𝛂 • 𝐂𝐨𝐬𝛃 − 𝐒𝐞𝐧𝛂 • 𝐒𝐞𝐧𝛃 𝐂𝐨𝐬 𝛂 − 𝛃 = 𝑪𝒐𝒔𝛂 • 𝐂𝐨𝐬𝛃 + 𝐒𝐞𝐧𝛂 • 𝐒𝐞𝐧𝛃 𝐓𝐚𝐧 𝛂 + 𝛃 = 𝐓𝐚𝐧𝛂 + 𝐓𝐚𝐧𝛃 1 − 𝐓𝐚𝐧𝛂 • 𝐓𝐚𝐧𝛃 𝐓𝐚𝐧 𝛂 − 𝛃 = 𝐓𝐚𝐧𝛂 − 𝐓𝐚𝐧𝛃 1 + 𝐓𝐚𝐧𝛂 • 𝐓𝐚𝐧𝛃 𝐂𝐨𝐭𝐠 𝛂 + 𝛃 = 𝐂𝐨𝐭𝐠𝛂 • 𝐂𝐨𝐭𝐠𝛃 − 1 𝐂𝐨𝐭𝐠𝛂 + 𝐂𝐨𝐭𝐠𝛃
- 15. 𝐂𝐨𝐭𝐠 𝛂 −𝛃 = 𝐂𝐨𝐭𝐠𝛂 • 𝐂𝐨𝐭𝐠𝛃 + 1 𝐂𝐨𝐭𝐠𝛃 − 𝐂𝐨𝐭𝐠𝛂 II) Fórmulas de los ángulos doble y triple. 𝐒𝐞𝐧 2𝛂 = 2𝐒𝐞𝐧𝛂 • 𝐂𝐨𝐬𝛂 𝐂𝐨𝐬 2𝛂 = 𝐂𝐨𝐬2 𝛂 − 𝐒𝐞𝐧2 𝜶 𝐓𝐚𝐧 2𝛂 = 2𝑻𝒂𝒏𝛂 1 − 𝐓𝐚𝐧2 𝜶 𝐒𝐞𝐧 3𝛃 = 3𝐒𝐞𝐧𝛃 − 4𝐒𝐞𝐧3 𝜷 𝐂𝐨𝐬 3𝛃 = 4𝐂𝐨𝐬3 𝛃 − 3𝐂𝐨𝐬𝛃
- 16. 𝐓𝐚𝐧 3𝛃 = 3𝑻𝒂𝒏𝛃− 𝐓𝐚𝐧3 𝛃 1 − 3𝐓𝐚𝐧2 𝛃 III) Fórmulas de los ángulos mitad. 𝐒𝐞𝐧 1 2 𝛂 = 1 2 1 − 𝐂𝐨𝐬𝜶 𝑪𝐨𝐬 𝟏 𝟐 𝛂 = 𝟏 𝟐 𝟏 + 𝐂𝐨𝐬𝜶
- 17. 𝑻𝐚𝐧 𝟏 𝟐 𝛂 = 𝟏 −𝐂𝐨𝐬𝜶 𝟏 + 𝐂𝐨𝐬𝜶 Otras formas de la tangente son: 𝐓𝐚𝐧 1 2 𝛂 = 1 − 𝐂𝐨𝐬𝛂 𝐒𝐞𝐧𝛂 𝐓𝐚𝐧 1 2 𝛂 = 𝐒𝐞𝐧𝛂 1 + 𝐂𝐨𝐬𝛂
- 18. IV) Fórmulas deTransformación de Suma y Resta de dos ángulos a Producto. 𝐒𝐞𝐧𝛂 + 𝐒𝐞𝐧𝛃 = 2𝐒𝐞𝐧 1 2 𝛂 + 𝛃 𝐂𝐨𝐬 1 2 𝛂 − 𝛃 𝐒𝐞𝐧𝛂 − 𝐒𝐞𝐧𝛃 = 2𝐒𝐞𝐧 1 2 𝛂 − 𝛃 𝐂𝐨𝐬 1 2 𝛂 + 𝛃 𝐂𝐨𝐬𝛂 + 𝐂𝐨𝐬𝛃 = 2𝐂𝐨𝐬 1 2 𝛂 + 𝛃 𝐂𝐨𝐬 1 2 𝛂 − 𝛃 𝐂𝐨𝐬𝛂 − 𝐂𝐨𝐬𝛃 = −2𝐒𝐞𝐧 1 2 𝛂 + 𝛃 𝐒𝐞𝐧 1 2 𝛂 − 𝛃
- 19. 𝐓𝐚𝐧𝛂 + 𝐓𝐚𝐧𝛃= 𝐒𝐞𝐧 𝛂 + 𝛃 𝐂𝐨𝐬𝛂𝐂𝐨𝐬𝛃 𝐓𝐚𝐧𝛂 − 𝐓𝐚𝐧𝛃 = 𝐒𝐞𝐧 𝛂 − 𝛃 𝐂𝐨𝐬𝛂𝐂𝐨𝐬𝛃 V) Fórmulas de Transformación de Producto de dos ángulos a Suma y Resta. 𝐒𝐞𝐧𝛂 • 𝐒𝐞𝐧𝛃 = 1 2 𝐂𝐨𝐬 𝛂 − 𝛃 − 𝐂𝐨𝐬 𝛂 + 𝛃 𝐂𝐨𝐬𝛂 • 𝐂𝐨𝐬𝛃 = 1 2 𝐂𝐨𝐬 𝛂 − 𝛃 + 𝐂𝐨𝐬 𝛂 + 𝛃
- 20. 𝐒𝐞𝐧𝛂 • 𝐂𝐨𝐬𝛃= 1 2 𝐒𝐞𝐧 𝛂 + 𝛃 + 𝐒𝐞𝐧 𝛂 − 𝛃 𝐒𝐞𝐧𝛃 • 𝐂𝐨𝐬𝛂 = 1 2 𝐒𝐞𝐧 𝛂 + 𝛃 − 𝐒𝐞𝐧 𝛂 − 𝛃 VI) Fórmulas de Transformación de Potencias Razones Trigonométricas. 𝐒𝐞𝐧2 𝛃 = 1 2 1 − 𝐂𝐨𝐬2𝛃 𝐒𝐞𝐧3 𝛃 = 1 4 3𝐒𝐞𝐧𝛃 − 𝐒𝐞𝐧 3𝛃
- 21. 𝐂𝐨𝐬2 𝛃 = 1 2 1 +𝐂𝐨𝐬2𝛃 𝐂𝐨𝐬3 𝛃 = 1 4 3𝐂𝐨𝐬𝛃 + 𝐂𝐨𝐬 3𝛃 𝐓𝐚𝐧2 𝛃 = 1 − 𝐂𝐨𝐬2𝛃 1 + 𝐂𝐨𝐬2𝛃 𝐓𝐚𝐧3 𝛃 = 3𝐒𝐞𝐧𝛃 − 𝐒𝐞𝐧 3𝛃 3𝐂𝐨𝐬𝛃 + 𝐂𝐨𝐬 3𝛃
- 22. VII) Fórmulas deFunciones (Razones) Trigonométricas. Del Primer Cuadrante: 𝐒𝐞𝐧𝛂 = 𝐲 𝐑 𝐂𝐬𝐜𝛂 = 𝐑 𝐲 𝐂𝐨𝐬𝛂 = 𝐱 𝐑 𝐒𝐞𝐜𝛂 = 𝐑 𝐱 𝐓𝐚𝐧𝛂 = 𝐲 𝐱 𝐂𝐨𝐭𝐠𝛂 = 𝐱 𝐲
- 23. Del Segundo Cuadrante: 𝐒𝐞𝐧(𝟏𝟖𝟎°− 𝛂) = 𝐒𝐞𝐧𝛂 𝐂𝐬𝐜(𝟏𝟖𝟎° − 𝛂) = 𝐂𝐬𝐜𝛂 𝐂𝐨𝐬 𝟏𝟖𝟎° − 𝛂 = −𝐂𝐨𝐬𝛂 𝐒𝐞𝐜 𝟏𝟖𝟎° − 𝛂 = −𝐒𝐞𝐜𝛂 𝐓𝐚𝐧 𝟏𝟖𝟎° − 𝛂 = −𝐓𝐚𝐧𝛂 𝐂𝐨𝐭𝐠 𝟏𝟖𝟎° − 𝛂 = −𝐂𝐨𝐭𝐠𝛂
- 24. Del Tercer Cuadrante: 𝐒𝐞𝐧𝟏𝟖𝟎° + 𝛂 = −𝐒𝐞𝐧𝛂 𝐂𝐬𝐜 𝟏𝟖𝟎° + 𝛂 = −𝐂𝐬𝐜𝛂 𝐂𝐨𝐬 𝟏𝟖𝟎° + 𝛂 = −𝐂𝐨𝐬𝛂 𝐒𝐞𝐜 𝟏𝟖𝟎° + 𝛂 = −𝐒𝐞𝐜𝛂 𝐓𝐚𝐧 𝟏𝟖𝟎° + 𝛂 = 𝐓𝐚𝐧𝛂 𝐂𝐨𝐭𝐠 𝟏𝟖𝟎° + 𝛂 = 𝐂𝐨𝐭𝐠𝛂
- 25. Del Cuarto Cuadrante: 𝐒𝐞𝐧𝟑𝟔𝟎° − 𝛂 = −𝐒𝐞𝐧𝛂 𝐂𝐬𝐜 𝟑𝟔𝟎° − 𝛂 = −𝐂𝐬𝐜𝛂 𝐂𝐨𝐬 𝟑𝟔𝟎° − 𝛂 = 𝐂𝐨𝐬𝛂 𝐒𝐞𝐜 𝟑𝟔𝟎° − 𝛂 = 𝐒𝐞𝐜𝛂 𝐓𝐚𝐧 𝟑𝟔𝟎° − 𝛂 = −𝐓𝐚𝐧𝛂 𝐂𝐨𝐭𝐠 𝟑𝟔𝟎° − 𝛂 = −𝐂𝐨𝐭𝐠𝛂
- 26. Demostrar que: 𝐒𝐞𝐜 𝟐 𝐱𝐂𝐨𝐬𝐱+ 𝐓𝐚𝐧𝐱𝐂𝐬𝐜𝐱 = 𝟐𝐒𝐞𝐜𝐱 𝟏 𝐂𝐨𝐬 𝟐 𝐱 𝐂𝐨𝐬𝐱 + 𝐒𝐞𝐧𝐱 𝐂𝐨𝐬𝐱 𝟏 𝐒𝐞𝐧𝐱 = 𝟐𝐒𝐞𝐜𝐱 Expresamos en términos de Seno y Cosenos. 𝟏 𝐂𝐨𝐬 𝟐 𝐱 𝐂𝐨𝐬𝐱 + 𝐒𝐞𝐧𝐱 𝐂𝐨𝐬𝐱 𝟏 𝐒𝐞𝐧𝐱 = 𝟐𝐒𝐞𝐜𝐱 Simplificamos. 𝟏 𝐂𝐨𝐬𝐱 + 𝟏 𝐂𝐨𝐬𝐱 𝟏 𝟏 = 𝟐𝐒𝐞𝐜𝐱
- 27. 𝟏 𝐂𝐨𝐬𝐱 + 𝟏 𝐂𝐨𝐬𝐱 = 𝟐𝐒𝐞𝐜𝐱 Sumamos lasfracciones con iguales denominadores. 𝟏 + 𝟏 𝐂𝐨𝐬𝐱 = 𝟐𝐒𝐞𝐜𝐱 𝟐 𝐂𝐨𝐬𝐱 = 𝟐𝐒𝐞𝐜𝐱 𝟐 ∗ 𝟏 𝐂𝐨𝐬𝐱 = 𝟐𝐒𝐞𝐜𝐱 𝟐 ∗ 𝐒𝐞𝐜𝐱 = 𝟐𝐒𝐞𝐜𝐱 𝟐𝐒𝐞𝐜𝐱 = 𝟐𝐒𝐞𝐜𝐱 𝐒𝐞𝐜 𝟐 𝐱𝐂𝐨𝐬𝐱 + 𝐓𝐚𝐧𝐱𝐂𝐬𝐜𝐱 ≡ 𝟐𝐒𝐞𝐜𝐱 L.Q.Q.D.
- 28. Demostrar que: (1 –Cos x)(1 + Cos x) = sen2 x Multiplicamos Distribuyendo: (1 – Cos x)(1 + Cos x) = sen2 x = Sen2 x1 + Cosx – Cosx – Cos2x 1 – Cos2x = Sen2 x Sen2 x = Sen2 x (1 – Cos x)(1 + Cos x) ≡ sen2 x L.Q.Q.D. Sen2 x