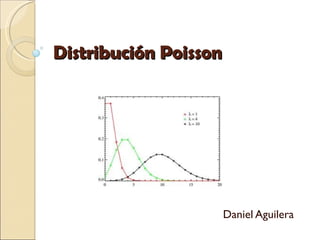
Poissonn
- 1. Distribución Poisson Daniel Aguilera
- 2. DISTRIBUCIÓN DE POISSON Fijada la extensión t del continuo, el número de fallas X (acontecimientos o resultados) que pueden encontrarse en ella es una variable aleatoria, denominada variable de POISSON, cuya media o esperanza es E( X ) = λ t = µ
- 3. DISTRIBUCIÓN DE POISSON La probabilidad de encontrar x fallas en la extensión t está dada por: p ( x; λ t ) = e − λt (λ t) x = e −µ (µ) x x! x! x = 0, 1, 2, 3, ...
- 4. EJEMPLO 4 El proceso productivo de un tipo de tela produce fallas a una tasa de 1.2 fallas cada 100 metros y se bobina en rollos de 80 metros. Definiremos como rollo de Primera Calidad aquel que tiene una falla o ninguna, de Segunda Calidad que tiene 2 fallas y de rechazo el que tiene 3 ó más fallas. Calculemos las probabilidades para cada una de estas calidades.
- 5. X: Número de fallas x = 0, 1, 2, 3, ... λ = NÚMERO MEDIO DE FALLAS UNIDAD DE EXTENSIÓN DEL CONTINUO λ = 1.2 100 = 0.012 µ = λ t = 0.012 * 80 = 0.96 p ( x; 0.96) = e −0.96 ( 0.96) x x!
- 6. p (0; 0.96) = e −0.96 ( 0.96) 0 ≅ 0.383 0! p (1; 0.96) = e −0.96 ( 0.96) ≅ 0.367 1 1! P (1a Calidad ) ≅ 0.75 P (2 a Calidad ) ≅ p (2) = 0.176 P (Re chazo) ≅ 0.074
