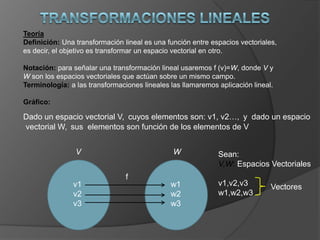
1. Teoría
Definición: Una transformación lineal es una función entre espacios vectoriales,
es decir, el objetivo es transformar un espacio vectorial en otro.
Notación: para señalar una transformación lineal usaremos f (v)=W, donde V y
W son los espacios vectoriales que actúan sobre un mismo campo.
Terminología: a las transformaciones lineales las llamaremos aplicación lineal.
Gráfico:
Dado un espacio vectorial V, cuyos elementos son: v1, v2…, y dado un espacio
vectorial W, sus elementos son función de los elementos de V
V W Sean:
V,W: Espacios Vectoriales
f
v1 w1 v1,v2,v3 Vectores
v2 w2 w1,w2,w3
v3 w3

2. Teorema:
Una función f de V en W que asigna a cada vector v , un vector f(v) Є W es
una transformación lineal, si y sólo si, α Є K, vi, vj Є V, satisface los
A A
siguientes axiomas:
1. f (vi + vj) = f (vi) + f (vj)
2. f (vi) = α.f (vi)
Teorema:
Sea f : V W Una transformación lineal, entonces se cumple que:
1. f (0v) = 0w
2. f (vi - vj) = f (vi) - f (vj)
Teorema:
Sea f : V W Una transformación lineal, dimV=n
dimV = dimN (f) + dimIm (f)

3. Ejercicios:
1. Dada la siguiente aplicación lineal, obtener la imagen de tres vectores y
realizar un diagrama.
f : P(2) R2
(a+bx+cx2 ) f (a+bx+cx2 ) = (a-b, 2c+a )
Solución:
Los vectores a considerar son: Por lo tanto, al reemplazar los valores de los
vectores, en la aplicación lineal f, obtenemos las imágenes correspondientes a cada
vector.
V1 (1-x) f (1-x) = (2,1)
2 f (3+x-2x2) = (2,-1)
V2 (3+x-2x )
2 f (0+0x+0x2) = (0,0)
V3 (0+0x+0x )
Diagrama:
P(2) R2
f
(a+bx+cx2 ) f (a+bx+cx2 ) = (y, z)

4. Ejercicios:
2. Dada la siguiente aplicación lineal, obtener la imagen de tres vectores y
realizar un diagrama.
f : R3 R2
(x, y, z ) f (x, y, z) = (2x+y+3z, -x+2y+4z)
Solución:
Los vectores a considerar son: Por lo tanto, al reemplazar los valores de los
vectores, en la aplicación lineal f, obtenemos las imágenes correspondientes a cada
vector.
V1 (1,3,2) f (1,3,2) = (11, 13)
V2 (3,5,1) f (3,5,1) = (14, 11)
V3 (0,0,0) f (0,0,0) = (0,0)
Diagrama:
R3 R2
f
(x, y, z ) f (x, y, z ) = (a, b)

5. Ejercicios:
3. Dada la siguiente aplicación lineal, obtener la imagen de tres vectores y
realizar un diagrama.
f : R3 M2 x+y-z x+3y+2z
(x, y, z ) f (x, y, z) =
2x+y-3z -3x+2y+3z
Solución:
Los vectores a considerar son: Por lo tanto, al reemplazar los valores de los
vectores, en la aplicación lineal f, obtenemos las imágenes correspondientes a cada
vector.
0 3
V1 (1,0,1) f (1,3,2) =
-1 0
0 9
V2 (-2,3,1) f (3,5,1) =
-4 15
V3 (0,0,0) f (0,0,0) = 0 0
0 0
R3 M2
Diagrama:
f a b
(x, y, z ) f (x, y, z ) =
c d

6. Teoría
Definición: El núcleo es un subespacio vectorial perteneciente al espacio
vectorial V, cuyo vector correspondiente en el espacio vectorial W es el vector
cero.
N (f) = { v Є V | f (v) = 0w }
Notación: Núcleo se denota N(f)
Gráfico:
Dado un espacio vectorial V, cuyos elementos son: v1, v2…, y dado un espacio
vectorial W, El núcleo está formado por todos aquellos vectores que tienen como
Correspondiente el vector cero en W.
V W Sean:
. V,W: Espacios Vectoriales
.
.
f v1,v5,v9
v1 Vectores
N (f) v5 0w 0w
v9
.
.
.

7. Ejercicios:
1. Dada la siguiente aplicación lineal, realice un diagrama, y escriba la definición
de núcleo.
f : R2 R3
(x, y) f (x, y) = (x-y,2x, y+x)
Solución: R3
R2
Diagrama:
f
(x, y) f (x, y) = (a, b, c)
Por la definición, y ya que el núcleo es un conjunto, lo representamos así:
N f : {x, y / f (x, y) = (x-y,2x, y+x) = (0,0,0)} Por lo tanto, planteamos nuestro sistema de
ecuaciones: Y, luego resolvemos nuestra matriz ampliada, y al resolverla, obtenemos
Las restricciones del núcleo. Finalmente expresamos el núcleo con las restricciones
reemplazadas.
x-y = 0 1 -1 0 y=0
<
N f : {(x, y)/ x = 0 y = 0}
2x = 0 2 0 0 x =0
N f : {(0, 0)}
y+x = 0 1 1 0
En este caso, el núcleo de la función es el
cero vector.

8. 2. Dada la siguiente aplicación lineal, realice un diagrama, y escriba la definición
de núcleo.
f : R2 R3
(x, y) f (x, y) = (a, a+b+c, b+c)
Solución:
P(2) R3
Diagrama:
f
(a+bx+cx2 ) f (a+bx+cx2 ) = (a, b, c)
Por la definición, y ya que el núcleo es un conjunto, lo representamos así:
N f : {a+bx+cx2 / f (a+bx+cx2) = (a, a+b+c, b+c) = (0,0,0)} Por lo tanto, planteamos el
sistema de ecuaciones: Y, luego resolvemos nuestra matriz ampliada, y al resolverla,
obtenemos las restricciones del núcleo Finalmente expresamos el núcleo con las
restricciones reemplazadas.
N f : { a+bx+cx2 / a=0
<
b= -c }
a =0 1 0 0 0 a=0 N f : { -cx+cx 2/ c Є R }
a+ b+c = 0 2 1 1 0 b+c=0 N f : { c (-x+x2) / c Є R }
b+c = 0 0 1 1 0 b=-c N f : { (-x+x2))}

9. 3. Dada la siguiente aplicación lineal, realice un diagrama, y escriba la definición
de núcleo.
x-2z 2x+y+2z
f : R3 M2
(x, y, z) f (x, y, z) =
2x+y+2z 3x+y
Solución:
Diagrama: R3 M2
f a b
(x, y, z) f (x, y, z) =
c d
Por la definición, y ya que el núcleo es un conjunto, lo representamos así:
x-2z 2x+y+2z 0 0
N f : {x, y, z / f (x, y, z) = = }
0 0
2x+y+2z 3x+y
Por lo tanto, plantemos el sistema de ecuaciones: Y, luego resolvemos nuestra matriz
ampliada, y al resolverla, obtenemos las restricciones del núcleo. Finalmente
expresamos el núcleo con las restricciones reemplazadas.
x-2z = 0 1 0 -2 0 x-2z=0 x=2z N f : {x, y, z / x=2z y=-6z }
<
2x+y+2z= 0 2 1 2 0 y+6z=0 y=-6z N f : { 2z,-6z,z / z Є R }
2x+y+2z= 0 2 1 2 0 N f : { z (2,-6,1) / z Є R }
3x+y=0 3 1 0 0 N f : {2,-6,1}