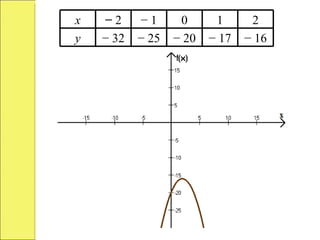
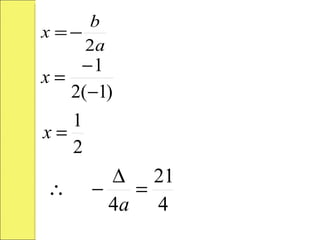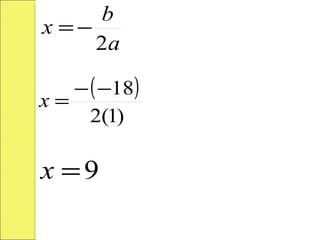El documento presenta una introducción general a la función cuadrática, incluyendo ejemplos de funciones cuadráticas, conceptos como concavidad, cortes con los ejes, vértice, intervalos de monotonía y rango. También cubre problemas de optimización relacionados con encontrar el máximo o mínimo de una función cuadrática.

1. PROF. GRETTEL ROJAS RIVERA.
FUNCIÓN CUADRÁTICA
Entrad_pes ntació1.mp3

2. ESTUDIO GENERAL DE LA
FUNCIÓN CUADRÁTICA
Ejemplos:
1) f ( x) = 2 x + 7 x − 4
2
a =2 b =7 c = −4
CONCAVIDAD:
Cóncava hacia arriba.

3. CORTES CON EL EJE X:
1 
 ,0  ∧ ( − 4,0)
2 
CORTE CON EL EJE Y:
( 0,−4)
EJE DE SIMETRÍA:
b
x=−
2a

4. − ( 7)
x=
2( 2 )
7
x=−
4
VÉRTICE
:
 b ∆
V =  − ,− 
 2a 4a 

5.  7 81 
V =  − ,− 
 4 8
INTERVALOS DE MONOTONÍA:
 b 
 − ∞, − 
 2a 
 b 
− ,+∞ 
 2a
 

6.  7
 − ∞, − 
 4
 7 
− ,+∞ 
 4
 
RANGO O ÁMBITO:
 ∆ 
A = − ,+∞ 
 4a 

7.  81 
A = − ,+∞ 
 8 
GRÁFICA:
x x1 0 b x2
−
2a
f (x ) 0 c ∆ 0
−
4a
x −4 7 0 1
−
4 2
f (x ) 0 81 − 4 0
−
8

9. 2) g ( x) = − x + 4 x − 20
2
a = −1 b = 4 c = −20
CONCAVIDAD:
Cóncava hacia abajo

10. CORTES CON EL EJE X:
No toca el eje x.
CORTE CON EL EJE Y:
( 0,−20)
EJE DE SIMETRÍA:
b
x=−
2a
4
x=−
2(−1)

11. 4
x=
2
x =2
VÉRTICE
:  b ∆
V =  − ,− 
 2a 4a 
V = ( 2,−16 )

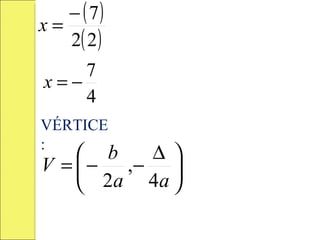
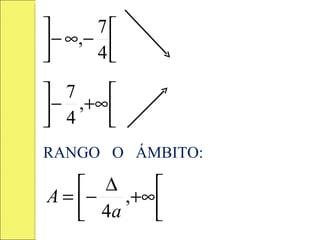
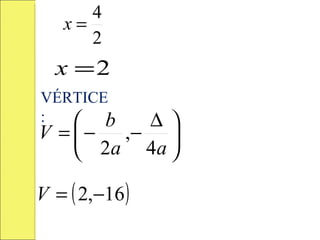
12. INTERVALOS DE MONOTONÍA:
 b 
 − ∞, − 
 2a 
 b 
− ,+∞ 
 2a
 
] − ∞,2[
] 2,+∞[

13. RANGO O ÁMBITO:
 ∆
A =  − ∞, − 
 4a 
A = ] − ∞,−16]
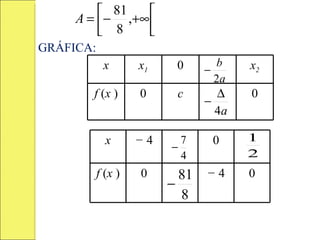
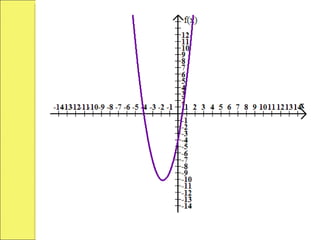
GRÁFICA:
NOTA:
Si la gráfica no toca el eje x,
entonces, para trazar la gráfica se
deben elegir números arbitrarios para
construir la tabla de valores.

14. x −2 −1 0 1 2
y − 32 − 25 − 20 − 17 − 16

15. PROBLEMAS SOBRE
OPTIMIZACIÓN
Cuando se habla de un máximo o un
mínimo en función cuadrática, se está
hablando del vértice.
El vértice es el punto
mínimo cuando es
cóncava hacia arriba.

16. El vértice es el punto
máximo cuando es
cóncava hacia abajo.
EJEMPLOS:
1) Un niño lanza una bola al aire y sigue una
trayectoria descrita por la expresión
t ( s ) = −s + s +
2
tetyetetetyeteyey 6 donde t es la posición en la
trayectoria y s es el tiempo en segundos. ¿Cuál
es la altura máxima que alcanza la bola y cuánto
tiempo tarda en lograrla?

17. b
x =−
2a
−1
x=
2(−1)
1
x=
2
∆ 21
∴ − =
4a 4

18. R/
La bola alcanza una altura máxima
de 5,25m y la logra en 0,5 segundos.
2) El costo C en dólares de producir x
cantidad de juguetes esta dado por la
relación C ( x) = x − 18 x + 100 ¿Cuál
2
es el costo mínimo de producción y
cuántos juguetes se deben producir para
alcanzarlo?

19. b
x =−
2a
− ( −18)
x=
2(1)
x =9

20. R/
El costo mínimo de producción es
de $ 19 y se alcanza produciendo 9
juguetes.