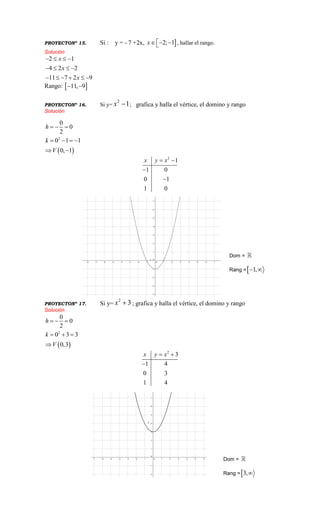
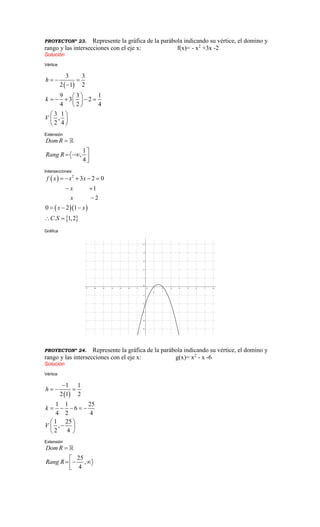
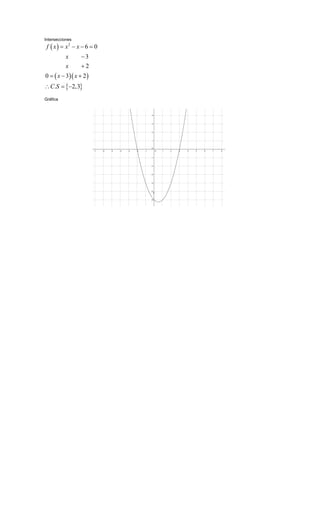
Este documento contiene 22 problemas de matemáticas relacionados con conjuntos, relaciones, funciones y gráficas. Los problemas incluyen hallar relaciones y dominios y rangos, graficar funciones cuadráticas y lineales, y determinar vértices e intersecciones.

1. MATEMATICA
PRÁCTICA CALIFICADA Nº 07
IIº AÑO DE SECUNDARIA “ ……” __________________________________
FIRMA DEL PADRE O APODERADO
19 DE MAYO DE 2016 NOMBRE: …………………………………………
Sin libros ni apuntes
NOTA: Deberás escribir las respuestas con lapicero
PROYECTONº 1. Si: (2x + 3; 3y + 8) = (y; 3+4x) Hallar: xy
Solución
 
2 3
3 8 3 4
3 2 3 8 3 4 7 11
77
x y
y x
x x x y
xy
 
  
          
 
PROYECTONº 2. Sean los conjuntos: A = {1; 2; 3; 4; 5} B = {2; 5; 7; 9; 11; 14}
Hallar la relación: R = {(x; y)  B x A / x = 3y - 1}
Solución
3 1
1 2
2 5
4 1
1
3 8
1
5 4
y y 
        2,1 ; 5,2 ; 11,4 ; 14,5R 
PROYECTONº 3. Dados los conjuntos: T = {10; 12; 14; 16; 28} y S = {3;5;7;9}.
Determinar la relación R = {(x;y) ST/ y = 3x + 1}
Solución
3 1
3 10
5
7 2
16
9 28
2
x x 
      3,10 , 5,16 , 9,28R 
PROYECTONº 4. Hallar a+b+c; si R es una relación simétrica:
R = {(4;3), (4;9), (3;b), (a+b;9), (9;c+1)}
Solución
     
     
     
4,3 3,4 3, 4
4,9 9,4 9,c 1 3
a b,9 9,a b ,9 5
12
R b b
R c
R a b a
a b c
    
     
       
   

2. PROYECTONº 5. Hallar a+b+c+d+e, si R es una relación binaria de equivalencia.
R = {(7;7), (a;a), (b;b), (7;8), (8;c), (8;9), (e; e+2),(9;7), (d;8)}
Solución
     
     
     
       
       
7,8 8,7 8,c 8
8,9 9,8 d,8 9
9,7 7,9 e,e 2 7
8,7 7,8 8,8 a,a 8
9,7 7,9 9,9 b,b 9
40
R c
R d
R e
R a
R b
a b c d e
    
    
     
     
     
     
PROYECTONº 6. Dados los conjuntos:
L = {-3; -2; 1; 4; 5}
N = {-1; -7; -3; 1; 5}
Se define la relación: R = {(x; y)  L x N / y= 2x+3}
Hallar el dominio y el rango de esta relación.
Solución
2 3
3 3
2 1
1 5
4 11
5 13
x x 
 
 
      
 
 
3, 3 , 2, 1 , 1,5
3, 2,1
3, 1,5
R
Dom R
Rang R
    
  
  
PROYECTONº 7. Si el conjunto: {(-8; a+1), (-4;b-7), (-4; 9), (-8; 10)} es una función,
indicar el valor numérico de a.b
Solución
1 10 9
7 9 16
144
a a
b b
ab
   
   
 
PROYECTONº 8. Si f(x) = 4x – 1; g(x) = 2x+13 , hallar f(g(-5))
Solución
       5 2 5 13 3 11f g f f     
PROYECTONº 9. Si: f(x) = 2x2 – 1 Hallar:
1 1
2 3
( 1) (0)
f f
E
f f
   
   
   
 
Solución
 
1 1 1 2 1 71 1
52 3 2 9 2 9
( 1) (0) 1 1 2 36
f f
E
f f
       
            
          
   
PROYECTONº 10. Si se tienen las funciones: f(x) = 8x2
- 5 ; g(x) = x3
– 3 .
Calcular: f(-2) + g(-3)
Solución
   2 3 27 30 3f g      

3. De la pregunta 11 a la 12, graficar cada una de las funciones lineales hallar el dominio
y rango
PROYECTONº 11. y = -x + 2
Solución
0 2
2 0
x y
PROYECTONº 12. y = 2x – 1 ; x  [-1;2]
Solución
1 3
2 3
x y
 
PROYECTONº 13. El vértice de la parábola y = -x2
+ 2 – 6x. es:
Solución
   
 
2
6
3
2
3 2 6 3 11
3,11
h
k
V

   

      

PROYECTONº 14. Dada la función: f(x) = bx2
+ 3x – 3
 2; 1 ,Si f hallar el valor de b  
Solución
1 4 6 3 2b b     
Dom =
Rang =
Dom =  1,2
Rang = 3,3

4. PROYECTONº 15. Si : y = - 7 +2x, 2; 1x    , hallar el rango.
Solución
2 1
4 2 2
11 7 2 9
x
x
x
   
   
     
Rango:  11, 9 
PROYECTONº 16. Si y=
2
1x  ; grafica y halla el vértice, el domino y rango
Solución
 
2
0
0
2
0 1 1
0, 1
h
k
V
  
   
 
2
1
1 0
0 1
1 0
x y x 


PROYECTONº 17. Si y=
2
3x  ; grafica y halla el vértice, el domino y rango
Solución
 
2
0
0
2
0 3 3
0,3
h
k
V
  
  

2
3
1 4
0 3
1 4
x y x 

Dom =
Rang = 1, 
Dom =
Rang =3,

5. PROYECTONº 18. Sea la función: f(x) = – x2
– 4x –
3
4
Cuya gráfica es: Halle M + N
Solución
4
2
2
3 13
4 8
4 4
5
4
M
N
M N

   

    
  
PROYECTONº 19. Halla las coordenadas del vértice de la parábola en la función
cuadrática: f(x)= -x2
- 4x + 8
Solución
 
4
2
2
4 8 8 12
2,12
h
k
V

   

    

PROYECTONº 20. Determina las coordenadas del vértice y los puntos de corte con el eje x en la
función cuadrática : f(x)= 2x2
- 4x - 6
Solución
Vértice
 
4
2
2
4 8 8 12
2,12
h
k
V

   

    

Intersecciones
   
  
 
2
2 2 3 0
3
1
0 2 3 1
. 1,3
f x x x
x
x
x x
C S
   


  
  

6. PROYECTONº 21. Determina las coordenadas del vértice y los puntos de corte con el eje x en la
función cuadrática : f(x)= 3x2
-7x - 6
Solución
Vértice
 
7 7
2 3 6
49 7 121
3 7 6
36 6 12
7 121
,
6 12
h
k
V

  
   
       
   
 
 
 
Intersecciones
 
  
2
3 7 6 0
3 2
3
0 3 2 3
2
. ,3
3
f x x x
x
x
x x
C S
   


  
 
   
 
PROYECTONº 22. Represente la gráfica de la parábola indicando su vértice, el domino y
rango y las intersecciones con el eje x : f(x)= x2
- 2x – 3
Solución
Vértice
 
 
2
2
1
2
1 2 1 3 4
1, 4
h
k
V

  
    

Extensión
 4,
Dom R
Rang R

  
Intersecciones
 
  
 
2
2 3 0
3
1
0 3 1
. 1,3
f x x x
x
x
x x
C S
   


  
  
Gráfica

7. PROYECTONº 23. Represente la gráfica de la parábola indicando su vértice, el domino y
rango y las intersecciones con el eje x: f(x)= - x2
+3x -2
Solución
Vértice
 
3 3
2 1 2
9 3 1
3 2
4 2 4
3 1
,
2 4
h
k
V
  

 
     
 
 
 
 
Extensión
1
,
4
Dom R
Rang R


  
Intersecciones
 
  
 
2
3 2 0
1
2
0 2 1
. 1,2
f x x x
x
x
x x
C S
    
 

  
 
Gráfica
PROYECTONº 24. Represente la gráfica de la parábola indicando su vértice, el domino y
rango y las intersecciones con el eje x: g(x)= x2
- x -6
Solución
Vértice
 
1 1
2 1 2
1 1 25
6
4 2 4
1 25
,
2 4
h
k
V

  
    
 
 
 
Extensión
25
,
4
Dom R
Rang R


  

8. Intersecciones
 
  
 
2
6 0
3
2
0 3 2
. 2,3
f x x x
x
x
x x
C S
   


  
  
Gráfica