Simetria impar

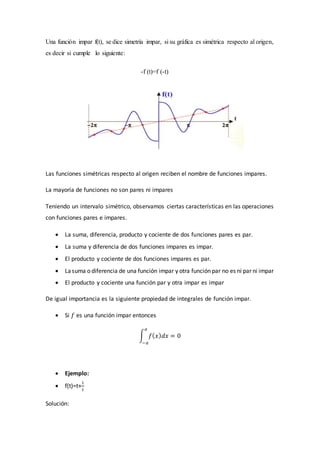
1. Una función impar f(t), se dice simetría impar, si su gráfica es simétrica respecto al origen,
es decir si cumple lo siguiente:
-f (t)=f (-t)
Las funciones simétricas respecto al origen reciben el nombre de funciones impares.
La mayoría de funciones no son pares ni impares
Teniendo un intervalo simétrico, observamos ciertas características en las operaciones
con funciones pares e impares.
 La suma, diferencia, producto y cociente de dos funciones pares es par.
 La suma y diferencia de dos funciones impares es impar.
 El producto y cociente de dos funciones impares es par.
 Lasuma o diferencia de una función impar y otra función par no es ni par ni impar
 El producto y cociente una función par y otra impar es impar
De igual importancia es la siguiente propiedad de integrales de función impar.
 Si 𝑓 es una función impar entonces
∫ 𝑓( 𝑥) 𝑑𝑥 = 0
𝑎
−𝑎
 Ejemplo:
 f(t)=t+
1
𝑡
Solución:

2. Como f(−t) = −t −
1
𝑡
= −f(t)
Por tanto f(t) es función impar
 Determinar si 𝑓( 𝑥) = 𝑥3
es función par o impar.
𝑓(−𝑥) = (−𝑥3
)
𝑓(−𝑥) = −𝑥3
𝑓(−𝑥) = −𝑓(𝑥), la función es impar
Serie de Fourier de senos “𝒇(𝒙) funcion impar”
Es extender el comportamiento de una función definida en medio de intervalos como a
una función impar.
La serie de Fourier de una función impar en el intervalo (−𝑝, 𝑝) es la serie de senos.
𝑎0 = 0
𝑎 𝑛 = 0
𝑏 𝑛 =
2
𝑝
∫ 𝑓( 𝑥) 𝑠𝑒𝑛 (
𝑛𝜋
𝑝
) 𝑥 𝑑𝑥
𝑝
0
Una función se puede decir que es impar, sí cuando tomamos un período de la función,
lo giramos en el eje Y y luego en el eje X, este coincide exactamente con otro período de
la función.
Como la función 𝑠𝑒𝑛(𝑛𝜔0 𝑡) es una funcion impar para tod 𝑛 ≠ 0, es de esperar que:
Si 𝑓(𝑡) es impar, su surie de Fourier no contendrá términos coseno, por lo tanto 𝑎 𝑛 = 0
para todo 𝑛.
Por ejemplo, la señal cuadrada, ya analizada en un ejemplo anterior previo:

3. Es una función impar, por ello su serie de Fourier no contiene términos coseno:
𝑓( 𝑡) =
4
𝜋
[𝑠𝑒𝑛( 𝜔0 𝑡) +
1
3
𝑠𝑒𝑛(3𝜔0 𝑡) +
1
5
𝑠𝑒𝑛(5𝜔0 𝑡) + ⋯]
Simetría Coeficientes Funciones en la serie
Impar 𝑎 𝑛 = 0
𝑏 𝑛 =
4
𝑇
∫ 𝑓( 𝑡) 𝑠𝑒𝑛(𝑛𝜔0 𝑡)𝑑𝑡
𝑇/2
0
Únicamente senos
Ejemplos:
 𝑓( 𝑥) = 3𝑥 − 𝑥3
𝑓(−𝑥) = 3(−𝑥)− (−𝑥3)
= −(3𝑥 − 𝑥3)
= −𝑓(𝑥)
 𝑓( 𝑥) = 𝑥5
+ 𝑥3
− 𝑥
𝑓(−𝑥) = (−𝑥)5
+ (−𝑥)3
− (−𝑥)
= −𝑥5
− 𝑥3
+ 𝑥
= −𝑓(𝑥)

4.  𝑓( 𝑥) =
𝑥
1−𝑥2
𝑓(−𝑥) =
(−𝑥)
1 − (−𝑥)2
= −
−𝑥
1 − 𝑥2
= −𝑓(𝑥)