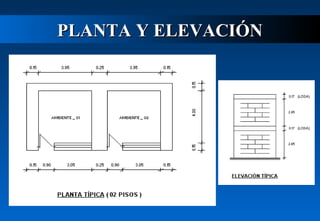
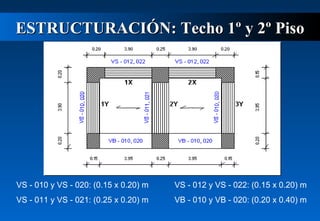
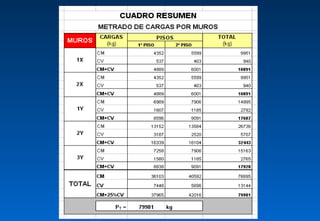
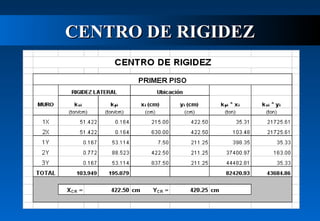
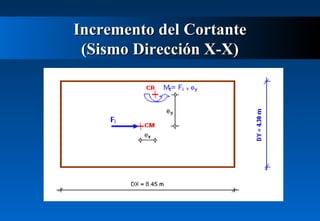
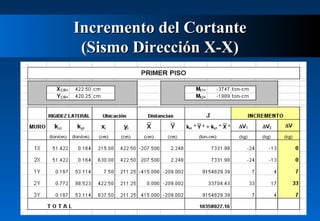
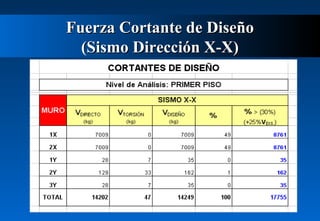
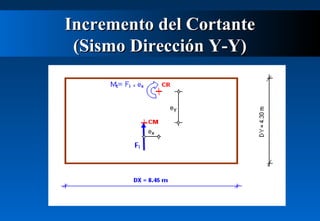
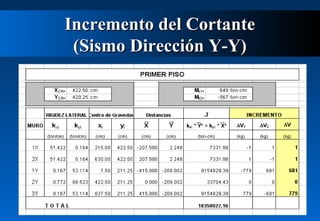
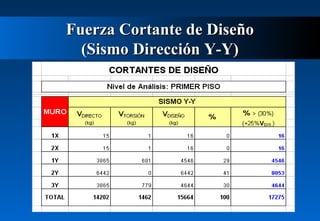
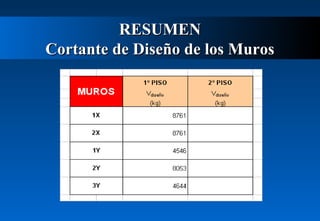
Este documento describe cómo calcular la fuerza cortante debida a la torsión en un edificio de dos pisos. Explica cómo determinar los centros de masa y rigidez de cada piso, y cómo una excentricidad entre estos centros produce un momento torsor que incrementa el cortante en los muros. Luego calcula las excentricidades reales y accidentales del primer piso y usa estas para determinar los momentos torsores y el incremento resultante en el cortante debido a la torsión para ambas direcciones del sismo. Finalmente presenta el cortante de

1. FUERZA CORTANTE
DEBIDO A LA TORSIÓN
Ing. Ronald Santana Tapia
UAP – Facultad de Ingeniería Civil

2. PLANTA Y ELEVACIÓN

3. DATOS GENERALES
Datos generales:
Resistencia a la compresión: f’m = 25 kg/cm²
Módulo de elasticidad: Em = 500 * f’m
Altura de piso a techo: h = 2.45 m
Espesor de losa aligerada: elosa = 0.17 m
Mortero: Tipo P1 (Mortero Sin Cal)
Datos de diseño:
f’c = 175 kg/cm²
fy = 4200 kg/cm²

4. ESTRUCTURACIÓN: Techo 1º y 2º Piso
VS - 010 y VS - 020: (0.15 x 0.20) m
VS - 012 y VS - 022: (0.15 x 0.20) m
VS - 011 y VS - 021: (0.25 x 0.20) m
VB - 010 y VB - 020: (0.20 x 0.40) m

6. CENTRO DE MASA
CENTRO DE MASA: (XCM, YCM)
El centro de masa para cada piso se determina tomando
en cuenta los muros estructurales y no estructurales.
XCM = ∑ Pi * xi
∑ Pi
YCM = ∑ Pi * yi
∑ Pi
Pi : Carga de gravedad que soporta el muro “i”.
(CM + CV)
xi, yi : Ubicación de cada muro respecto a un sistema de
ejes referenciales.

7. CENTRO DE MASA

8. CENTRO DE RIGIDEZ
CENTRO DE RIGIDEZ: (XCR, YCR)
El centro de rigidez para cada piso se determina respecto
a un sistema de coordenadas referencial X-Y, mediante la
siguiente expresión:
XCR = ∑ kyi * xi
∑ kyi
YCR = ∑ kxi * yi
∑ kxi
Kxi : Rigidez lateral del muro “i” en la dirección “X”
Kyi : Rigidez lateral del muro “i” en la dirección “Y”
xi, yi : Ubicación de cada muro respecto a un sistema de
ejes referenciales.

9. CENTRO DE RIGIDEZ

10. FUERZA CORTANTE DEBIDO A LA
TORSIÓN
Si el centro de masa no coincide con el centro de rigidez se origina
una excentricidad real, produciéndose un momento torsor el cuál
produce un incremento en los cortantes de los muros de
albañilería, estos incrementos deben ser considerados para
efectos de diseño.
Asimismo, se considerará una excentricidad accidental
perpendicular a la dirección del sismo igual a 0.05 veces la
dimensión del edificio en la dirección perpendicular a la dirección
de análisis.

11. Incremento del Cortante
(Sismo Dirección X-X)

12. Incremento del Cortante
(Sismo Dirección X-X)
EXCENTRICIDADES: (Primer Piso)
Excentricidad real
:
ey = yCM – yCR = e
e = 258.68 – 420.25 = -161.57 cm
Excentr. accidental
:
eacc = 0.05 Dy
eacc = 0.05 * 430 = 21.5 cm

13. Incremento del Cortante
(Sismo Dirección X-X)
MOMENTOS TORSORES:
En cada nivel además de la fuerza cortante directa, se aplicará el
momento torsor bajo dos condiciones siguientes:
Condición 1
:
Mti_1 = Vi (1.5 e + eacc)
Condición 2
:
Mti_2 = Vi (e – eacc)
En donde:
Vi = Fuerza cortante en el nivel “i”.

14. Incremento del Cortante
(Sismo Dirección X-X)
Primer Piso:
Condición 1:
Mti_1 = Vi (1.5 e + eacc)
Mti_1 = 14,202 (1.5* -161.57 - 21.5) = -3747 ton-cm
Condición 2:
Mti_2 = Vi (e – eacc)
Mti_2 = 14,202 (-161.57 + 21.5) = -1989 ton-cm

15. Incremento del Cortante
(Sismo Dirección X-X)
INCREMENTO DEL CORTANTE POR TORSIÓN:
Condición 1:
ΔV1 = Mti_1 * Kxi . Y
J
Condición 2:
ΔV2 = Mti_2 * Kxi . Y
J
En donde:
X = Xi – XCR
Y = Yi – YCR
J = Σkyi . X ² + Σkxi . Y ²

16. Incremento del Cortante
(Sismo Dirección X-X)

17. Fuerza Cortante de Diseño
(Sismo Dirección X-X)

18. Incremento del Cortante
(Sismo Dirección Y-Y)

19. Incremento del Cortante
(Sismo Dirección Y-Y)
EXCENTRICIDADES: (Primer Piso)
Excentricidad real
:
ex = xCM – xCR = e
e = 424.80 – 422.50 = 2.30 cm
Excentr. accidental
:
eacc = 0.05 Dx
eacc = 0.05 * 845 = 42.25 cm

20. Incremento del Cortante
(Sismo Dirección Y-Y)
MOMENTOS TORSORES: (Primer Piso)
Condición 1:
Mti_1 = Vi (1.5 e + eacc)
Mti_1 = 14,202 (1.5* 2.30 + 42.25) = 649 ton-cm.
Condición 2:
Mti_2 = Vi (e – eacc)
Mti_2 = 14,202 (2.30 – 42.25) = -567 ton-cm

21. Incremento del Cortante
(Sismo Dirección Y-Y)
INCREMENTO DEL CORTANTE POR TORSIÓN:
Condición 1:
ΔV1 = Mti_1 * Kyi . X
J
Condición 2:
ΔV2 = Mti_2 * Kyi . X
J
En donde:
X = Xi – XCR
Y = Yi – YCR
J = Σkyi . X ² + Σkxi . Y ²

22. Incremento del Cortante
(Sismo Dirección Y-Y)

23. Fuerza Cortante de Diseño
(Sismo Dirección Y-Y)

24. RESUMEN
Cortante de Diseño de los Muros