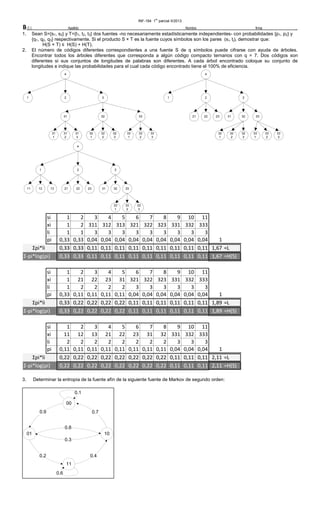
Este documento presenta tres problemas relacionados con la teoría de la información: 1) Demostrar que la entropía de la fuente producto de dos fuentes es menor o igual a la suma de las entropías individuales. 2) Encontrar todos los árboles de códigos compactos ternarios posibles para una fuente de 7 símbolos y calcular su eficiencia. 3) Calcular la entropía de la fuente afín asociada a una fuente de Markov de segundo orden dada.

1. INF-164 1
er
parcial II/2013
A C.I. Apellido Nombre firma _
So poi
0 p
1 q
Fuente
Original
S pi
000 ppp
001 ppq
010 pqp
011 pqq
100 qpp
101 qpq
110 qqp
111 qqq
Tercera
extensión
T pi
0 qqq
1 3pqq
2 3ppq
3 ppp
Fuente T
1. Sean S={s1, s2, s3} y T={t1, t2} dos fuentes -no necesariamente estadísticamente independientes- con probabilidades {p1, p2, p3}
y {q1, q2} respectivamente. Si el producto S × T es la fuente cuyos símbolos son los pares (si, tj), demostrar que:
H(S × T) ≤ H(S) + H(T).
   
)()()()()|(
)()/(
)(log)()|(log)()(log)()|()|(log)()|(
)(log)|(log)()|()()|(log)()|()(
THSHTSHSHTSHcomo
THTSH
tPtPtsPtPtPtPtsPtsPtPtsP
tPtsPtPtsPtPtsPtPtsPTSH
i
jj
i j
jij
i j
jjji
i j
jijji
i j
jjijji
i j
jjijji






2. Sea S la extensión de tercer orden de una fuente binaria de memoria nula, cuya probabilidad de emitir un 0 es igual a p. Otra
fuente, T, observa las salidas de S, emitiendo un 0, 1, 2 ó 3 según que la salida de S contenga 0,1,2 ó 3 ceros.
a) (10) Calcular H(S)
b) (15) Calcular H(T)
c) (05) Interpretar el resultado de H(S) – H(T).
3
3
2
2
2
2
3
3 1
log
1
log3
1
log3
1
log)(
q
q
pq
pq
qp
qp
p
pSH 
3
3
2
2
2
2
3
3 1
log
3
1
log3
3
1
log3
1
log)(
q
q
pq
pq
qp
qp
p
pTH 
)()()3log(3)()3log(3)3(log3)3(log3)()( 2222
THSHpqpqqppqqpTHSH 
3. Determinar la entropía de la fuente afín de la siguiente fuente de Markov de segundo orden
0.3
0.9
0.8 0.4
0.2
0.7
01
11
00
10
0.6
0.1
1,56
1/13
3/13
3/13
6/13
= 4/13
= 9/13
0,89049
p(1)=p(1/00)p(00)+p(1/10)p(10)+p(1/01)p(01)+p(1/11)p(11) = w2 + w4
p(00) = w1 = p13p34 / D =
p(01) = w2 = p34p21 / D =
Entropia de la Fuente Afin S'
H( S' ) =
p(10) = w3 = p34p21 / D =
p(11) = w4 = p42p21 / D =
D = p34p13+ 2p21p34 + p42 p21 =
p(0)=p(0/00)p(00)+p(0/10)p(10)+p(0/01)p(01)+p(0/11)p(11) = w1 + w3
1 31 1 1
2 2 21 3
3 3 32 4
4 4 42 4
1 2 3 4
1 3
0.1 0.0 0.3 0.00.1 0 0.3 0
0.9 0.0 0.7 0.00.9 0 0.7 0
0 0.8 0 0.4 0.0 0.8 0.0 0.4
0 0.2 0 0.6 0.0 0.2 0.0 0.6
1
0.9 0.0 0.3 0
w ww w w
w w ww w
w w ww w
w w ww w
w w w w
w w
       
                
            
   
    1
31 3
1 2 3 2 3
2 3 4
1
22 42 4
1 1 1
3 3 61 2 3 4 1 2 3 4 1
3 3 61
13 13 13 131 1 1 1 1 1 2 3 4
.0 0
0.9 0.7 0.0 0
00.0 0.2 0.4
00.0 0.8 0.0 0.4
3 ; 6
3 3 6 1 13 1 ; ; ;
w w
w w w w w
w w w
w ww w
w w w w w w w w w
w w w w w w w w w

    
  
   
       
          
0,1 0,0 0,3 0,0 0,077 0,077
0,9 0,0 0,7 0,0 0,231 0,231
0,0 0,8 0,0 0,4 0,231 0,369
0,0 0,2 0,0 0,6 0,462 0,323
X =

2. INF-164 1
er
parcial II/2013
B C.I. Apellido Nombre firma _
1. Sean S={s1, s2} y T={t1, t2, t3} dos fuentes -no necesariamente estadísticamente independientes- con probabilidades {p1, p2} y
{q1, q2, q3} respectivamente. Si el producto S × T es la fuente cuyos símbolos son los pares (si, tj), demostrar que:
H(S × T) ≤ H(S) + H(T).
2. El número de códigos diferentes correspondientes a una fuente S de q símbolos puede cifrarse con ayuda de árboles.
Encontrar todos los árboles diferentes que corresponda a algún código compacto ternarios con q = 7. Dos códigos son
diferentes si sus conjuntos de longitudes de palabras son diferentes. A cada árbol encontrado coloque su conjunto de
longitudes e indique las probabilidades para el cual cada código encontrado tiene el 100% de eficiencia.
e
31
1 2 3
3332
33
1
33
3
33
2
32
1
32
3
32
2
31
1
31
3
31
2
e
31
1 2 3
333222
33
1
33
3
33
2
32
1
32
3
32
2
21 23
e
31
2 3
333222
33
1
33
3
33
2
21 23
1
1211 13
si 1 2 3 4 5 6 7 8 9 10 11
xi 1 2 311 312 313 321 322 323 331 332 333
li 1 1 3 3 3 3 3 3 3 3 3
pi 0,33 0,33 0,04 0,04 0,04 0,04 0,04 0,04 0,04 0,04 0,04 1
Σpi*li 0,33 0,33 0,11 0,11 0,11 0,11 0,11 0,11 0,11 0,11 0,11 1,67 =L
Σ-pi*log(pi) 0,33 0,33 0,11 0,11 0,11 0,11 0,11 0,11 0,11 0,11 0,11 1,67 =H(S)
si 1 2 3 4 5 6 7 8 9 10 11
xi 1 21 22 23 31 321 322 323 331 332 333
li 1 2 2 2 2 3 3 3 3 3 3
pi 0,33 0,11 0,11 0,11 0,11 0,04 0,04 0,04 0,04 0,04 0,04 1
Σpi*li 0,33 0,22 0,22 0,22 0,22 0,11 0,11 0,11 0,11 0,11 0,11 1,89 =L
Σ-pi*log(pi) 0,33 0,22 0,22 0,22 0,22 0,11 0,11 0,11 0,11 0,11 0,11 1,89 =H(S)
si 1 2 3 4 5 6 7 8 9 10 11
xi 11 12 13 21 22 23 31 32 331 332 333
li 2 2 2 2 2 2 2 2 3 3 3
pi 0,11 0,11 0,11 0,11 0,11 0,11 0,11 0,11 0,04 0,04 0,04 1
Σpi*li 0,22 0,22 0,22 0,22 0,22 0,22 0,22 0,22 0,11 0,11 0,11 2,11 =L
Σ-pi*log(pi) 0,22 0,22 0,22 0,22 0,22 0,22 0,22 0,22 0,11 0,11 0,11 2,11 =H(S)
3. Determinar la entropía de la fuente afín de la siguiente fuente de Markov de segundo orden:
0.70.9
0.2 0.4
0.8
0.3
01
11
00
10
0.6
0.1