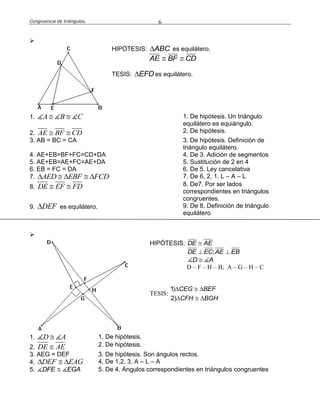
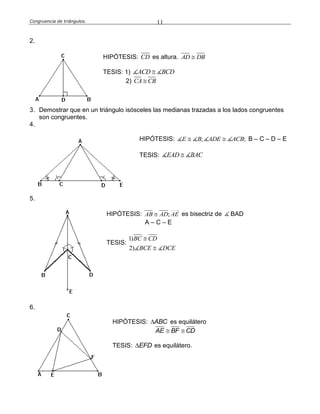
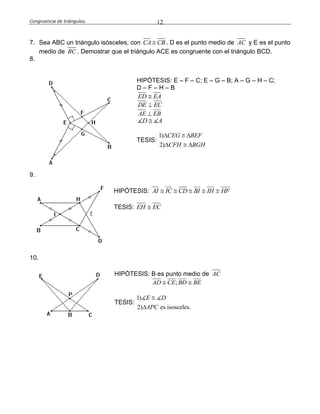
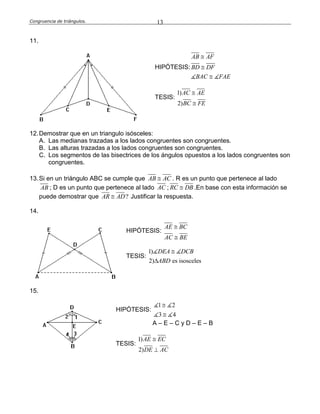
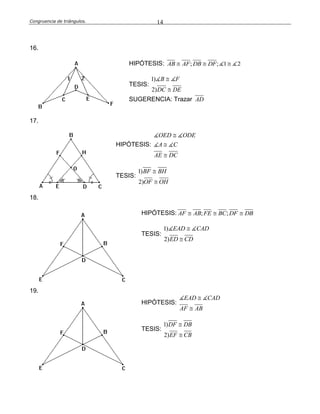
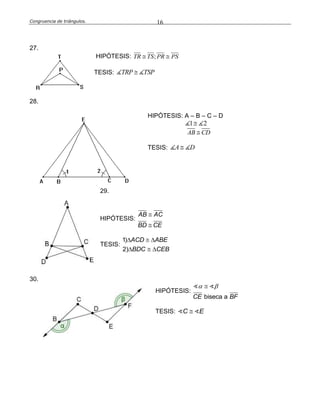
Este documento define la congruencia de triángulos y presenta varios teoremas relacionados. La congruencia de triángulos ocurre cuando dos triángulos tienen los mismos lados y ángulos. Se presentan tres teoremas clave: el teorema L-A-L (lado-ángulo-lado), el teorema A-L-A (ángulo-lado-ángulo) y el teorema L-L-L (lado-lado-lado). Finalmente, se resuelven varios ejercicios como ejemplos de aplicación