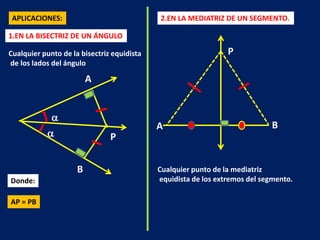
Este documento describe las condiciones para que dos triángulos sean congruentes y resuelve problemas aplicando estas condiciones. Existen tres casos suficientes para la congruencia de triángulos: 1) ángulo-lado-ángulo, 2) lado-ángulo-lado, y 3) lado-lado-lado. El documento también explica conceptos como bisectriz, mediatriz y base media, y cómo aplicarlos para resolver problemas geométricos.

1. DOCENTE: CORNEJO PEÑALOZA, Víctor
CONGRUENCIA DE
TRIÁNGULOS

2. 1.Concepto: dos triángulos son congruentes si sus lados respectivos y los ángulos
opuestos a dichos lados son congruentes.
A
B
C
P
Q
R
Entonces podemos afirmar:
Por lo tanto:
ABC PQR
AB PQ
AC PR
BC QR
m A m P  
m B m Q  
m C m R  

3. 2.CONDICINES SUFICIENTES PARA LA CONGRUENCIA DE TRIÁNGULOS
CASO: ángulo – lado – ángulo ( A L A )
Son congruentes un lado y los ángulos adyacentes.
a aq q
AC MN
m A m N  
m C m M  
CONDICIONES SUFICIENTES PARA LA CONGRUENCIA DE TRIÁNGULOS.

4. CASO: lado – ángulo – lado ( L A L )
Si son congruentes dos lados y el ángulo comprendido entre ellos.
A
B
S N
T
C
b b
AB ST
AC SN
m A m S  

5. CASO: lado – lado – lado ( L L L )
Si son congruentes los tres lados.

6. Problemas resueltos:
1.Hallar el valor de “x”
Desarrollo:
Estamos en caso LAL los triángulos
Son congruentes
entonces a ángulos iguales se oponen
Lados iguales.
X + 5 = 12
X = 7
2.En la figura encuentra el valor de «a»

7. Desarrollo:
Si observamos estamos en un caso, ALA. Los
triángulos son congruentes.
A ángulos iguales se oponen lados
iguales.
a = 12
3.En la figura, halla «a + b»
Desarrollo:
Se observa que hay dos
ángulos congruentes y un
Lado común entre ellos.

8. Caso: ALA.
A ángulos congruente
lados iguales.
A + b
10 + 4 =14
4.En la figura AM = BC
Halla : MBC

9. Desarrollo:
x
x73°
107°
107°
N
De la figura se observa que el triángulo ANM es congruente con el triángulo
BMC.
Caso: LAL
Resolviendo en el triángulo BMC se tiene:
X = 39°

10. 5.En la figura halla MB
Desarrollo:
45°
a
a b
b
45m C  
El triángulo ABC es isósceles.
Observando la figura ( ALA) :
AMB CRB
MB = 8

12. Conocimiento previo:
DISTANCIA ENTRE DE UN PUNTO
( P ) A UNA RECTA .
L
P
d
Es la longitud ( d) de la perpendicular
Trazada del punto ( P ) a la recta.
DISTANCIA DE UN PUNTO ( Q ) A UN
SEGMENTO ( AB)
A B
Q
d
L
Es la longitud ( d ) de la perpendicular
al segmento o a su prolongación.
MEDIATRIZ DE UN SEGMENTO
La mediatriz es una recta ( L ) perpendicular
que pasa por el punto medio del segmento
( AB )
A B
L

13. APLICACIONES:
1.EN LA BISECTRIZ DE UN ÁNGULO
Cualquier punto de la bisectriz equidista
de los lados del ángulo
a
a
A
B
P
Donde:
AP = PB
2.EN LA MEDIATRIZ DE UN SEGMENTO.
A B
P
Cualquier punto de la mediatriz
equidista de los extremos del segmento.

14. 3.EN UN TRIÁNGULO ISÓSCELES
En todo triángulo isósceles la bisectriz del ángulo desigual es la altura, mediana y se
encuentra contenida en la mediatriz.
M
q
q

15. BASE MEDIA
Es el segmento que une los puntos medios
de dos lados de un triángulo es paralelo y
mide la mitad de su longitud y se lo
denomina base media.
//MN AC
2
AC
MN 
En un triángulo la base media genera
4 triángulos congruentes.

16. Ejemplos:
1.En la figura ABCD es un cuadrado,
BH = 3m y DF = 5m .Halla HF
Desarrollo:
3
5
a
a
5
3
Los triángulos rectángulos tienen igual hipotenusa
y ángulos agudos iguales. ( ALA )
AH = 5 + 3 = 8 m

17. 2.En la figura halla «x» si HB = HC.
Desarrollo:
Por propiedad de la bisectriz de un
ángulo se tiene que:
X = 20°
3. En la figura L es mediatriz y AB = MC
Halla «x»

18. desarrollo
55°
Los triángulos AMH y MHC son
congruentes ( mediatriz de un
segmento)
55°
el triángulo ABM es isósceles.
X = 70°
H
A C
M

19. 4.En un triángulo ABC se ubican P , Q y M
los puntos medios de AB , BC y AC.
Si PQ // AC Y 70m PMQ  
Desarrollo:
A
B
C
M
P
Q
70°
Halla m PBQ
por propiedad de base media:
X = 70°