Este documento presenta las funciones hiperbólicas y sus inversas. Define las funciones hiperbólicas senh, cosh, tanh, csch, sech y coth y sus dominios e identidades. También define las funciones hiperbólicas inversas senh-1, cosh-1, tanh-1, csch-1, sech-1 y coth-1 y explica cómo se pueden expresar en términos de funciones logarítmicas. Presenta ejemplos para calcular valores y verificar identidades de las funciones hiperbólicas

1. 2.3 Funciones hiperbólicas y sus inversas.
Competencia: Realizar cálculos donde se involucren funciones hiperbólicas y funciones
hiperbólicas inversas, mediante la utilización de sus propiedades e identidades.
Las funciones hiperbólicas están definidas en base a funciones exponenciales.
Definición 2.3.1: Funciones hiperbólicas:
a) d)
b) c)
d) e)
 Ejemplo 2.3.1: Encuentra el valor indicado utilizando tres cifras decimales.
a) senh(2) b) cosh(-1) c) tanh(3)

2. Al igual que las funciones trigonométricas, las funciones hiperbólicas tienen una serie de
entidades entre ellas que permiten convertir valores de una función hiperbólica a otra.
Identidades hiperbólicas:
a) g)
b) h)
c) i)
d) j)
e) k)
f)
 Ejemplo 2.3.2: Si conocemos que senh(x)=2. Calcula el resto de las funciones hiperbólicas
inversas. Si el resultado no es racional utiliza tres cifras decimales.
 Ejemplo 2.3.3: Verifica que la identidad hiperbólica a) es verdadera:
cosh2 ( x)  senh2 ( x)  1 .
 Ejemplo 2.3.4: Considera la gráfica de la función f(x) = csch(x) que se muestra para obtener
los siguientes valores:
a) csch(a)
b) senh[csch(
b)]
c) cosh[csch(
c)]

3. Ahora revisemos las funciones hiperbólicas inversas en base a las funciones
hiperbólicas originales y a las generalidades de las funciones inversas.
Recordatorio: ¿Qué se tiene que cumplir para afirmar que una función g(x) es la inversa de
la función f(x)?
a) .
b) .
c) .
d) .
La respuesta es el inciso d).
Recordatorio: Para que la inversa de una función f(x) exista en un intervalo dado, se requiere
que sea inyectiva. ¿Qué significa esto?
a) Que la función sea siempre creciente o siempre decreciente en el intervalo.
b) Que la función sea creciente y decreciente en el intervalo.
c) Que la función sea siempre positiva en el intervalo.
d) Que la función sea siempre negativa en el intervalo.
La respuesta es el inciso a).
 Ejemplo 2.3.5: En base a sus gráficas, identifica qué funciones hiperbólicas tienen función
inversa.

4. Solución:
 Se observa que la gráfica de la función seno hiperbólico es siempre creciente, por lo tanto
su función inversa existe.
 La función coseno hiperbólico es decreciente a la izquierda del eje vertical, y después es
creciente, por lo que su función inversa no existe, al menos en lo que respecta a su
definición original.
 La función tangente hiperbólico es siempre creciente, por lo que su función inversa existe.
 La función cosecante hiperbólico siempre es decreciente, por lo que su función inversa sí
existe.
 La gráfica de la función secante hiperbólico indica que primero es creciente y después del
eje vertical se vuelve decreciente, por lo que su inversa no existe, al menos en lo que
respecta a su función original.
 Finalmente, se observa que la función cotangente hiperbólico siempre es decreciente, por
lo tanto su función inversa sí existe.
En el ejemplo anterior se llegó a la conclusión de que las funciones coseno hiperbólico y
secante hiperbólico no eran inyectivas para todo su dominio, por lo que sus funciones inversas
no existen. Ahora revisemos estas mismas funciones pero con su dominio acotado para
números reales: [0, ).

5. Con la acotación propuesta, se observa que las funciones son siempre creciente para el
caso de la función secante hiperbólico, y siempre decreciente, para el caso de la función
cosecante hiperbólico, por lo que para estas funciones acotadas, también existen funciones
inversas.

6. Recordatorio: ¿Qué característica guarda la gráfica de la inversa de una función con
respecto a la gráfica de la función original?
a) Es un reflejo de la función tomando como referencia el eje horizontal.
b) Es un reflejo de la función tomando como referencia el eje vertical.
c) Es un reflejo de la función tomando como referencia la recta y = x.
d) Es idéntica a la función original.
La respuesta es el inciso c).
Si las funciones hiperbólicas están definidas en base a funciones exponenciales naturales, es
de esperarse que las funciones hiperbólicas inversas se puedan expresar en términos de
funciones logarítmicas naturales.
 Ejemplo 2.3.6: Las gráficas que se muestran a continuación corresponden a las seis
funciones hiperbólicas inversas. Identifícalas.
Definición 2.3.2: Funciones hiperbólicas inversas:
Función Dominio Rango
a) (-, ) (-, )
b) [1, ) [0, )
c) (-1, 1) (-, )
d) (-, -1)  (1, ) (-, 0)  (0, )
e) (0, 1] [0, )
f) (-, 0)  (0, ) (-, 0)  (0, )

7. a) b) c)
d) e) f)
Solución:
Para identificar las gráficas de las funciones hiperbólicas inversas recurrimos a las gráficas de
las funciones hiperbólicas que se muestran en la
definición 2.3.1
a) Corresponde al reflejo con respecto al eje y = x
de la función tangente hiperbólico, por lo tanto se
trata de la función tanh-1(x).

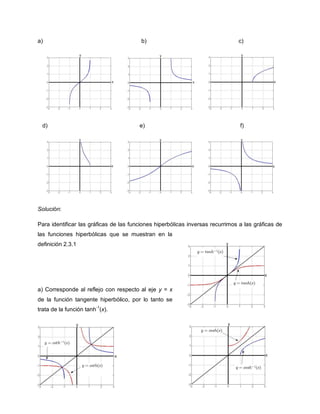
8. b) Corresponde al reflejo con respecto al eje y = x de la función cotangente hiperbólico, por lo
tanto se trata de la función coth-1(x).
c) En este caso se trata del reflejo con respecto al eje y = x de la función coseno hiperbólico,
por lo tanto se trata de la función cosh-1(x).
d) El reflejo de esta función con respecto al eje y = x
corresponde al secante hiperbólico, por lo tanto se trata de
la función sech-1(x).
e) Corresponde al reflejo con respecto al eje y = x de la
función seno hiperbólico, por lo tanto se trata de la
función senh-1(x).
f) Esta función es el reflejo con respecto al eje y = x del
cosecante hiperbólico, por lo tanto se trata de la función
csch-1(x).
 Ejemplo 2.3.7: Considera las definiciones de las funciones seno hiperbólico y seno
hiperbólico inverso para verificar que se cumple que senh senh 1 ( x)]  x .
[

9.  Ejemplo 2.3.8: Considera las gráficas de las funciones seno hiperbólico y coseno hiperbólico
inverso que se muestran para determinar los valores indicados. Se pide que sólo utilices las
gráficas para encontrar los valores.
a) senh(1) b) senh-1(-3) c) senh-1(-1)
d) cosh-1[senh(1.44)] e) cosh-1[senh-1(1.18)]
Solución:
En este caso las respuestas se obtendrán sólo de las gráficas, por lo que será necesario
reafirmar las siguientes consideraciones:
 Para la gráfica del seno hiperbólico, la coordenada y corresponde al seno hiperbólico
inverso de la coordenada x correspondiente.
 Para la misma gráfica del seno hiperbólico, la coordenada x corresponde al seno
hiperbólico inverso de la coordenada y correspondiente.
 Para la gráfica del coseno hiperbólico inverso, la coordenada y corresponde al coseno
hiperbólico inverso de la coordenada x correspondiente.
 Para la misma gráfica del coseno hiperbólico inverso, la coordenada x corresponde al
coseno hiperbólico de la coordenada y correspondiente.
a) La respuesta se obtiene al observar la gráfica de la función seno hiperbólico y corresponde
al valor de la coordenada y en la gráfica para el cual su coordenada x es 1.
senh(1) =
b) y c) En este caso también la gráfica de la función seno hiperbólico sirve para encontrar el

10. resultado, y corresponde al valor de la coordenada x en la gráfica cuya coordenada y es -3.
senh-1(-3) =
senh-1(-1) =
d) Primero se utiliza la gráfica del seno hiperbólico determinando la coordenada y
correspondiente y posteriormente la gráfica del coseno hiperbólico inverso:
cosh-1[senh(1.44)] = cosh-1[2] =
e) Con la gráfica del seno hiperbólico se encuentra el valor del senh-1(1.18) y posteriormente se
utiliza este valor en la gráfica del coseno hiperbólico inverso:
cosh-1[senh-1(1.18)] = cosh-1[1] =
NOTA: Se recomienda utilizar una calculadora para comprobar los valores obtenidos de las gráficas.