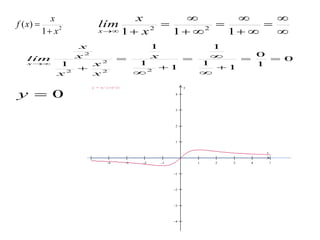
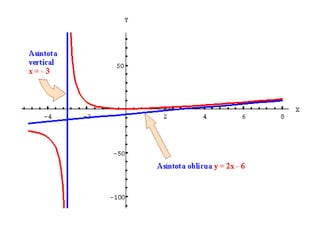
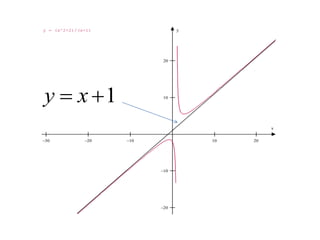
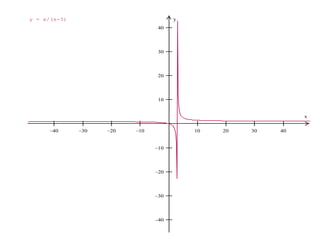
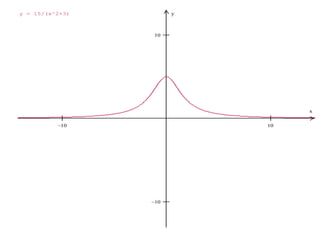
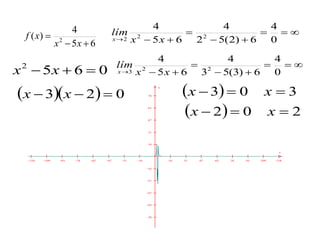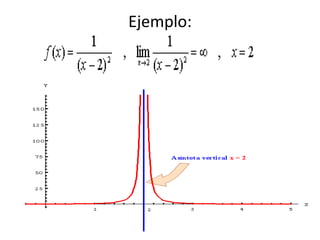
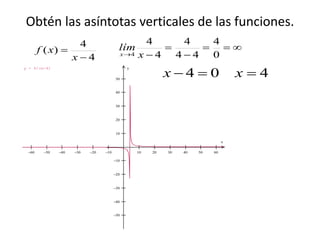
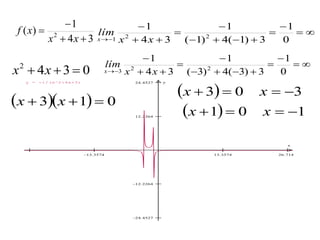
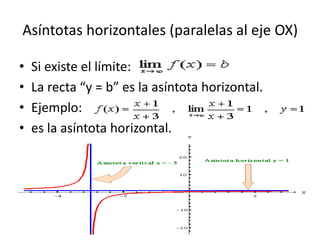
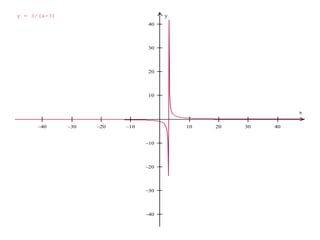
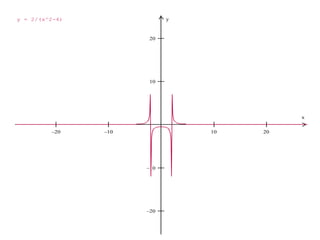
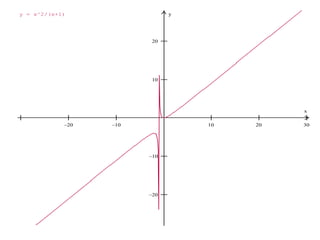
1. Una asíntota es una recta a la que una función se aproxima indefinidamente pero nunca la alcanza cuando una de sus variables tiende al infinito. Existen asíntotas verticales y horizontales. 2. Las asíntotas verticales ocurren en funciones racionales cuando el denominador es igual a cero, mientras que las asíntotas horizontales ocurren cuando el límite del cociente de los polinomios del numerador y denominador tiende a un valor constante. 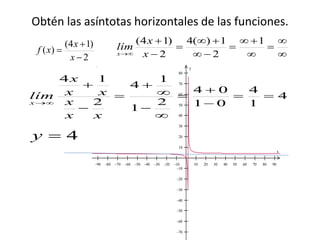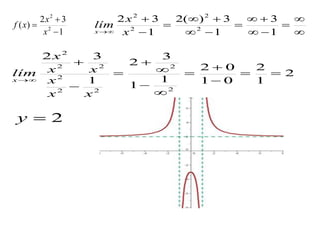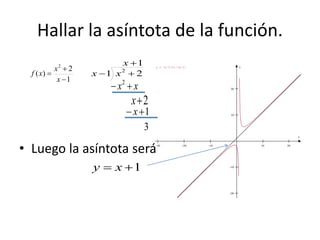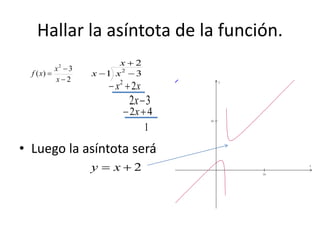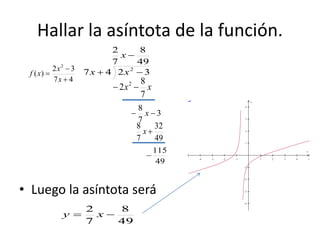3. El documento proporciona ejemplos de cómo calcular las asíntotas

1. Asíntotas.

2. ASÍNTOTAS DE UNA FUNCIÓN.
• Las asíntotas son rectas a las cuales la función se va
aproximando indefinidamente, cuando por lo menos
una de las variables (x o y) tienden al infinito.
• Una definición más formal es:
• DEFINICIÓN
• Si un punto (x, y) se desplaza continuamente por una
función y=f(x) de tal forma que, por lo menos, una de
sus coordenadas tienda al infinito, mientras que la
distancia entre ese punto y una recta determinada
tiende a cero, esta recta recibe el nombre de asíntota
de la función.

3. Las asíntotas se clasifican en:

4. Asíntotas.
• Definición:
• Una asíntota es una recta que se encuentra
asociada a la gráfica de algunas curvas y que se
comporta como un límite gráfico hacia la cual la
gráfica se aproxima indefinidamente pero nunca
la toca y mucho menos la brinca. A medida que la
variable independiente de la función tiende a un
cierto valor, la correspondiente variable
dependiente tiende a infinito, cualquiera que este
sea.

5. Asíntotas verticales.
• Como su nombre lo índica, son rectas verticales
asociadas a la función. Se encuentran presentes
únicamente en funciones racionales de la forma:
y se determinan encontrando las raíces del
denominador P(x) correspondiente.
Tales valores reciben el nombre de Polos de la
función. Entonces, el número de polos asociados
a una función determinan el número de asíntotas
verticales que tiene la función.
)(
)(
)(
xQ
xP
xf 

6. • Asíntotas verticales (paralelas al eje OY)
• Si existe un número “a” tal, que :
• La recta “x = a” es la asíntota vertical.

7. Ejemplo:

8. Obtén las asíntotas verticales de las funciones.
4
4
)(


x
xf 


 0
4
44
4
4
4
4 x
lím
x
404  xx
           










x
yy = 4/(x-4)

9. 65
4
)( 2


xx
xf 


 0
4
6)2(52
4
65
4
222 xx
lím
x



 0
4
6)3(53
4
65
4
223 xx
lím
x0652
 xx
   023  xx   303  xx
  202  xx
               










x
y

10. 34
1
)( 2



xx
xf 







 0
1
3)1(4)1(
1
34
1
221 xx
lím
x








 0
1
3)3(4)3(
1
34
1
223 xx
lím
x0342
 xx
   013  xx
  303  xx
  101  xx
  




x
yy = -1/(x^2+4x+3)

11. Determina las asíntotas verticales de las siguientes funciones
1
32
)( 2
2



x
x
xf
1
4
)(
2



x
xx
xf
42
63
)(



x
x
xf

12. Asíntotas horizontales.
• Como su nombre lo indica, son rectas
horizontales asociadas a la función. Se
encuentran presentes únicamente en funciones
racionales de la forma.
• Y se determinan haciendo que la variable
independiente “x”, tienda al infinito lo que trae
como consecuencia que la función cociente
tienda a un valor determinado fijo, al que nunca
va a llegar y mucho menos sobrepasar
)(
)(
)(
xQ
xP
xf 

13. • Dependiendo de la relación entre los grados
de los polinomios, tendremos los siguientes
caso:
1. El polinomio P(x) del numerador y el
polinomio Q(x) del denominador tienen el
mismo grado.
 La asíntota horizontal es la recta dada por el
cociente de los coeficientes de grado mayor.
)(
)(
)(
xQ
xP
xf 

14. 2. El grado del polinomio Q(x) del denominador
es mayor que el grado del polinomio P(x) del
numerador.
 En estos casos la asíntota es la recta y=0.
3. El grado del polinomio Q(x) del denominador
es menor que el grado del polinomio P(x) del
numerador.
 En este caso no hay asíntota horizontal.

15. TEOREMA:
• Sea F una función racional definida por el
cociente de dos polinomios:
• Entonces:
1. Para n < m, la recta y = 0 (el eje x) es una
asíntota horizontal.
2. Para n = m, la recta , es una asíntota
horizontal.
3. Para n > m, no hay asíntotas horizontales.
0
1
1
0
1
1
...
...
)(
)(
)(
bxbxb
axaxa
xQ
xP
xf m
m
m
m
n
n
n
n


 



m
n
b
a
y 

16. Asíntotas horizontales (paralelas al eje OX)
• Si existe el límite:
• La recta “y = b” es la asíntota horizontal.
• Ejemplo:
• es la asíntota horizontal.

17. Obtén las asíntotas horizontales de las funciones.
2
)14(
)(



x
x
xf 











1
2
1)(4
2
)14(
x
x
lím
x
4y
4
1
4
01
04
2
1
1
4
2
14












xx
x
xx
x
lím
x
                 















x
y

18. 1
32
)( 2
2



x
x
xf











 1
3
1
3)(2
1
32
2
2
2
2
x
x
lím
x
2
1
2
01
02
1
1
3
2
1
32
2
2
22
2
22
2












xx
x
xx
x
lím
x
2y

19. 2
1
)(
x
x
xf











 111 22
x
x
lím
x
0
1
0
1
1
1
1
1
1
1
22
2
2
2









x
x
x
x
x
x
lím
x
0y
        








x
yy = x/(1+x^2)

20. 2
4
1
)(
x
x
xf













111
2
4
2
4
x
x
lím
x
existeno
x
x
xx
x
lím
x
0
1
0
01
1
1
1
1
1
1
1
2
4
4
2
44
4













• Por lo tanto no tiene asíntotas horizontales.
                     




















x
yy = (x^4+1)/x^2

21. Calcular las asíntotas horizontales de las funciones:
2
2
)(
2



x
x
xf
2
1
)(
x
x
xf


1
23
)( 2
2



x
xx
xf
32
1
)(



x
x
xf
6
32
)( 2
2



x
xx
xf
1
1
5)( 2


x
xf

22. Asíntotas oblicuas.
• Si el grado del numerador de una función
racional es mayor en una unidad que el grado
del denominador, la función (gráfica) tiene
una asíntota oblicua (inclinada). Las asíntotas
oblicuas de una función son rectas oblicuas, es
decir, rectas de la forma . Una función
puede tener, como máximo, dos asíntotas
oblicuas distintas (una por la izquierda de su
gráfica y otra por la derecha de la misma).
nmxy 

23. • Nota-1
• Las asíntotas horizontales y oblicuas son
excluyentes, es decir la existencia de unas,
implica la no existencia de las otras.
• Nota-2
• En el cálculo de los límites se entiende la
posibilidad de calcular los límites laterales
(derecho, izquierdo), pudiendo dar lugar a la
existencia de asíntotas por la derecha y por la
izquierda diferentes o solo una de las dos.

24. Métodos para calcular las asíntotas oblicuas.
• Para que existan asíntotas oblicuas será
preciso que la función tenga denominador. El
cálculo de dichas asíntotas se podrá realizar
por alguno de los dos métodos siguientes:

25. 1er método:
• Sea una función
• Para hallar la asíntota oblicua, se dividirá
el numerador entre el denominador y el
cociente será la asíntota buscada, es decir.
)(
)(
)(
xQ
xP
xf 
nmx
xpxQ

)()(
R
asíntota
siduoRe

26. Hallar la asíntota de la función.
• Luego la asíntota será
1
2
)(
2



x
x
xf
1
21 2


x
xx
xx  2
2x
1x
3
1 xy
    




x
yy = (x^2+2)/(x-1)

27. Hallar la asíntota de la función.
• Luego la asíntota será
2
3
)(
2



x
x
xf
2
31 2


x
xx
xx 22

32 x
42  x
1
2 xy 

x
y

28. Hallar la asíntota de la función.
• Luego la asíntota será
47
32
)(
2



x
x
xf
49
8
7
2
3247 2


x
xx
xx
7
8
2 2

3
7
8
 x
49
32
7
8
x
49
115

49
8
7
2
 xy
        








x
y

29. 2do. Método:
• El segundo método consiste en hallar las
constantes m y n de la ecuación de la asíntota
oblicua:
donde m se calcula mediante el límite:
y n con el límite
nmxy 
x
xf
límm
x
)(


))(( mxxflímn
x



30. Asíntotas oblicuas (inclinadas)
• Si existen los límites:
• La recta “y = mx+n” es la asíntota oblicua.
• Ejemplo:
• es la asíntota oblicua.

32. Ejemplo:
1
2
)(
2



x
x
xf
x
x
x
límm
x
1
22




)1(
22



 xx
x
límm
x
xx
x
límm
x 


 2
2
2






 2
2
2
x
límm 2
2
22
2
22
2
1
1
2
1
1
2
x
x
xx
x
xx
x
límm
x







1
01
01
1
1
2
1
1
1
2
1
2
2
2
2













x
xlímm
x
1m

33. 










x
x
x
límn
x 1
22
 mxxflímn
x


)(









 1
)1(22
x
xxx
límn
x









 1
)2 22
x
xxx
límn
x 1
2



 x
x
límn
x 





 1
2
x
límn
x
x
xx
x
x
x
xlímn
x 1
1
1
2
1
2






 1
1
1
01
10
1
1
1
2
1
1
1
2












x
xlímn
x
1n 1 xy
oblicuaasíntota

34.     




x
yy = (x^2+2)/(x-1)
1 xy

35. Hallar las asíntotas oblicuas de las siguientes funciones:
32
2
)( 2
23



xx
xx
xf
2
32
)(
2



x
xx
xf
13
32
)( 2
2



x
x
xf
1
2
)(
2


x
x
xf
42
3
)(
2



x
x
xf

36.        








x
yy = x/(x-3)

37.  


x
yy = 15/(x^2+3)

38.        








x
yy = 3/(x-3)

39.    




x
yy = 2/(x^2-4)

40.     




x
yy = x^2/(x+1)