Este documento presenta el contenido didáctico del curso de Termodinámica de la Universidad Nacional Abierta y a Distancia de Colombia (UNAD). Explica que el curso cubre dos unidades divididas en seis capítulos y treinta lecciones sobre conceptos básicos de termodinámica. Además, describe la estructura de cada lección, incluyendo objetivos, contenidos, ejemplos y actividades de autoevaluación. Finalmente, incluye un índice del contenido de las dos unidades que comprenden temas como la ley cero





























































































































![UNIVERSIDAD NACIONAL ABIERTA Y A DISTANCIA – UNAD
ESCUELA DE CIENCIAS BÁSICAS, TECNOLOGÍA E INGENIERÍA
CONTENIDO DIDÁCTICO DEL CURSO: 201015 – TERMODINÁMICA
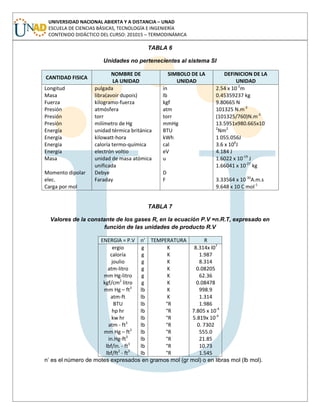
SOLUCIÓN DEL PROBLEMA
Reacción balanceada CaC2(s) + 2H2O(l)
25 ºC, 1 atm
Ca(OH)2(s) + C2H2(g)
0000
)( )(2)(2)(22)(2 2 lSgS OHfCaCfHCfOHCaf
o
R HHHHH
Entalpía de productos Entalpía de reactantes
Remplazando por los correspondientes valores
o
RH [1mol(-235,58kcal/mol) + 1mol(54,19kcal/mol)] - [1mol(-14,8) + 2mol(-68,32kcal/mol)]
o
RH [-181,39 kcal] – [-151,44 kcal] = -29,95 kcal/mol
El signo negativo indica que se trata de una reacción exotérmica.
Ejemplo 28
Calcular el calor producido cuando, en un calorímetro
a 25 ºC y 1 atm, reaccionan 2,50 g de zinc con
suficiente ácido clorhídrico. Los calores de formación
del ácido clorhídrico y del cloruro de zinc en solución
son respectivamente -39,85 y -115,54 kcal/mol
Figura 58: Datos ejemplo 28
ANÁLISIS DEL PROBLEMA](https://image.slidesharecdn.com/52976486-201015-termodinamica-modulo-150118193453-conversion-gate02/85/52976486-201015-termodinamica-modulo-127-320.jpg)
![UNIVERSIDAD NACIONAL ABIERTA Y A DISTANCIA – UNAD
ESCUELA DE CIENCIAS BÁSICAS, TECNOLOGÍA E INGENIERÍA
CONTENIDO DIDÁCTICO DEL CURSO: 201015 – TERMODINÁMICA
Al reaccionar el zinc con una solución de ácido clorhídrico se produce cloruro de zinc en
solución e hidrógeno gaseoso. Para determinar la cantidad de calor producida se debe en
primer lugar escribir la ecuación balanceada correspondiente y evaluar el cambio de
entalpía por mol de zinc y luego determinar el calor producido al reaccionar los moles que
corresponden a 2,50 g de zinc. Recuerde que las entalpías molares de los elementos a
condiciones normales son cero.
SOLUCIÓN DEL PROBLEMA
Reacción Zn(s) + 2HCl(sln) ZnCl2(sln) + H2(g)
0000
ln)()()(2ln)(2 2 ssgs ClHfZnHZnClf
o
R HHHHH
Las entalpías molares del hidrógeno y del zinc son cero, remplazando se tiene
o
RH [1mol(-115,54kcal/mol)] – [2mol(-39,85kcal/mol)]
o
RH -35,84 kcal
El signo negativo indica que se trata de una reacción exotérmica.
Calor Normal de Combustión
El calor normal de combustión se define como el cambio de entalpía durante la reacción
de oxidación completa de 1 mol de un compuesto orgánico para formar como productos
CO2(g) y H2O(l) a condiciones normales. Si la sustancia además de carbono, hidrógeno y
oxígeno contiene nitrógeno, azufre o un halógeno se obtendrán como productos N2(g),
SO2(g) y HX ( sln). Recuerde que X representa cualquier halógeno como cloro, bromo o
yodo.
El calor de normal de combustión para un mol de un compuesto orgánico se representa
mediante
o
CH y su valor se puede determinar experimentalmente utilizando calorímetros
diseñados para este fin. Los valores de los calores de combustión de las sustancias
orgánicas se pueden utilizar para calcular los correspondientes calores normales de
formación que por reacción directa es imposible su determinación experimental. A
continuación se ilustra como a partir de conocer el calor de combustión de cualquier
hidrocarburo se puede determinar su calor normal de formación:
La reacción general de combustión de un hidrocarburo se representa mediante la
siguiente ecuación:](https://image.slidesharecdn.com/52976486-201015-termodinamica-modulo-150118193453-conversion-gate02/85/52976486-201015-termodinamica-modulo-128-320.jpg)










![UNIVERSIDAD NACIONAL ABIERTA Y A DISTANCIA – UNAD
ESCUELA DE CIENCIAS BÁSICAS, TECNOLOGÍA E INGENIERÍA
CONTENIDO DIDÁCTICO DEL CURSO: 201015 – TERMODINÁMICA
ANÁLISIS DEL PROBLEMA
Como se estudió en la sección anterior, es necesario calcular primero el calor de
reacción a las condiciones estándares y luego realizar la integración correspondiente
como lo sugiere la ecuación 156. La primera parte de la integración corresponde a la
sumatoria de las ecuaciones para las capacidades caloríficas molares de los productos,
en este caso para el CO2. La segunda parte corresponde a la sumatoria de las
ecuaciones para las capacidades caloríficas molares de los reactantes, CO y O2. En
ambas partes se deben considerar los coeficientes que tienen las sustancias en la
ecuación química.
SOLUCIÓN DEL PROBLEMA
)/42,26()/05,94()( )()(2298 molkcalmolkcalHHH gg CO
o
fCO
o
f
o
R
molkcalH o
R /63,67)( 298
dTCn
dTCndTCnCn
j
iji
react
o
pj
prod
o
pireact
o
pjprod
o
pi
773
298
)(
773
298
)(
773
298
)()(
)(
)()(
6,094.5)10415,31014,10339,6()(
773
298
263
773
298
)( dTTxTxdTCn iprod
o
pi
dTTxTx
TxTxdTCn jreact
o
pj
)]10005,110167,3117,6(
)102675,010811,1350,6[()(
263
2
1
773
298
263
773
298
)(
Al resolver esta integral utilizando para ello una hoja de cálculo o calculadora se obtiene](https://image.slidesharecdn.com/52976486-201015-termodinamica-modulo-150118193453-conversion-gate02/85/52976486-201015-termodinamica-modulo-139-320.jpg)