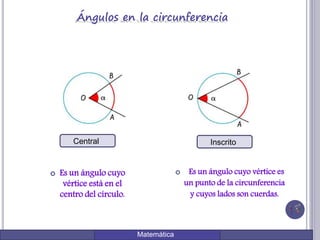
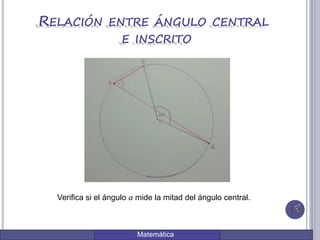
El documento describe una actividad para comprobar la relación entre el ángulo central y el ángulo inscrito en una circunferencia. Se dibuja una circunferencia y un ángulo central de 60 grados. Luego se trazan las cuerdas desde un punto C en la circunferencia hasta los extremos del arco central, formando un ángulo inscrito de 30 grados. Esto verifica que el ángulo central mide el doble que el ángulo inscrito.

1. Geometría
Objetivo: Comprobar la relaciónentre el ángulo interior y el
inscrito conmaterial concreto

2. Ángulos en la circunferencia
Central Inscrito
Matemática
 Es un ángulo cuyo
vértice está en el
centro del círculo.
 Es un ángulo cuyo vértice es
un punto de la circunferencia
y cuyos lados son cuerdas.

3. Matemática
MATERIALES
• Hojas de block o blancas
• Compas
• Transportador
• Lápices de distinto color
• Regla

4. Matemática
RELACIÓN ENTRE ÁNGULO CENTRAL
E INSCRITO
Dibujamos una circunferencia con el compás

5. Matemática
RELACIÓN ENTRE ÁNGULO CENTRAL
E INSCRITO
Construimos un ángulo con el transportador, el cual debe
tener su vértice en el centro de la circunferencia

6. Matemática
RELACIÓN ENTRE ÁNGULO CENTRAL
E INSCRITO
El ejemplo tendrá una medida de 60°, además se nombran
los puntos con letras mayúsculas

7. Matemática
RELACIÓN ENTRE ÁNGULO CENTRAL
E INSCRITO
Luego a cualquier punto sobre la circunferencia lo
nombramos C. y desde ese puntos trazamos las cuerdas
BC y AC. Formando un ángulo inscrito

8. Matemática
RELACIÓN ENTRE ÁNGULO CENTRAL
E INSCRITO
Con el transportador medimos el ángulo inscrito que se formo en el vértice
C, el cual será 30°.
Con lo cual queda comprobado que el ángulo central mide el doble que el
inscrito

9. Matemática
RELACIÓN ENTRE ÁNGULO CENTRAL
E INSCRITO
Verifica si el ángulo 𝛼 mide la mitad del ángulo central.

10. Matemática