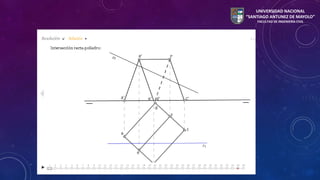
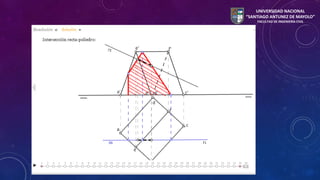
Este documento presenta información sobre poliedros e intersecciones de sólidos. Introduce los poliedros regulares e irregulares, describiendo sus elementos constituyentes como caras, aristas y vértices. Explica cómo localizar puntos en caras de prisma y pirámide usando planos cortantes, y cómo determinar la intersección entre un volumen y una línea trazando la sección plana creada por el plano cortante.