Aproximacion_Interpolacion.doc

UNIVERSIDAD NACIONAL EXPERIMENTAL
“FRANCISCO DE MIRANDA”
DEPARTAMENTO DE FISICA Y MATEMÁTICA
Licda. ALEXANDRA NOGUERA, MSc © UNEFM 2011
Pág. Nº 1
UNIDAD III: APROXIMACIÓN E INTERPOLACIÓN
APROXIMACIONES MEDIANTE LA SERIE DE TAYLOR
El Teorema de Taylor es una herramienta fundamental,útil y necesaria para el desarrollo yla comprensión de la mayoría de
los métodos numéricos que vamos a estudiar.
Si P es una función polinómica
P(x)=ao+a1x+…+anxn
Entonces P(x) puede calcularse fácilmente cualquiera sea el número x.Pero la mayoría de las funciones matemáticas no se
pueden evaluar en términos de las operaciones elementales aritméticas, por ejemplo: f(x) = Cos x ó f(x)= Ln x, las cuales
no pueden ser evaluadas sin el uso de una calculadora o mejor aún, de una computadora.
Para poder evaluar este tipo de funciones usamos funciones f*(x) casi iguales a f(x), que son fáciles de evaluar. Las f*(x)
más comunes son los polinomios dentro de los cuales se encuentran los Polinomios de Taylor como los más utilizados.
Dada la función f(x)=ex
ó Cos x, construimos un polinomio de Taylor lineal P1(x) que imite el comportamiento de la función
f(x) en algún punto x=a del dominio y sea casi igual a los puntos cercanos a x=a.
P1(x)= b1 + b2(x-a)
Para determinar los coeficientes b1 y b2 de manera única en el punto x=a, hacemos:
P1(a)= f(a)
P1´(a)= f ´(a) (1)
Por lo que se puede verificar que el polinomio tiene una única
forma:
P1(x)= f(a)+(x-a)f ´(a) (2)
Por lo que la gráfica de y= P1(x) es tangente a aquella de y= f(x) en
x=a. tal y como se muestra en la Gráfica 1.
Gráfica 1
CONCLUSION: (2) es un Polinomio de Taylor de orden 1 en x=a para aproximar a f(x) por medio de la Tangente.
EJEMPLOS:
1.- Encuentre P1(x) en a=1 para f(x)=Ln x y úselo para calcular valores aproximados de Ln(0,9) y Ln(1,5).
Solución:
Como: P1(x)=f(a)+f ´(a)(x-a)
Debemos encontrar f(a) y luego, calcular la primera
derivada de f(x) y evaluarla en a=1 para posteriormente
sustituirla en la fórmula de P1(x).
f(a)=Ln a f(1)=Ln(1) = 0
1
1
1
1
)
´(
1
)
´( 




a
a
f
x
x
f
Sustituyendo los valores encontrados en P1(x) tenemos
P1(x)=0+1(x-a)  P1(x)= (x-1)
Entonces usamos P1(x) para calcular valores aproximados
de Ln(0,9) y Ln(1,5).
P1(0,9) = 0,9-1 = -0,1 Ln(0,9) = -0,1053
P1(1,5)= 1,5-1 = 0,5 Ln(1,5) = 0,4054
En conclusion: Ln x  (x-1)
Gráfica 2
1
-1
y=x-1
y=Ln(x)
x=a
f(a) (a,f(a))
y=f(x) y=P1(x)

Pág. Nº 2
Obtención de un Polinomio de Taylor de Orden 2.-
En general, podemos aproximar a f(x) en x=a a polinomios que cumplan con las condiciones siguientes:
Pn
(j)(a) = f(j)(a) con j=1,2,..,n
donde: f(j)(x) es la j-ésima derivada de f(x) en x=a. Entonces:
Rn(x) es el resto probable de la serie cuya fórmula para su cálculo es:
donde z es un número entre a y x ( se llama residuo después de n +1 términos.)
OBSERVACION: La serie de Taylor se rebautizará "serie de Maclaurin" para x = 0
Fórmulas y series de Taylor de funciones elementales
Observe que f(x) = ex
es una función que puede derivarse infinitamente (derivadas de cualquier orden).Tomemos este caso
para desarrollar Polinomios de Taylor para a = 0 ( a en este caso vale cero ). En este caso estudiaremos a f(a) y sus
derivadas en a para sustituirlas en la fórmula polinomial Pn(x)
f(0) = e0
= 1
f’(0) = e0
= 1
f"(0) = e0
= 1, ....
f n
(0) = e0
= 1,
f n+1
(z) = ez
(0 < z < x)
al sustituir estos valores en Pn(x) tenemos:
Rn
a
x
n
a
f
a
x
a
f
a
x
a
f
a
x
a
f
a
f
x
P n
n
n 









 )
(
!
)
(
...
)
(
!
3
)
´´´(
)
(
!
2
)
´´(
)
(
!
1
)
´(
)
(
)
( 3
2
1
3
2
)
0
(
)!
1
(
)
0
(
!
1
...
)
0
(
!
3
1
)
0
(
!
2
1
)
0
(
!
1
1
1
)
( 












 n
z
n
n x
n
e
x
n
x
x
x
x
P
)!
1
(
!
...
6
2
1
)
(
1
3
2









n
x
e
n
x
x
x
x
x
P
n
z
n
n
EJEMPLO:
Supongamos que deseamos aproximarnos al valor de ex para x = 1 usando Polinomios de Taylor con n = 6
(grado 6º ). En este caso tenemos:
71806
,
2
720
1
120
1
24
1
6
1
2
1
2
!
6
1
!
5
1
!
4
1
!
3
1
!
2
1
1
1
)
1
(
6
5
4
3
2
6 













P
Para hallar el error utilizaremos el resto,
)!
1
(
1



n
x
e
R
n
z
n
Tengamos en cuenta que e0 = 1 y e1 = 2,71828, así que ex < 3 (es el límite,por lo que suplantaremos ez por 3 )
Conviene tomar en cuenta que, como tenemos 6 términos para hallar el resto utilizaremos el séptimo,n = 7, asíque:

Pág. Nº 3
(lo cual es un error menor a 0,001)
EJERCICIOS PROPUESTOS
1. Úsese los términos en la serie de Taylor de cero a cuarto orden para aproximar la función f(x)=-
0.1x4
-0.15x3
-0.5x2
-0.25x+1.2 desde xi=0 con h=1. Esto es predecir el valor de la función en xi+1=1.
Evalúe los errores verdaderos en cada aproximación.
2. Use los términos del polinomio de Taylor con n=0 hasta 6 para aproximar f(x)=Cos x en
3


x con base al valor
de f(x) y sus derivadas en
4


a .Obsérvese que esto significa que
12
4
3
)
(







 a
x
h . Evalúe los
errores en cada aproximación.
3. Use los términos de la serie de Taylor de cero a tercer orden para predecir f(2) para: f(x)=25x3
-6x2
+7x-88
4. Use los términos de la serie de Taylor de cero al cuarto orden para estimar f(3) para f(x)=Ln x, usando como punto
de base a=1.Calcule el error relativo porcentual en cada aproximación y analice los resultados.
INTERPOLACIÓN
Una de las funciones más útiles y bondadosas son los polinomios ya que estas son fáciles de derivar y de
integrar (indefinidas) además los resultados son también polinomios.
La expresión P(x) = a0 + a1x + a2x2 + . . . + an-1xn-1 + anxn con an  0, representa un polinomio entero en x de
grado n(entero no negativo) y a0, a1, . . . ,an son constantes reales o complejas.
Una razón de su importancia es que aproximan uniformemente funciones continuas. Dada cualquier función
definida y continua en un intervalo cerrado, existe un polinomio que se encuentra tan “cerca” de la función como
se desea. Este resultado se expresa en el siguiente
TEOREMA: Aproximación de Weierstrass
Si f es definida y continua en [a, b] y dado  >0, existe entonces un polinomio P, definido en [a, b] tal que: f(x)
– P(x)< , para todo x en el intervalo [a, b].
f(x) + ,
P(x)
f (x)
f(x) - ,
a b
Interpolación Polinómica. Fórmula de Lagrange. Diferencias Divididas. Fórmula de Interpolación de
Newton.
El proceso de ajustar una serie de datos de una tabla de valores o de una función dada a una curva es lo que
se denomina interpolación. Este proceso también sirve para estimar valores intermedios entre datos precisos.

Pág. Nº 4
Definición: Una función de interpolación es aquella que pasa a través de puntos dados como datos de una
tabla de valores o puntos de una curva.
La interpolación polinomial consiste en ajustar un polinomio a los puntos dados de una tabla.
Aunque existe uno y sólo un polinomio de n-ésimo orden que se ajusta a los n + 1 puntos, existen una gran
variedad de fórmulas matemáticas mediante las cuales se puede expresar este polinomio. En esta unidad se
estudian dos técnicas alternativas que están bien condicionadas para implementarse en una computadora.
Estos son los polinomios de Newton y de Lagrange.
Sea f una función y xo, x1, ..., xn, n+1 puntos diferentes en los cuales se puede evaluar f; se determinará un
polinomio de grado  n tal que: P(xo) = f(xo), P(x1) = f(x1), . . ., P(xn) = f(xn)
Los problemas en los cuales interviene la interpolación son:
 Extensión de tablas de valores con argumentos que no están en ella.
 Para encontrar la gráfica de funciones suaves no oscilantes exactas o aproximadas.
 Evaluar funciones trascendentales.
 Diferenciar e integrar numéricamente.
(a) Interpolación de polinomios de Lagrange
Interpolación Lineal: El método más sencillo de interpolación es conectar dos puntos con una línea recta,
esta técnica se llama interpolación lineal. La forma de Lagrange para una línea recta que pasa por los
puntos (x0, y0) y (x1, y1) es:
P(x) =
 
 
 
  1
0
1
0
0
1
0
1
y
x
x
x
x
y
x
x
x
x





;
es fácil verificar que esta expresión representa la ecuación de una línea recta y que los puntos dados
pertenecen a ella.
La fórmula de Lagrange de la ecuación de la parábola que pasa por los puntos (x0, y0), (x1, y1) y (x2, y2)
es: P(x) =
  
  
  
  
  
   2
1
0
0
2
1
0
1
2
1
0
1
0
0
2
0
1
0
1
y
x
x
x
x
x
x
x
x
y
x
x
x
x
x
x
x
x
y
x
x
x
x
x
x
x
x














.
Esta se denomina interpolación cuadrática.
La fórmula general del polinomio de Interpolación de Lagrange de grado a lo sumo n, que pasa a través de
los puntos (x0, y0), (x1, y1),. . . , (xn, yn) tal que P(x0) = y0, . . . , P(xn) = yn y tiene la forma:
P(x) = L0y0 + L1y1 + . . . + Lnyn.
Siendo Lk =
 
       
       
k
j
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
n
k
k
k
k
k
k
k
n
k
k
n
j j
k
j































 ;
)
(
1
1
1
0
1
1
1
0
0
Para el conjunto de nodos x0, x1, x2, …, xn, estos polinomios son conocidos como funciones cardinales.
Utilizando estos polinomios en la ecuación de P(x) obtenemos la forma exacta del polinomio de
interpolación de Lagrange.

Pág. Nº 5
Error asociado al polinomio de interpolación de Lagrange
Teorema: Si x0, x1,   , xn; son puntos en el intervalo cerrado [a, b] y f tiene n+1 derivadas continuas en dicho
intervalo. Entonces, para cada x en [a, b] y un c(x) en (a, b) existe
f(x) = P(x) +
 
 
    
n
n
x
x
x
x
x
x
n
x
f








1
0
1
1
)
(
donde P es el polinomio de interpolación de Lagrange de f y
Rn(x) =
 
 
    
n
n
x
x
x
x
x
x
n
x
c
f








1
0
1
1
))
(
(
; con c(x) un punto en el intervalo [a, b],
es la fórmula del residuo o error; esta fórmula es un resultado teórico muy importante ya que los polinomios de
Lagrange se usan extensamente para deducir métodos de diferenciación e integración.
Observaciones:
1. La fórmula del error del polinomio de Taylor toma en cuenta solamente un punto (“a” o “x0”): Rn(x) =
 
 
 
0
1
!
1
))
(
(
x
x
n
x
c
f n



, c(x) un punto entre x0 y x, mientras que la del polinomio de Lagrange utiliza la
información de todos los (n +1) puntos: xo, x1, ..., xn.
2. Una desventaja de la fórmula del residuo asociado al polinomio de Lagrange es que necesita, al igual que el
de Taylor, conocer la derivada de orden n+1 de la función o una cota de ella dentro del intervalo [a, b].
Ejemplo 1
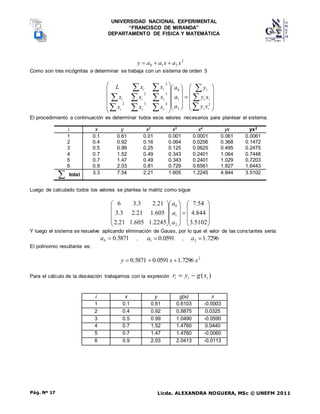
Calcular el polinomio de Lagrange usando los siguientes datos:
Solución. Tenemos que:
)
(
)
(
)
(
)
(
)
( 3
3
2
1
1
0
0 x
l
y
x
l
y
x
l
y
x
l
y
x
f 



)
(
3
)
(
2
)
(
)
(
2
)
( 3
2
1
0 x
l
x
l
x
l
x
l
x
f 




donde:
48
)
7
)(
5
)(
3
(
)
6
)(
4
)(
2
(
)
7
)(
5
)(
3
(
)
(
0












x
x
x
x
x
x
x
l
16
)
7
)(
5
)(
1
(
)
4
)(
2
)(
2
(
)
7
)(
5
)(
1
(
)
(
1










x
x
x
x
x
x
x
l
16
)
7
)(
3
)(
1
(
)
2
)(
2
)(
4
(
)
7
)(
3
)(
1
(
)
(
2










x
x
x
x
x
x
x
l
48
)
5
)(
3
)(
1
(
)
2
)(
4
)(
6
(
)
5
)(
3
)(
1
(
)
(
3








x
x
x
x
x
x
x
l

Pág. Nº 6
Sustituyendo arriba, el polinomio de Lagrange queda definido como sigue:





 








 








 








 



16
)
5
)(
3
)(
1
(
8
)
7
)(
3
)(
1
(
16
)
7
)(
5
)(
1
(
24
)
7
)(
5
)(
3
(
)
(
x
x
x
x
x
x
x
x
x
x
x
x
x
f
Ejemplo 2.
Calcular el polinomio de Lagrange usando los siguientes datos:
Solución. Tenemos que:
)
(
)
(
)
(
)
(
)
( 3
3
2
1
1
0
0 x
l
y
x
l
y
x
l
y
x
l
y
x
f 



)
(
2
)
(
3
)
(
)
(
)
( 3
2
1
0 x
l
x
l
x
l
x
l
x
f 



donde:
48
)
4
)(
2
(
)
6
)(
4
)(
2
(
)
4
)(
2
)(
0
(
)
(
0











x
x
x
x
x
x
x
l
16
)
4
)(
2
)(
2
(
)
4
)(
2
)(
2
(
)
4
)(
2
)(
2
(
)
(
1










x
x
x
x
x
x
x
l
16
)
4
)(
2
(
)
2
)(
2
)(
4
(
)
4
)(
0
)(
2
(
)
(
2









x
x
x
x
x
x
x
l
48
)
2
)(
2
(
)
2
)(
4
)(
6
(
)
2
)(
0
)(
2
(
)
(
3







x
x
x
x
x
x
x
l
Sustituyendo arriba, el polinomio de Lagrange queda como sigue:





 

















 













24
)
2
)(
2
(
16
)
4
)(
2
(
3
16
)
4
)(
2
)(
2
(
48
)
4
)(
2
(
)
(
x
x
x
x
x
x
x
x
x
x
x
x
x
f
Ejemplo 3.:
Determine el polinomio cuadrático que pasa por los siguientes puntos: (-2, 4), (0, 2) y (2, 8).
Solución:
L0 = ;
8
)
2
(
)
2
2
)(
0
2
(
)
2
)(
0
( 






 x
x
x
x
L1 =
4
)
2
)(
2
(
)
2
0
))(
2
(
0
(
)
2
))(
2
(
( 








 x
x
x
x

Pág. Nº 7
L2 =
8
)
2
(
)
0
2
))(
2
(
2
(
)
0
))(
2
(
( 






 x
x
x
x
Luego: P(x) = L0y0 + L1y1 + L2y2 = 2
8
8
)
2
(
2
4
)
2
(
2
(
4
8
)
2
( 2









x
x
x
x
x
x
x
x
Ejemplo 4.:
Dado el Ln(2)
a) Use una interpolación del polinomio de primer y segundo orden para evaluar ln2 con los
siguientes puntos x0 = 1, x1 = 4 y x2 = 6.
b) Estime el error en cada caso.
c) Compare con el valor verdadero.
Solución: (a)
ln(4) = 1.3863; ln(6) = 1.7918 De acuerdo a la fórmula se tiene:
P1(2) = 4621
.
0
3863
.
1
1
4
1
2
0
4
1
4
2






; ln(2)-P1(2)= 0.6932-0.4621 = 0.2311
P2(2) = 56584
.
0
7918
.
1
)
4
6
)(
1
6
(
)
4
2
)(
1
2
(
3863
.
1
)
6
4
)(
1
4
(
)
6
2
)(
1
2
(
0
)
6
1
)(
4
1
(
)
6
2
)(
4
2
(















ln(2) – P2(2)  = 0.69315 – 0.56584 = 0.12731, con P2 se obtiene una mejor aproximación.
Solución (b)
Para f(x) =ln(x),f(x) = -x-2,f(3)(x)=2x-3; E1(x) = )
4
)(
1
(
2
)
(
"

 x
x
z
f
E1(2)=   
4
2
1
2
2
1
2


z

como 1<x<6 entonces 1/6<1/x<1 por lo tanto 1/z2 < 1, luego E1(2) <2/2 = 1.
 E2(2) = 
 
   
6
2
4
2
1
2
6
)
(
3



z
f
< 2/3, ya que 1/z3<1. 
(b) Interpolación del Polinomio de Newton.
Este es otro método a desarrollar para obtener aproximaciones polinómicas de funciones, el cual
presenta las siguientes ventajas con respecto al método de Lagrange:
 La cantidad de cálculos necesaria para interpolar es menor.
 La interpolación para otro valor de x no necesita de cantidad de cálculos adicionales, ya que se pueden
utilizar partes de aplicaciones previas.
 Cuando el número de datos tiene que crecer o decrecer, se pueden utilizar los resultados de los
cálculos previos.
 La evaluación del error es más fácil.
De la definición de derivada en un punto x = z se puede encontrar una aproximación para la pendiente
que pasa por los puntos (x, y(x)), (z, y(z)):

Pág. Nº 8
f’(z) =
z
x
z
f
x
f
lím
z
x 


)
(
)
(
 f’(z)
z
x
z
y
x
y
z
x
z
f
x
f






)
(
)
(
)
(
)
(
= f[z, x] con esta notación indicaremos la
Primera Diferencia Dividida o diferencia dividida de primer orden(DD1).
Otra manera de relacionar la derivada y la diferencia dividida es mediante el teorema del valor medio:
Teorema de Valor Medio: Sea f una función definida y continua en el intervalo [a, b] y diferenciable
en (a, b). Entonces existe al menos un punto c en el abierto (a, b) tal que f’(c) =
a
b
a
f
b
f

 )
(
)
(
,b  a.
De esta manera, si x0 , x están en [a, b] en el que f es diferenciable se cumple:
f[x, x0] =
0
0 )
(
)
(
x
x
x
f
x
f


= f’(c), para algún c en (x0, x).
Deducción del polinomio de interpolación de Lagrange.
Sea Pn el n-ésimo polinomio de Lagrange que coincide con la función f en los n +1 puntos: x0, x1,   
xn. Obtendremos las diferencias divididas de f respecto a los n +1 puntos dados con f(x0) = y0, f(x1) = y1,    ,
f(xn) = yn; para expresar Pn(x) de la siguiente forma:
(*) Pn(x) = b0 + b1(x-x0) + b2(x-x0(x-x1 +    +bn(x-x0)(x-x1)    (x-xn-1), para constantes apropiadas: b0, b1,   ,
bn.
Para n = 0  b0 = P0(x0) = y0
n = 1  f(x1) = P1(x1) = b0 + b1(x1 – x0)  b1 = [f(x1) – f(x0) ]/ (x1 – x0) = DD1 (diferencias divididas de
orden uno)
Luego P1(x) = f(x0) + DD1 (x-x0) = f[x0] + f[x1, x0](x- x0).
f(xi) = f[xi] esta se denomina diferencia dividida de orden cero.
Con n = 2 se puede determinar b2 ya que se conocen b0 y b1: b2 = {f[x2, x1] – f[x1, x0]}/(x2 – x1)= DD2
observe que en el donominador va la diferencia de los puntos extremos: x2 y x0.
Luego P2(x) = f[x0] + f[x1, x0](x - x0) + f[x2, x1, x0](x-x0)(x –x1), y así sucesivamente se obtiene:
Pn(x) = f[x0] + f[x1, x0](x - x0) + f[x2, x1, x0](x-x0)(x –x1) +    + f[xn, xn-1,    , x1, x0](x-x0)(x –x1)    (x – xn-1).
FÓRMULA DE INTERPOLACIÓN DE DIFERENCIAS DIVIDIDAS DE NEWTON
ORDEN NOTACIÓN DEFINICIÓN O EXPRESIÓN
0 f[x0] = y0 f(x0)
1 f[x1, x0]
0
1
0
1 )
(
)
(
x
x
x
f
x
f


2 f[x2, x1, x0]    
0
2
0
1
1
2 ,
,
x
x
x
x
f
x
x
f


3 f[x3, x2, x1, x0]    
0
3
0
1
2
1
2
3 ,
,
,
,
x
x
x
x
x
f
x
x
x
f


- - - - - - - -
- - - - - - - -
n f[xn , xn-1,   , x1, x0]    
0
0
1
1
1 ,
,
,
,
,
x
x
x
x
f
x
x
x
f
n
n
n
n







 


Pág. Nº 9
Por ejemplo, para un polinomio de orden cuatro se tiene:
P4(x) = f[x0] + f[x1, x0](x - x0) + f[x2, x1, x0](x-x0)(x –x1) + f[x3, x2, x1, x0](x-x0)(x-x1)(x-x2)
+ f[x4 ,x3, x2, x1, x0](x-x0)(x-x1)(x-x2)(x-x3).
¿Cómo calcular las diferencias divididas?.
METODO DE LAS DIFERENCIAS DIVIDIDAS DE NEWTON
xi DD0 DD1 DD2 DD3
xo f(xo)
0
1
0
1 )
(
)
(
x
x
x
f
x
f

 =fx1,xo
x1 f(x1)    
0
2
0
1
1
2 ,
,
x
x
x
x
f
x
x
f

 =fx2, x1, xo
 
 
1
2
1
2
1
2
,
)
(
x
x
f
x
x
x
f
x
f


    
 
0
1
2
3
0
3
0
1
2
1
2
3
,
,
,
,
,
,
,
x
x
x
x
f
x
x
x
x
x
f
x
x
x
f



x2 f(x2)
     
1
2
3
1
3
1
2
2
3
,
,
,
,
x
x
x
f
x
x
x
x
f
x
x
f



   
 
2
3
2
3
2
3
, x
x
f
x
x
x
f
x
f


      
1
2
3
4
1
4
1
2
3
2
3
4
,
,
,
,
,
,
,
x
x
x
x
f
x
x
x
x
x
f
x
x
x
f



x3 f(x3)      
2
3
4
2
4
2
3
3
4
,
,
,
,
x
x
x
f
x
x
x
x
f
x
x
f



   
 
3
4
3
4
3
4
, x
x
f
x
x
x
f
x
f



x4 f(x4)
DD4 = f[x4, x3, x2, x1, x0] =
   
0
4
0
1
2
3
1
2
3
4 ,
,
,
,
,
,
x
x
x
x
x
x
f
x
x
x
x
f


.
El resto asociado a este polinomio:
Rn(x)  f 
o
n
n x
x
x
x
x ,
,.....,
,
, 1
1
 (x – xo)(x – x1)(x – x2)      (x – xn-1)(x – xn).
Siendo x un valor adicional para poder estimar el error.
Ejemplo 1. Calcular la tabla de diferencias divididas con los siguientes datos :
Y utilizar la información de dicha tabla, para construir el polinomio de interpolación de Newton.
Solución.
Procedemos como sigue:

Pág. Nº 10
Por lo tanto el polinomio de interpolación de Newton es :
)
2
)(
1
)(
2
(
3
.
0
)
1
)(
2
(
25
.
0
)
2
(
2
4
)
( 








 x
x
x
x
x
x
x
f
Ejemplo 2. Calcular la tabla de diferencias divididas con los siguientes datos :
Y usar la información en la tabla, para construir el polinomio de interpolación de Newton.
Solución. Procedemos como sigue:
Por lo tanto el polinomio de interpolación de Newton nos queda :
)
)(
2
)(
3
(
20238
.
0
)
2
)(
3
(
66667
.
1
)
3
(
3
5
)
( x
x
x
x
x
x
x
f 








Ejemplo3.: dada la siguiente tabla de valores:
i xi yi
0 0.1 0.99750
1 0.2 0.99002
2 0.4 0.96040
3 0.7 0.88120
4 1.0 0.76520
5 1.2 0.67113
6 1.3 0.62009
a) Elaborar una tabla de diferencia divididas
b) Escriba la fórmula de interpolación de Newton ajustada a la tabla de diferencias divididas.

Pág. Nº 11
c) Evalúe el polinomio resultante en x = 0.3
d) Estime el error en la interpolación.
Solución:
a) En primer término elaboramos la tabla de diferencias divididas:
i xi DDO DD1 DD2 DD3 DD4 DD5 DD6
0 0.1 0.99750
-0.07480
1 0.2 0.99002 -0.24433
-0.14810 0.02088
2 0.4 0.96040 -0.23180 0.01478
-0.26400 0.03418 -0.00236
3 0.7 0.88120 -0.20445 0.01218 0.00122
-0.38667 0.04636 -0.00090
4 1.0 0.76520 -0.16736 0.01119 0.00600
-0.47035 0.05643 -0.00030
5 1.2 0.67113 -0.13350 0.01122
-0.51040 0.05194
6 1.3 0.62009 -0.16986
-0.35753
0.3 0.97762
b) la formula de interpolación ajustada a los datos sería:
)
2
.
1
)(
1
)(
7
.
0
)(
4
.
0
)(
2
.
0
)(
1
.
0
(
00122
.
0
)
1
)(
7
.
0
)(
4
.
0
)(
2
.
0
)(
1
.
0
(
00236
.
0
)
7
.
0
)(
4
.
0
)(
2
.
0
)(
1
.
0
(
01478
.
0
)
4
.
0
)(
2
.
0
)(
1
.
0
(
02088
.
0
)
2
.
0
)(
1
.
0
(
24433
.
0
)
1
.
0
(
07480
.
0
99750
.
0
)
(
6




























x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
P
c) 97762
.
0
)
3
.
0
(
6 
P
d) Para estimar la cota del error se debe aplicar la siguiente ecuación:
R6(x)  f 
o
x
x
x
x
x
x
x
x ,
,
,
,
,
,
, 1
2
3
4
5
6 (x – xo)(x – x1)(x – x2) (x – x4)(x – x5)(x – x6).
La diferencia dividida de la ecuación se obtiene calculando la diferencia dividida que involucra el punto x = 0.3,
ubicando éste al final de la tabla y recalculando todas las diferencias nuevamente hasta llegar a la deseada.
R6(0.3)  0.0239(0.3 – 0.1)(0.3 – 0.2)(0.3 – 0.4) (0.3 – 0.7)(0.3 – 1.0)(0.3 – 1.2) = 1.205x10-5
EJERCICIOS PORPUESTOS
1.- Escriba una fórmula de interpolación lineal que aproxime sen(x) en el intervalo 0 x  /4 utilizando los
valores en x = 0 y x = /4. grafique el error para determinar el error máximo de la interpolación y en qué x
ocurre.
2.- Use los siguientes valores y la aritmética de redondeo a 4 cifras significativas para construir una
aproximación de f(1,09) utilizando polinomios de Lagrange. La función que va a ser aproximada es f(x) =
log10(tanx). Conociendo lo anterior, calcule una cota del error en la aproximación.
X0 = 1.00 X1 = 1.05 X2 = 1.10 X3 = 1.15
3 a) Escriba la fórmula de interpolación de Lagrange a través de los siguientes datos:
0.0239

Pág. Nº 12
x 0 0,4 0,8 1,2
f(x) 1,0 1,491 2,225 3,320
b) Conociendo fiv (0,6) = 1,822 estime el error en x = 0,2, 0,6 y 1,0 utilizando la fórmula del error en la
interpolación de Lagrange con c igual al punto medio.
a) Dado el hecho de que la tabla de datos se obtuvo de f(x) = ex, evalúe el error de la fórmula de
interpolación en x = 0,2, 0,6 y 1,0, usando las fórmulas de error absoluto y relativo.
4.- Para los datos:
x -1 0 1 2
y 1/3 1 3 9
Encuentre: a.) El polinomio de interpolación de Lagrange
b.) El polinomio de Interpolación de Newton
5.- Para los datos:
x 0 ½ 1 3/2
y 1 2 1 0
6.- Para los datos:
x -1 -0,75 -0,25 0,25 0,75 1
y 0 -0,7 -0,7 0,7 0,7 0
7- Con una función f la fórmula de las diferencias divididas interpolantes de Newton da el polinomio interpolante
P3(x) = 1 + 4x + 4x(x – 0.25) +
3
16
x(x – 0.25)(x – 0.5)
En los nodos x0 = 0, x1 = 0.25, x2 = 0.5 y x3 = 0.75. Obtenga f(0.75)
9.- Haga la tabla de difrencias divididas a partir de la siguiente tabla de valores:
i 1 2 3 4 5 6
x 0.5 1 1.5 2 2.5 3
y 1.143 1 0.828 0.667 0.533 0.428
por medio de las fórmulas de Newton, escriba los polinomios de Interpolación ajustados a:
a) i = 1,2,3
b) i = 4,5,6
c) i = 2,3,4,5
10.- Dada la tabla.
i 0 1 2 3
xi 1 1.35 1.70 1.90
f(xi) 0 0.30010 0.53063 0.64185
Construya una tabla de diferencias divididas para aproximar f(x) en x = 1.5. utilice un polinomio de Newton de
segundo grado.

Pág. Nº 13
11.- Cierta función discreta relaciona lasvariables “x” y “y” a través de la tabla:
x 0 1 2 2.5 3 3.5 4
y 2.50 1.15 0.50 1.20 1.50 1.125 0
a. Calcule el valor de y para un x = 1.125
b. Calcule el valor de x que corresponda a un y = 1.089
(Aplique para ambos casos polinomios de Newton y Polinomios de Lagrange).
Trazadores cúbico “Spline”
El objetivo de los spline es obtener un polinomio de tercer grado para cada intervalo entre los nodos, con la
finalidad de minimizar los errores de redondeo que pudieran aparecer al utilizar cualquiera de los métodos de
interpolación ya estudiados.
De estas nuevas funciones generadas se debe cumplir lo siguiente:
1.- Los valores de la función deben ser iguales en los nodos interiores.
2.- la primera y última función deben pasar a través de los puntos extremos.
3.- Las primeras y segundas derivadas en los nodos interiores deben ser iguales.
4.- Las segundas derivadas en los nodos extremos son cero.
Buscamos una función que interpole n puntos datos dados (xi, yi). Suponiéndose que x1 < x2 < ...< xn y sean x1 =
a y xn = b. Entonces se quiere construir una nueva función la cual denotaremos como S(x) tal que sobre [a,b],
se cumpla que S(xi)=yi.
Se quiere que sobre [a,b], S(x) sea una función suave por lo tanto S´(x) y S´´(x) deben ser continuas. Decir que
S(x) sea suave sobre [a,b] implica que la curvatura sea pequeña, eso es equivalente a decir que el valor de:
  dx
x
S
b
a
2
)
´´(
 debe ser pequeño.
La solución a lo planteado viene dada mediante una función interpolante que cumpla con dos condiciones:
 La función S(x) es un polinomio cúbico sobre cada subintervalo [xi ,xi+1], i = 1,2,3,...,n –1
 S´´(x1)= S´´(xn) = 0
Una función que cumpla con estas condiciones nos lleva a lo que se denomina segmentaria cúbica natural
(Spline natural).
Para construir los Spline en el subintervalo [xi ,xi+1] trabajaremos en base a la siguiente fórmula:
   
 
i
i
i
i
i M
w
w
M
w
w
h
y
w
y
w
x
S 






 

3
1
3
2
1
)
(
de donde :
hi es el tamaño del subintervalo donde se va a construir la función cúbica y se obtiene mediante la siguiente
expresión: hi = xi+1 – xi.
i
i
h
x
x
w

 es el único parámetro que no es constante. w
w 
1 es el complemento. Las constantes M son
parámetros que se pueden determinar mediante la siguiente ecuación:
  1
1
1
1
1 2 



 





 i
i
i
i
i
i
i
i
i M
h
M
h
h
M
h (*)

Pág. Nº 14
siendo
i
i
i
i
h
y
y 1



Con (*) se genera un sistema de n – 2 ecuaciones con n incógnitas que junto con Mo = Mn= 0 determinan un
Spline cúbico natural de manera única.
Observación: De la definición del polinomio cúbico se tiene:
Uno de las dos siguientes condiciones de frontera se satisface:
(i) S’’(x1) = S’’(xn) = 0, en este caso la Spline cúbica se denomina Natural
(esto es equivalente a decir que Mo = Mn= 0)
(ii) Si f es derivable en los extremos tal que S’(x1) = f’(x1) y S’(xn) = f’(xn), se dice entonces
que f tiene un adaptador cúbico no natural o fijo.
Ejercicio resuelto 1.: Dados los puntos (1, 1), (2, 1/2), (3, 1/3), (4, 1/4) Determine la Spline cúbica natural para
este conjunto de puntos con hi = 1.
Solución: Como se pide que la Spline sea natural entonces Mo = M3 = 0.
Al ser cuatro puntos se tienen tres subintervalos y n = 4, por lo tanto para i = 1,2 se tiene:
   
 
i
i
i
i
i M
w
w
M
w
w
h
y
w
y
w
x
S 






 

3
1
3
2
1
)
(
trabajamos con i = 1 e i = 2 para generar un sistema de ecuaciones que nos permita determinar las M
faltantes.
2
1
1
1
2
/
1
0
0
1
0 






h
y
y
6
1
1
2
/
1
3
/
1
1
1
2
1 






h
y
y
12
1
1
3
/
1
4
/
1
2
2
3
2 






h
y
y
i = 1
  0
1
2
1
1
1
0
0
0 2 





 M
h
M
h
h
M
h
4M1 + M2 = 1/3 (**)
i = 2
  1
2
3
2
2
2
1
1
1 2 





 M
h
M
h
h
M
h
M1 + 4M2 = 1/12 (***)
Como se puede notar (**) y (***) forman un sistema de 2 ecuaciones con 2 incógnitas cuya solución es:
M1 = 1/12 M2 = 0
Los Spline para cada subintervalos serán:
1  x  2
   
 
1
3
2
3
2
1
1
2
)
( M
w
w
M
w
w
h
y
w
y
w
x
S 







)
1
(
1



 x
h
x
x
w
i
y x
x
w 



 2
)
1
(
1 y se sustituyen en la ecuación para obtener la función cúbica:
este proceso se repite para los otros spline de los demás subintervalos.
0
0

Pág. Nº 15
  12
/
1
)
1
(
)
1
(
)
2
(
)
1
(
2
/
1
)
( 3







 x
x
x
x
x
S
2  x  3
  12
/
1
)
3
(
)
3
(
)
3
(
2
/
1
)
2
(
3
/
1
)
( 3
x
x
x
x
x
S 







3  x  4
)
4
(
3
/
1
)
3
(
4
/
1
)
( x
x
x
S 



2.3.- Ajuste de Curvas por mínimos cuadrados:
Esta es una técnica de optimización matemática que, dada una serie de mediciones, intenta encontrar
una función que se aproxime a los datos (un mejor ajuste).
La idea es considerar una función con pocos parámetros libre y determinarlos de forma que la
desviación de la función con respecto a los datos sea mínima. Dicha minimización de la desviación de la función
se obtiene mediante el método de los mínimos cuadrados.
El método de los mínimos cuadrados se puede aplicar para ajustar un polinomio de cualquier orden a
los datos de una medición.
Sea
n
n x
a
x
a
x
a
a
x
g 



 ...
)
( 2
2
1
0
La desviación de la curva de los puntos dados es:
)
( i
i
i x
g
y
r 
 i = 0, 1, 2,…,L
Siendo L el número de puntos dados.
El cuadrado total de las desviaciones es:
 



L
i
i
r
R
1
2
   

 









L
i
n
i
n
i
i
i
L
i
i
i x
a
x
a
x
a
a
y
x
g
y
R
1
2
2
2
1
0
1
2
...
)
(
Como se desconoce el valor de las constantes del polinomio, se deben determinar de forma que se
minimice el valor de R. El mínimo de R se obtiene si las derivadas parciales con respecto a los coeficientes del
polinomio se anulan.
0



n
a
R
 











 L
i
n
i
n
i
i
i x
a
x
a
x
a
a
y
a
R
1
2
2
1
0
0
0
)
1
(
...
2

Pág. Nº 16
 











 L
i
i
n
i
n
i
i
i x
x
a
x
a
x
a
a
y
a
R
1
2
2
1
0
1
0
)
(
...
2

 











 L
i
n
i
n
i
n
i
i
i
n
x
x
a
x
a
x
a
a
y
a
R
1
2
2
1
0 0
)
(
...
2
Dividiendo todo entre -2 y despejando se obtiene:
 


  








L
i
L
i
i
n
i
n
L
i
i
L
i
i
L
i
y
x
a
x
a
x
a
a
1 1
1
2
2
1
1
1
0 ...
 


  









L
i
L
i
i
i
n
i
n
L
i
i
L
i
i
L
i
i x
y
x
a
x
a
x
a
x
a
1 1
1
1
3
2
1
2
1
1
0 ...

 


  










L
i
L
i
n
i
i
n
i
n
L
i
n
i
L
i
n
i
L
i
n
i x
y
x
a
x
a
x
a
x
a
1 1
2
1
2
2
1
1
1
1
0 ...
Expresando este sistema en forma matricial se tiene:












































































n
i
i
i
i
i
i
i
n
n
i
n
i
n
i
n
i
n
i
i
i
i
n
i
i
i
i
n
i
i
i
x
y
x
y
x
y
y
a
a
a
a
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
L








2
2
1
0
2
2
1
2
4
3
2
1
3
2
2
...
...
...
Las constantes ai i = 0,…,n se determinan aplicando el método de eliminación de Gauss.
Ejercicio resuelto 2.: Ajuste un polinomio cuadrático a los datos de la tabla mediante los mínimos cuadrados y
calcule su desviación.
i x y
1 0.1 0.61
2 0.4 0.92
3 0.5 0.99
4 0.7 1.52
5 0.7 1.47
6 0.9 2.03
Solución: planteamos primeramente el polinomio del orden especificado en el planteamiento y luego generamos
el sistema adaptado al número de incógnitas presentes.

Pág. Nº 17
2
2
1
0 x
a
x
a
a
y 


Como son tres incógnitas a determinar se trabaja con un sistema de orden 3












































2
2
1
0
4
3
2
3
2
2
i
i
i
i
i
i
i
i
i
i
i
i
i
x
y
x
y
y
a
a
a
x
x
x
x
x
x
x
x
L
El procedimiento a continuación es determinar todos esos valores necesarios para plantear el sistema.
Luego de calculado todos los valores se plantea la matriz como sigue































5102
.
3
844
.
4
54
.
7
2245
.
1
605
.
1
21
.
2
605
.
1
21
.
2
3
.
3
21
.
2
3
.
3
6
2
1
0
a
a
a
Y luego el sistema se resuelve aplicando eliminación de Gauss, por lo que el valor de las constantes sería:
5871
.
0
0 
a , 0591
.
0
1 
a , 7296
.
1
2 
a
El polinomio resultante es:
2
7296
.
1
0591
.
0
5871
.
0 x
x
y 


Para el cálculo de la desviación trabajamos con la expresión )
( i
i
i x
g
y
r 

i x y g(xi) ri
1 0.1 0.61 0.6103 -0.0003
2 0.4 0.92 0.8875 0.0325
3 0.5 0.99 1.0490 -0.0590
4 0.7 1.52 1.4760 0.0440
5 0.7 1.47 1.4760 -0.0060
6 0.9 2.03 2.0413 -0.0113
i x y x2 x3 x4 yx yx2
1 0.1 0.61 0.01 0.001 0.0001 0.061 0.0061
2 0.4 0.92 0.16 0.064 0.0256 0.368 0.1472
3 0.5 0.99 0.25 0.125 0.0625 0.495 0.2475
4 0.7 1.52 0.49 0.343 0.2401 1.064 0.7448
5 0.7 1.47 0.49 0.343 0.2401 1.029 0.7203
6 0.9 2.03 0.81 0.729 0.6561 1.827 1.6443
 total 3.3 7.54 2.21 1.605 1.2245 4.844 3.5102

Pág. Nº 18
EJERCICIOS PROPUESTOS
1.- Para los datos:
X -1 0 1 2
Y 1/3 1 3 9
c.) El Spline cúbico natural.
d.) Ajuste de curvas por mínimos cuadrados mediante un polinomio lineal, cuadrático y cúbico.
2.- Para los datos:
X 0 ½ 1 3/2
Y 1 2 1 0
d.) Ajuste de curvas por mínimos cuadrados mediante un polinomio lineal, cuadrático y cúbico.
3.- Para los datos:
X -1 -0,75 -0,25 0,25 0,75 1
Y 0 -0,7 -0,7 0,7 0,7 0
d.) El Spline cúbico no natural.
e.) Ajuste de curvas por mínimos cuadrados mediante un polinomio lineal, cuadrático y cúbico.
Compare los valores interpolados en x = -0,5 y x = 0,5 con los valores de f(x) = sen(x)
4.- Construya un Spline cúbico no natural para aproximar f(x) = sen(ex – 2) utilizando los valores dados por f(x)
en x = 0.7 ; 0.8 ; 0.9 ; 1.0, para aproximar f(0.85). Use las derivadas del Spline para aproximar f ´(0.85),
compare las aproximaciones con los valores reales.
5.- Con una función f la fórmula de las diferencias divididas interpolantes de Newton da el polinomio
interpolante
P3(x) = 1 + 4x + 4x(x – 0.25) +
3
16
x(x – 0.25)(x – 0.5)
En los nodos x0 = 0, x1 = 0.25, x2 = 0.5 y x3 = 0.75. Obtenga f(0.75)
6.- Haga la tabla de diferencias divididas a partir de la siguiente tabla de valores:
i 1 2 3 4 5 6
x 0,5 1 1,5 2 2,5 3
y 1,143 1 0,828 0,667 0,533 0,428
por medio de las fórmulas de Newton, escriba los polinomios de Interpolación ajustados a:

Pág. Nº 19
d) i = 1,2,3
e) i = 4,5,6
f) i = 2,3,4,5
7.- Dada la tabla:
I 0 1 2 3
xi 1 1.35 1.70 1.90
f(xi) 0 0.30010 0.53063 0.64185
Construya una tabla de diferencias divididas para aproximar f(x) en x = 1.5. utilice un polinomio de Newton de
segundo grado.
8.- Cierta función discreta relaciona lasvariables “x” y “y” a través de la tabla:
x 0 1 2 2.5 3 3.5 4
y 2.50 1.15 0.50 1.20 1.50 1.125 0
c. Calcule el valor de y para un x = 1.125
d. Calcule el valor de x que corresponda a un y = 1.089
(Aplique para ambos casos polinomios de Newton y Polinomios de Lagrange).
9.-
a) a.- Construya un Spline cúbico no natural para aproximar f(x) = ln(x4+ 3) utilizando los valores para f(x)
dados en x = 0, 0.3, 0.5, 0.75 y 1.
b) b.- Integre el spline sobre 0,1 y compare su resultado con el valor exacto.
c) c.- Use las derivadas del spline para aproximar f´(0,5) y f´´(0,5) compare con los valores verdaderos.
10.- Durante un período de tres horas, la distancia desde la línea de la marea a una marca fija es medida:
t 0 1 2 3 Horas
d 20 10 8 15 Metros
Estime mediante Polinomios de Lagrange y de Newton con 4 decimales la distancia mínima de la línea de
marca durante este período.

Aproximacion_Interpolacion.doc

Más contenido relacionado

Similar a Aproximacion_Interpolacion.doc

Más de SistemadeEstudiosMed

Último

Aproximacion_Interpolacion.doc