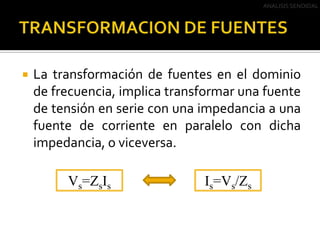
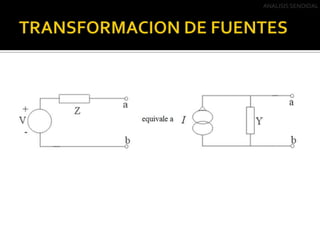
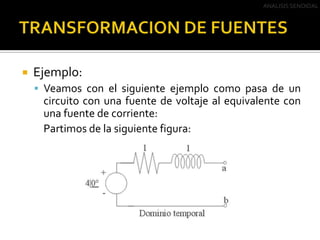
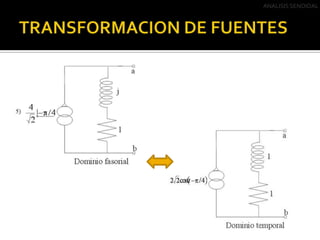
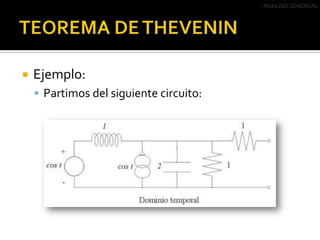
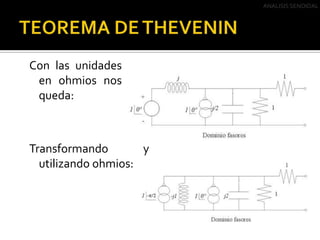
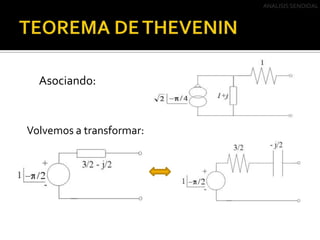
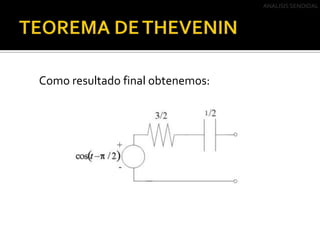
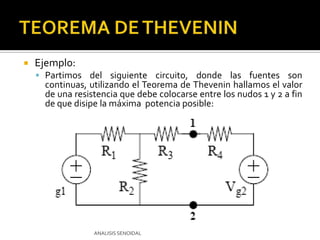
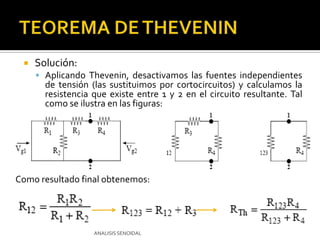
Este documento describe el análisis de circuitos eléctricos de corriente alterna mediante el uso de fasores. Explica que el análisis en el dominio de la frecuencia es más fácil que en el dominio del tiempo. También cubre las transformaciones de fuentes y el Teorema de Thevenin, incluyendo ejemplos de cómo aplicar estos conceptos para simplificar circuitos de corriente alterna.

1. ANALISIS MEDIANTE FASORESCIRCUITOS ELECTRICOS IUNIVERSIDAD FERMIN TORODecanato de Ingeniería SAIA - EXTENSION SAN FELIPE

2. ANALISIS SENOIDALEl análisis en el dominio de frecuencia de un circuito de ca por medio de fasores es mucho mas fácil que el análisis del circuito en el dominio del tiempo.El análisis de circuitos ca suele implicar tres pasos fundamentales:Transformar el circuito al dominio fasorial o de frecuencia.Resolver el problema aplicando técnicas de circuitos (análisis nodal, de malla, superposición, en otros).Transformar el fasor resultante al dominio del tiempo.ANALISIS SENOIDAL

3. Una transformación de fuentes es un procedimiento para sustituir una clase de fuente por otra, conservando las características de la fuente original. Las transformaciones se basan en el principio de equivalencia. Un circuito es equivalente cuando sus características en los terminales de referencia permanecen idénticos respecto al circuito original, de tal forma que tienen el mismo voltaje en circuito abierto y la misma corriente en corto circuito.ANALISIS SENOIDALTRANSFORMACION DE FUENTES

4. TRANSFORMACION DE FUENTESANALISIS SENOIDALLa transformación de fuentes en el dominio de frecuencia, implica transformar una fuente de tensión en serie con una impedancia a una fuente de corriente en paralelo con dicha impedancia, o viceversa.Vs=ZsIsIs=Vs/Zs

5. TRANSFORMACION DE FUENTESANALISIS SENOIDAL

6. TRANSFORMACION DE FUENTESANALISIS SENOIDALEjemplo:Veamos con el siguiente ejemplo como pasa de un circuito con una fuente de voltaje al equivalente con una fuente de corriente: Partimos de la siguiente figura:

7. TRANSFORMACION DE FUENTESANALISIS SENOIDAL

8. TRANSFORMACION DE FUENTESANALISIS SENOIDAL

9. TRANSFORMACION DE FUENTESANALISIS SENOIDAL

10. El Teorema de Thévenin establece que si una parte de un circuito eléctrico lineal está comprendida entre dos terminales A y B, esta parte en cuestión puede sustituirse por un circuito equivalente que esté constituido únicamente por un generador de tensión en serie con una impedancia, de forma que al conectar un elemento entre las dos terminales A y B, la tensión que cae en él y la intensidad que lo atraviesa son las mismas tanto en el circuito real como en el equivalente.ANALISIS SENOIDALTEOREMA DE THEVENIN

11. TEOREMA DE THEVENINANALISIS SENOIDALTodos los circuitos con fuentes y elementos de 2 terminales tienen equivalente de Thevenin. Los mecanismos son los mismos que se utilizan para las circuitos de corriente continua.Vth= voltaje en un circuito abierto en el par de nodos.Zth= impedancia vista en esos nodos.La fuente de tensión Thevenin, será ahora una fuente de tensión alterna.

12. TEOREMA DE THEVENINANALISIS SENOIDALEjemplo:Partimos del siguiente circuito:

13. TEOREMA DE THEVENINANALISIS SENOIDALCon las unidades en ohmios nos queda:Transformando y utilizandoohmios:

14. TEOREMA DE THEVENINANALISIS SENOIDALAsociando:Volvemos a transformar:

15. TEOREMA DE THEVENINANALISIS SENOIDALComo resultado final obtenemos:

16. ANALISIS SENOIDALEjemplo:

17. Partimos del siguiente circuito, donde las fuentes son continuas, utilizando el Teorema de Thevenin hallamos el valor de una resistencia que debe colocarse entre los nudos 1 y 2 a fin de que disipe la máxima potencia posible:TEOREMA DE THEVENIN