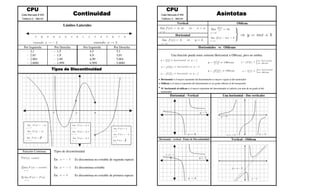
El documento describe diferentes tipos de discontinuidad y asintotas en funciones. Explica que una función puede tener una asintota horizontal u oblicua, pero no ambas. También describe cómo determinar si una función tiene una asintota horizontal, oblicua o ninguna, dependiendo de los exponentes en el numerador y denominador de la función. Además, explica los conceptos de continuidad y límites laterales.

1. - 2,1 - 1,5 4,5 5,1
- 2,01 - 1,9 4,9 5,01
- - 1,99 4,99
- 2,0001 -
• Horizontal si el mayor exponente del denominador es mayor o igual al del numerador
• Oblicua si el mayor exponente del denominador es un grado inferior al del numerador
•
Tipos de discontinuidad
En Es discontinua no evitable de segunda especie
2) En Es discontinua evitable
En Es discontinua no evitable de primera especie
Horizontal - Vertical
Horizontal - vertical - Punto de Discontinuidad
Una horizontal - Dos verticales
OblicuaVertical
Horizontal
Horizontales vs Oblicuas
Una función puede tener asíntota Horizontal u Oblicua, pero no ambas.
Ni horizontal, ni oblicua si el mayor exponente del denominador es inferior con más de un grado al del
numerador
Vertical - Oblicua
Límites Laterales
-7 -6 -5 -4 -3 2 3 4 75-2 -1 0 6 81
CPUCPUCPUCPU
AsíntotasAsíntotasAsíntotasAsíntotasCalle Mercado # 555
Teléfono 3 - 366191
3)
Función Continua
4.999
CPUCPUCPUCPU
Calle Mercado # 555
Teléfono 3 - 366191
ContinuidadContinuidadContinuidadContinuidad
Por Izquierda Por Derecha Por Izquierda
1)
Por Derecha
5,0001
Tipos de DiscontinuidadTipos de DiscontinuidadTipos de DiscontinuidadTipos de Discontinuidad
1.999
2.001 5.001
lim
x→à5à
F x( ) = à 2
lim
x→à5+
F x( ) = à 2
lim
x→à 5
F x( ) = à 2
cuando x → à 2 cuando x → 5
lim
x→à7à
F x( ) = à ∞
lim
x→à7+
F x( ) = ∞
lim
x→à7
F x( ) = ∃
lim
x→à1à
F x( ) = 2, 5
lim
x→à1+
F x( ) = 2, 5
lim
x→4à
F x( ) = 2
lim
x→4+
F x( ) = à 6
lim
x→4
F x( ) = ∃
lim
x→a
F x( ) = existe!
lim
x→a
F x( ) = F a( )
F a( ) existe!
x = à 7
x = à 1
x = 4
x = 3
y = 1
lim
x→a
f x( ) = æ ∞ ⇒ x = a
lim
x→∞
f x( ) = L ⇒ y = L
lim
x→∞
x
f(x)
= m
lim
x→∞
f(x) à mx = b
⇒ y = mx + b
y = cx+d
ax+b
⇒ horizontal en y = c
a
y = ax2+bx+c
nx+m
⇒ horizontal en y = 0
y = ax2+bx+c
nx2
+m
⇒ horizontal en y = a
n
y = cx+d
ax2
+b
⇒ Oblicua
y = ax2+bx+c
nx3
+m ⇒ Oblicua
y = ax2+bx+c
nx4
+m
⇒
no horizontal
no oblicua
ú
y = bx+c
nx3
+m
⇒
no horizontal
no oblicua
ú
lim
x→à1
F x( ) = 2, 5
y = 1
x = 3
x = à 1
y = 0
x = à 2 x = 3
x = 1
y = x à 2