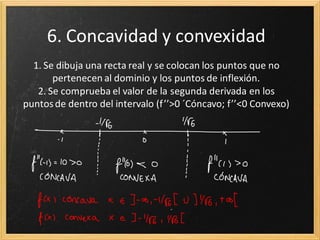
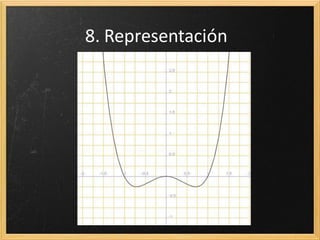
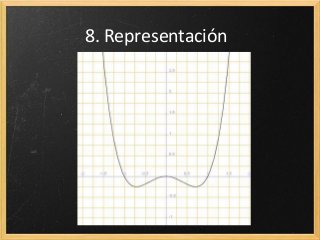
Este documento presenta los conceptos clave para representar funciones polinómicas, incluyendo: 1) dominio, 2) puntos de corte, 3) máximos y mínimos calculados a través de derivadas, 4) crecimiento y decrecimiento determinados por la derivada primera, 5) puntos de inflexión calculados con la derivada segunda, 6) concavidad y convexidad determinadas por la derivada segunda, y 7) asíntotas halladas a través de límites. El documento concluye explicando el orden para representar gráficamente una función polin

1. 7.1 REPRESENTACIÓN DE
FUNCIONES POLINÓMICAS
Matemáticas aplicadas a las
Ciencias Sociales II

2. ¿Qué vamos a ver hoy?
1.
2.
3.
4.
5.
6.
7.
Dominio
Puntos de corte
Máximos y mínimos
Crecimiento y decrecimiento
Puntos de inflexión
Concavidad y convexidad
Asíntotas

3. 1. Dominio

4. 1. Dominio
El dominio de una función son todos los valores de la x, que
sustituidos en la función no dan cosas «raras»

5. 1. Dominio
El dominio de una función son todos los valores de la x, que
sustituidos en la función no dan cosas «raras»

6. 2. Puntos de corte

7. 2. Puntos de corte
Para calcular los puntos de corte con el eje de las X,
igualamos la función a 0 y despejamos el valor de y (x, 0)

8. 2. Puntos de corte
Para calcular los puntos de corte con el eje de las X,
igualamos la función a 0 y despejamos el valor de y (x, 0)

9. 2. Puntos de corte
Para calcular los puntos de corte con el eje de las X,
igualamos la función a 0 y despejamos el valor de y (x, 0)
Para calcular los puntos de corte con el eje de las Y, hacemos
x=0 y obtenemos el valor correspondiente de y (0,y)

10. 2. Puntos de corte
Para calcular los puntos de corte con el eje de las X,
igualamos la función a 0 y despejamos el valor de y (x, 0)
Para calcular los puntos de corte con el eje de las Y, hacemos
x=0 y obtenemos el valor correspondiente de y (0,y)

11. 3. Máximos y mínimos

12. 3. Máximos y mínimos
Para obtener los posibles máximos y mínimos realizamos la
primera derivada de la función y la igualamos a cero.

13. 3. Máximos y mínimos
Para obtener los posibles máximos y mínimos realizamos la
primera derivada de la función y la igualamos a cero.

14. 3. Máximos y mínimos
Para obtener los posibles máximos y mínimos realizamos la
primera derivada de la función y la igualamos a cero.
Para saber sin son máximos o mínimos se sustituye en la
segunda derivada (f’’>0 mínimo; f’’<0 máximo)

15. 3. Máximos y mínimos
Para obtener los posibles máximos y mínimos realizamos la
primera derivada de la función y la igualamos a cero.
Para saber sin son máximos o mínimos se sustituye en la
segunda derivada (f’’>0 mínimo; f’’<0 máximo)

16. 4. Crecimiento y Decrecimiento

17. 4. Crecimiento y Decrecimiento
1. Se dibuja una recta real y se colocan los puntos que no
pertenecen al dominio, los máximos y los mínimos.
2. Se comprueba el valor de la primera derivada en los puntos
de dentro del intervalo (f’>0 Crece; f’<0 Decrece)

18. 4. Crecimiento y Decrecimiento
1. Se dibuja una recta real y se colocan los puntos que no
pertenecen al dominio, los máximos y los mínimos.
2. Se comprueba el valor de la primera derivada en los puntos
de dentro del intervalo (f’>0 Crece; f’<0 Decrece)

19. 5. Puntos de inflexión

20. 5. Puntos de inflexión
Para obtener los posibles puntos de inflexión realizamos la
segunda derivada de la función y la igualamos a cero.

21. 5. Puntos de inflexión
Para obtener los posibles puntos de inflexión realizamos la
segunda derivada de la función y la igualamos a cero.

22. 5. Puntos de inflexión
Para obtener los posibles puntos de inflexión realizamos la
segunda derivada de la función y la igualamos a cero.
Para saber sin son puntos que pasan de convexo a cóncavo o
de cóncavo a convexo se sustituye en la tercera derivada
(f’’’>0 CV-CX; f’’’<0 CX-CV)

23. 5. Puntos de inflexión
Para obtener los posibles puntos de inflexión realizamos la
segunda derivada de la función y la igualamos a cero.
Para saber sin son puntos que pasan de convexo a cóncavo o
de cóncavo a convexo se sustituye en la tercera derivada
(f’’’>0 CV-CX; f’’’<0 CX-CV)

24. 6. Concavidad y convexidad

25. 6. Concavidad y convexidad
1. Se dibuja una recta real y se colocan los puntos que no
pertenecen al dominio y los puntos de inflexión.
2. Se comprueba el valor de la segunda derivada en los
puntos de dentro del intervalo (f’’>0 ´Cóncavo; f’’<0 Convexo)

26. 6. Concavidad y convexidad
1. Se dibuja una recta real y se colocan los puntos que no
pertenecen al dominio y los puntos de inflexión.
2. Se comprueba el valor de la segunda derivada en los
puntos de dentro del intervalo (f’’>0 ´Cóncavo; f’’<0 Convexo)

27. 7. Asíntotas
Para las asíntotas verticales se realiza el límite en los puntos
que no pertenecen al dominio, buscando los límites infinitos y
obtener rectas del tipo x=a
Para las asíntotas horizontales se realizan los límites en más y
menos infinito, para obtener rectas del tipo y=b
Se calcula la pendiente y ordenada en el origen, para obtener
rectas y=mx + n

28. 7. Asíntotas
Para las asíntotas verticales se realiza el límite en los puntos
que no pertenecen al dominio, buscando los límites infinitos y
obtener rectas del tipo x=a
Para las asíntotas horizontales se realizan los límites en más y
menos infinito, para obtener rectas del tipo y=b
Se calcula la pendiente y ordenada en el origen, para obtener
rectas y=mx + n

29. 8. Representación
Para representar se sigue el siguiente orden:
1. Dibujar las asíntotas y estudiar los límites infinitos y en el
infinito.
2. Colocar los puntos de corte.
3. Colocar los máximos y mínimos.
4. Dibujar la función teniendo en cuenta el crecimiento y
decrecimiento, la concavidad y convexidad.

30. 8. Representación