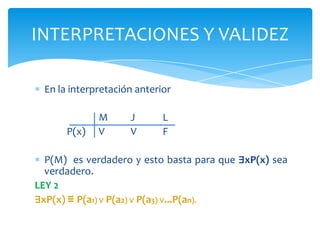
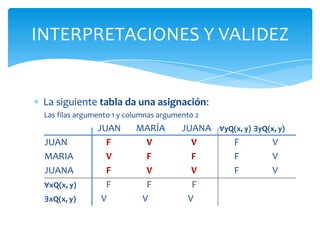
1) El documento habla sobre la interpretación de sentencias lógicas y la corrección de argumentos lógicos. 2) Una interpretación debe contener información suficiente para determinar si una frase es verdadera o falsa, como el universo de discurso y las asignaciones de predicados. 3) Para que un argumento sea válido, debe ser verdadero bajo todas las interpretaciones.