El documento habla sobre sistemas basados en lógica formal. Explica conceptos como inferencia, razonamiento, reglas de inferencia lógica, métodos de razonamiento lógico, definición de predicados, características de los predicados, ejemplos de predicados, axiomas, patrones, y procesos como la unificación y normalización de expresiones.

1. SISTEMAS BASADOS EN LÓGICA FORMAL

2. Inferencia y Razonamiento Inferir es sacar una consecuencia categórica, indiscutible, a partir de hechos conocidos o asumidos como verdaderos. Realizar inferencias significa derivar nuevos hechos inobjetables , a partir de un conjunto de hechos dados como verdaderos. Razonar es discurrir, dando razones, para llegar a conclusiones o probar algo. El proceso de razonamiento permite llegar a conclusiones que pueden o no ser correctas , a partir de un conjunto de hechos conocidos como verdaderos.

3. Reglas de Inferencia Lógica Modus Ponens Si p y ( p  q ) son verdaderas, entonces q tiene que ser verdadera. Modus Tolens Si ( p  q ) es verdadera y q es falsa, entonces p tiene que ser falsa. Resolución Si ( p  q ) es verdadera y (~q  r ) es verdadera, entonces ( p  r ) tiene que ser verdadera.

4. Métodos de Razonamiento Lógico Deductivo : Sus conclusiones son siempre correctas. Forma monotónica de realizar inferencias. Para todo p , q , r ; si p mayor que q y q mayor que r , entonces p mayor que r . Abductivo : Sus conclusiones pueden o no ser correctas. Es un método para generar explicaciones. Si ( p  q ) es verdadera y q es verdadera, entonces p podría ser verdadera. Inductivo : Sus conclusiones pueden o no ser correctas. Es la base de la investigación científica. Si P(a), P(b), ... P(n) son verdaderos, entonces se puede concluir que para todo x , P(x) puede ser verdadero.

5. Definición de Predicado Una sentencia expresa relaciones entre entre objetos , así como también cualidades y atributos de tales objetos. Los objetos pueden ser personas, objetos físicos o conceptos. Se representan mediante una Constante ( Letras minúsculas) , Variable( La primer letra es mayúscula) Las cualidades , relaciones o atributos , se denominan predicados . Los objetos se conocen como argumentos o términos del predicado .

6. Características de los Predicados Los predicados tienen asociado un valor de veracidad que resuelve a verdadero o falso , dependiendo de sus términos o argumentos . Es un mapeo de objetos al conjunto {0,1} Los predicados pueden ser usados para asignar una cualidad abstracta a sus términos o para representar acciones o relaciones de acción entre dos objetos. Al construir un predicado se asume que su veracidad está basada en su relación con el mundo real.

7. Ejemplo Pedro X José Y X X = { p edro, jose, X, Y} Relación José es el padre de Pedro Predicado padre( jose, pedro) es V o F depende del dominio del problema Mapeo padre: X x X ->{0,1}

8. Predicados, Axiomas y Patrones A los predicados cuyos argumentos representen a un objeto específico ( términos constantes ), que sean establecidos y asumidos como lógicamente verdaderos, se los denomina axiomas . A los predicados que tienen variables como argumentos , se los denomina patrones .

9. Átomo: Es la aplicación de un predicado a una lista de argumentos: Lista de argumentos: constante, variable, predicados, funciones padre ( jose, pedro) ama (jose, perro_de (jose)) Operadores :  ,V , ~, --> Cuántificadores :  ,  Expresión: Una expresión puede ser un atomo o una combinacion de atomos por medio de operadores o cuantificadores

10. Escribir las siguientes expresiones: Tomas es mas pequeño que Karen Jose es mas alto que Tomas Tanto Karen como Jaime son mas altos que Tomas Nadie es mas alto que Jaime Jose ama a su perro Pedro ama a todos sus perros Tomas golpeo a alguien que tenia un martillo Tomas golpeo a alguien y utilizo un martillo

11. Skolenización Elimina los cuantificadores Existenciales. a)  x  yQ(x,y)  x  y 1 ,y 2 ,..y n Q(x,y 1 ,y 2 , ..y n )  y 1 ,y 2 ,..y n Q(x 0 ,y 1 ,y 2 , ..y n ) x 0 es la constante de Skolen b)  y  x Q(x,y)  y 1 ,y 2, ..y n  x Q(x,y 1 ,y 2, . ..y n )  y 1 ,y 2 ,..y n Q(f(y 1 ,y 2 , ..y n ), y 1 ,y 2, . ..y n ) f es la función de Skolen

12. Ejemplo a) Existe al menos una casa que pertenece a todos b) Todos Tienen por lo menos una casa

13. Lógica de Predicados: La Unificación Para determinar la veracidad de sentencias compuestas por predicados y conectivos lógicos, es necesario evaluar la veracidad de cada uno de sus componentes y luego aplicar los operadores lógicos a los resultados. Un predicado componente resuelve a verdadero si se identifica con un axioma de la base de conocimiento. La unificación es un proceso que computa las sustituciones apropiadas para determinar si dos predicados coinciden o se identifican.

14. Lógica de Predicados: El Proceso de Unificación (1) Todo predicado que no contenga variables en sus argumentos, debe tener un axioma que se identifique totalmente, para considerarlo como verdadero. Si un predicado tiene una variable , ésta debe ser asociada a un valor determinado. Se seleccionan todos los axiomas de la base que se identifiquen con el patrón en todo excepto por la variable . La variable es asociada con el valor del argumento de la posición correspondiente del axioma .

15. Lógica de Predicados: El Proceso de Unificación (2) Si más de un axioma se identifica con el predicado dado, todos los valores asociados son considerados y tratados separadamente . El proceso de identificación continúa asumiendo que el valor de la variable es el valor asociado , en cualquier lugar que ésta aparezca. Los conectivos lógicos son aplicados a todos los predicados, para determinar la veracidad de la sentencia dada.

16. Elementos a considerar para Unificar Variable ligada : (v, exp) v: Variable exp : Cualquier Expresión: Constante, variable, predicado, función, conjunciones, disyunciones. Lista de variables ligadas : {(v, exp)} No debe haber variables ligadas repetidas Instanciación: p | σ p: exp y σ : lista de variables ligadas abogado (X) | σ ={(X, jose)}  abogado(jose)

17. Unificador mas general de 2 expresiones: p, q umg (p, q) Cuando al menos una de las 2 Ninguna de las 2 expresiones expresiones es una constante o variable es constante o variable a._Si al menos una de las expresiones Puede ser función, predicado es una variable, se liga la variable conjunciones, disyunciones a la otra expresión Deben ser mismo tipo, nombre σ ={(p, q)} y longitud (m) b. Si las dos expresiones son constantes k=1 σ = Φ idénticas mientras k<= m σ = Φ vacío σ ’ <- umg(p k | q k) c. Si las 2 expresiones son constantes distintas el proceso fallo σ <- σ ’ union σ fin mientras

18. Ejemplos 1) p: x q: jose 2) p: x q: casa_de( jose) 3) p: abogado (x) q: abogado (jose) 4) p: f (x, y) q: f (y, a)

19. La Normalización de una Expresión Algoritmo Eliminar  Introducir las negaciones a nivel atómico ~(a ^ b) ≡ ~a v ~b Variables con alcances diferentes deben tener nombres diferentes Eliminar los cuantificadores existenciales y mover los cuantificadores Universales a la izquierda Borrar prefijos Manipular hasta dejar conjunciones de disyunciones Separar los factores de las conjunciones Agrupar las negaciones Insertar el 

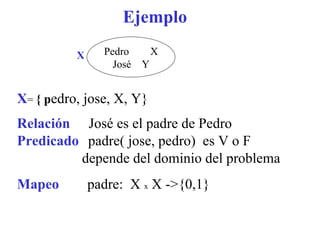
20. Ejemplo  c (grande(c)->mantenimiento(c) v [ ~  j jardin(j, c) ^  p limpiar (p,c)])

21. Problema#2 1. A Jhon le gusta toda clase de comida 2. Las manzanas son comida 3. El pollo es comida 4. Cualquier cosa que uno coma y no le mate es comida 5. Bill come cacahuates y aún esta vivo 6. Sue come todo lo que come Bill. ¿ A Jhon le gustan los cacahuates ? Usando la resolución, determine si la consulta es Verdadera