Este documento describe un experimento para verificar la caída libre y la aceleración de la gravedad. Se midió la velocidad de una rejilla y una rejilla con peso adicional al caer, encontrando que la aceleración de la gravedad es aproximadamente 9.75 m/s2 en la ciudad de La Paz con un margen de error del 3%. Adicionalmente, se comprobó que la aceleración no depende de la masa del objeto.

1. CAÍDA LIBRE
I. Objetivos
 Verificar el fenómeno de caída libre
 Comprobar el valor de la aceleración de la gravedad
 Verificar que la aceleración no depende de la masa de los cuerpos
libres
II. Marco teórico
En física, se denomina caída libre al movimiento de un cuerpo bajo la acción
exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las
caídas reales influenciadas en mayor o menor medida por la resistencia
aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un
fluido; sin embargo es frecuente también referirse coloquialmente a éstas como
caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general
despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente
sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o
a satélites en órbita alrededor de la Tierra o de cualquier otro cuerpo celeste.
Otros sucesos referidos también como caída libre lo constituyen las trayectorias
geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
III. Procedimiento
Figura 1 Figura 2
Rejilla
Fotopuerta
Detector
Haz Infrarrojo
Emisor
LED indicador
de obstrucción

2. 1) Se monto el arreglo de la figura 1, se conecto la fotopuerta a la entrada
DIG/SONIC 1 de la interfaz LabPro y luego a la computadora mediante un
cable USB.
2) Luego de iniciar el programa Logger Pro y se abrió el archivo 03caida
3) Se sujeto la rejilla por su parte superior por encima del detector de
movimiento como muestra la figura 1. Se activo el botón de “play” de la
barra de herramientas, luego de soltar la rejilla el programa tomo los datos.
En el programa Logger Pro se lleno la tabla “ t vs v” y los puntos (t.v) se
ubicaron en el grafico adyacente
4) Con los datos del programa llenamos la siguiente Tabla 1
t (s) V (m/s)
2.1853 0.943
2.2046 1.130
2.2211 1.291
2.2358 1.434
2.2491 1.564
5) Medimos la rejilla de m1 = 150g , y luego se le añadió un peso más, lo que
nos dio una masa total de la rejilla y la pesa de m2=200g
6) Se realizo con la m2 el mismo procedimiento que el de la m1, obteniendo
una Tabla 2
t (s) V (m/s)
0.366 1.081
0384 1.249
0.399 1.396
0.412 1.530
0.425 1.653

3. IV. Tratamiento de datos
1) En base de la Tabla 1 se grafico los puntos experimentales y la regresión
lineal con intersección no nula con la relación v= f (t)
n X=t Y=v xy X^2 y¡
(y¡)^2
1 2.1853 0.943 2.061 4.775 -0.00177 3.1329*10^-6
2 2.2046 1.130 2.491 4.860 -0.0005362 2.875*10^-7
3 2.2211 1.291 2.867 4.933 -0.0006117 3.7417*10^-7
4 2.2358 1.434 3.206 4.999 -0.0002426 5.885*10^-8
5 2.2491 1.564 3.517 5.058 -0.0005277 2.7847*10^-7
n  

 
  4.1319*10^-6
푉 = 푉º + 푔푡
푌 = 퐴 + 퐵푥
Para A:
퐴 =
(6.362)(24.626) − (11.096)(14.143)
5(24.626) − (11.096)
퐴 = −20.372
Para B
퐵 =
5(14.143) − (11.096)(6.362)
5(24.626) − (11.096)
B = 9.753
Y=-20.372+9.753X

4. Para el grafico1 mediante Excel:
1.7
1.6
1.5
1.4
1.3
1.2
1.1
1
0.9
Velocidad vs Tiempo
2) Para determinar el intervalo de confianza de la pendiente, a un nivel de
confianza de 98%
Para el S(x/y):
y¡= (A+Bx¡)-y¡
푆(푥/푦) = √
Σ 훿푦2
푛 − 2
(4.1319 ∗ 10−6 )
푆(푥/푦) = √
5 − 2
푆(푥/푦) = 0.00117
y = 9.7346x - 20.33
R² = 1
0.8
2.18 2.2 2.22 2.24 2.26
Velocidad (m/s)
Tiempo (s)
velocidad (m/s)
Linear (velocidad
(m/s))

5. Para SB:
푆(퐵) =
푆(푥/푦)
√Σ 푥 2 −
(Σ 푥)2
푛
푆(퐵) =
0.00117
√24.626 −
(11.0959)2
5
푆(퐵) =0.0249
퐵 = 퐵̅ ± 푡
∝
2
푆(퐵)
퐵 = 9.75 ± 0.0249 ∗ 4.541
퐵 = 9.753 ± 0.113
Para el grafico 2 mediante Excel:
y = 9.7794x - 2.5018
R² = 0.9995
1.7
1.6
1.5
1.4
1.3
1.2
1.1
1
0.9
velocidad (m/s)
0.36 0.38 0.4 0.42 0.44
velocidad (m/s)
Linear (velocidad
(m/s))

6. 3) Para la gravedad
푔 = 9.753 ± 0.113
4) En base de la Tabla 2 de la Hoja de Datos, mediante un análisis de
regresión lineal con intersección no nula determinamos la relación
experimental v= (t) y dibujando junto con los puntos experimentales.
t (s) V (m/s)
0.366 1.081
0.384 1.249
0.399 1.396
0.412 1.530
0.425 1.653
Para la determinación de la relación experimental utilizaremos la calculadora
(algebra fx 2.0 plus), luego de introducir los datos tenemos que:
n X=t Y=v xy X^2
1 0.366 1.081 0.396 0.134
2 0.384 1.249 0.479 0.147
3 0.399 1.396 0.557 0.159
4 0.412 1.530 0.630 0.169
5 0.425 1.653 0.702 0.181
5  


퐵 = 9.751
퐴 = −2.491
Entonces tenemos que :
푉 = 푉º + 푔푡
푌 = 퐴 + 퐵푥
푦 = −2.491 + 9.751푥

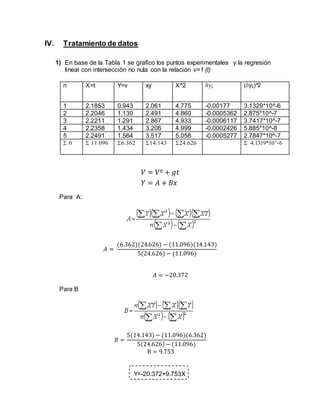
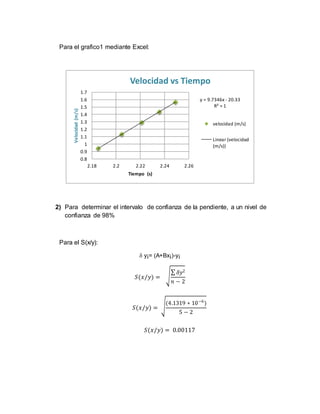
7. 5) Determinamos el intervalo de confianza de la pendiente de la relación
experimental v=(t), a un nobel de confianza de 98%.
Para desviación:
1
푛 − 2
푆(퐵) = √
[(
푆(푦)
푆(푥)
)
2
− ̅퐵̅̅̅2]
1
5 − 2
푆(퐵) = √
[(
0.226
0.023
)
2
− 9.7512]
푆(퐵) = 0.695
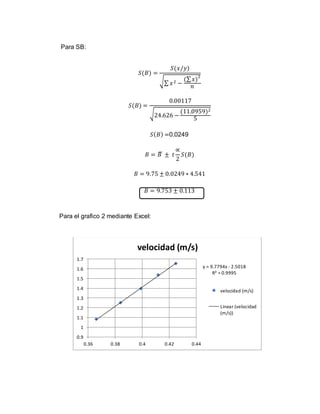
Para el intervalo de confianza:
퐵 = 퐵̅ ± 푡푐 푆(퐵)
퐵 = 9.751 ± 3.16
6) Dada la ecuación anterior, con el resultado del punto anterior escribir el
intervalo de confianza de “g”, a un nivel de confianza de 98%
푔 = 9.751 ± 3.16
7) Luego se calculo la diferencia porcentual de m2 respecto a m1. Calcular la
diferencia porcentual del valor medio de g , obtenido para m2, respecto del
obtenido para m1.
150 − 200
%퐷 = |
200
| ∗ 100%
%퐷 = 25.00%

8. V. CUESTIONARIO.
1. Si la rejilla se suelta desde el reposo ¿Por qué el punto 1- del tratamiento
de datos se hace un análisis de regresión lineal con intersección no nula ?
R.- En matemáticas, una familia de conjuntos F tiene la propiedad de
la intersección finita si la intersección de toda subfamilia de F finita y no
vacía tiene intersección no nula. Es dicer que si existía una velocidad
inicial.
2. Para la rejilla sola, ¿se probo a hipótesis de que el valor de g es 9.78 (m/
s2), a un nivel de confianza del 98% ? explicar
R.- Si se comprobó, porque el valor de la ctte B dio 9.75 (m/푠2) con un
margen de error mínimo, la variación de 9.75 (m/푠2) se debe al lugar del
experimento (cuidad de La Paz) que se encuentra a 3650 msnm (metros
sobre el nivel del mar).
3. Para la rejilla con peso , ¿se probo a hipótesis de que el valor de g es
9.78 (m/s2), a un nivel de confianza del 98% ? explicar
R.- Si se comprobó porque el valor de la ctte B dio 9.75 (m/푠2 ) con un
margen de error mínimo, la variación de 9.75 (m/푠2) se debe al lugar del
experimento (cuidad de La Paz) que se encuentra a 3650 msnm (metros
sobre el nivel del mar).
4. Se verifico que la aceleración no depende de la masa de los cuerpos en
caída libre? Explicar
R.- si se verifico la gravedad no depende de la masa, mas bien se
considero que la masa amplifica a la gravedad. Ya que en las dos tablas
dio como resultado el mismo valor de la aceleración gravitacional.
5. ¿Por qué una pluma cae más lentamente que un perdigón de la misma
masa?

9. R.- se debe a la fuerza del aire, que produce diferente resistencia en los
cuerpos
VI. CONCLUSIONES
 Se concluyo que la aceleración gravitacional no depende de la masa.
Pero varía dependiendo del lugar donde se realiza por ejemplo en la
ciudad de La Paz la gravedad resulto ser de 9.75 (푚
푠2).
 Que existe fuerzas externas como del aire que pueden afectar los
resultados a la hora de la caída libre.
 Se compro que es una intersección no nula debido a que éxite una
velocidad inicial
VII. BIBLIOGRAFÍA
Sitios web:
 http://rinconmatematico.com/foros/index.
 http://es.wikipedia.org/wiki/
 http://fisicacinematicadinamica.blogspot.com