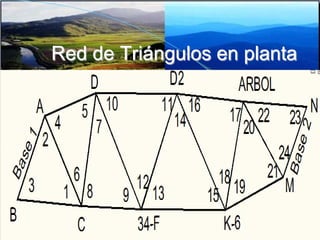
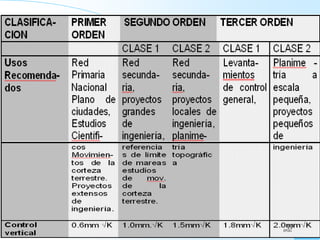
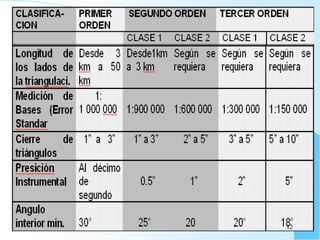
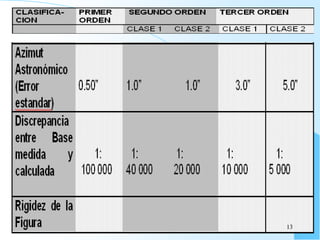
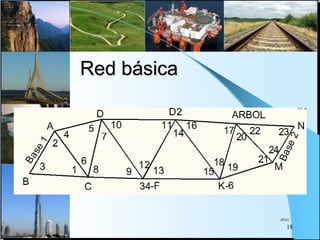
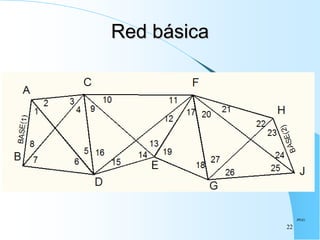
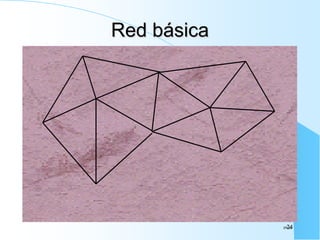
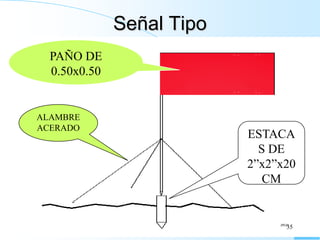
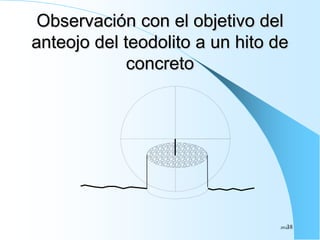
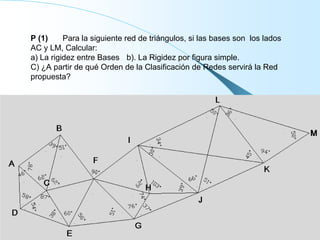
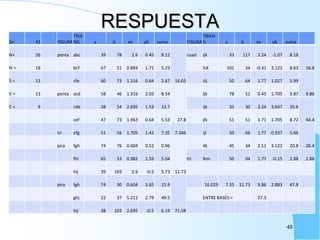
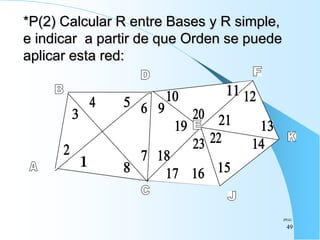
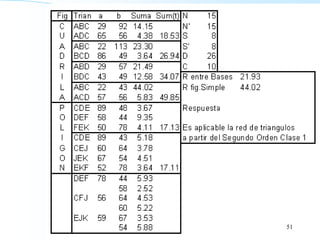
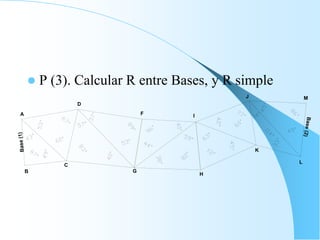
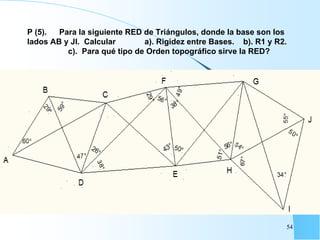
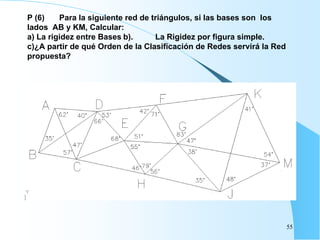
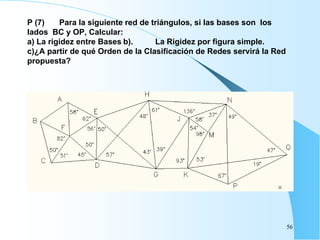
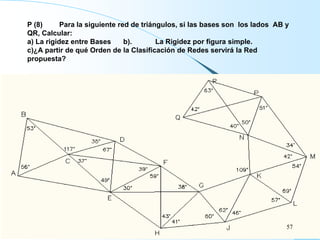
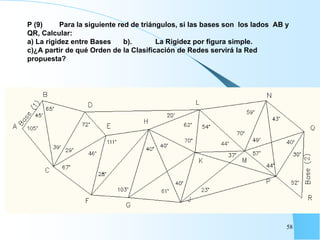
El documento proporciona información sobre triangulación topográfica. Explica los conceptos clave de triangulación como la formación de redes de triángulos, cuadriláteros y figuras con vértice central. También describe las etapas de una triangulación como el reconocimiento del terreno, señalización de vértices, medición de ángulos y bases, y cálculo de coordenadas. Además, incluye ejemplos y problemas de cálculo de rigidez en redes de triangulación.

1. TOPOGRAFIA II
Mgt. Ing. Juan Pablo
Gamarra Góngora
2013

2. CAPITULO 1
TRIANGULACION

3.  Generalidades
 La triangulación es el
procedimiento que se emplea para el
control de levantamientos extensos,
con una precisión de acuerdo al
objetivo que se persiga, y está
formada por una cadena de
triángulos en que uno o mas lados
de cada triángulo lo son de otros, y
la intersección de los lados son
vértices de la triangulación. 3

4.  La triangulación ha sido el
método más eficaz para lograr una
red precisa sobre grandes áreas
debido a que es posible medir los
ángulos con precisión a lo largo de
grandes tramos, aun cuando el
acceso directo entre los puntos
resulte difícil.
JPGG 4

5. Formación de la red
JPGG
5

6.  La característica fundamental de la
triangulación es que se pueden medir todos los
ángulos de una red de triángulos y el cálculo de
todos los lados se realizan utilizando los
métodos de la trigonometría plana o esférica a
partir de una línea base principal, medida con
mucha precisión y precauciones y
refinamientos requeridos.
6

7. Red de Triángulos en planta
JPGG
7

8. Aplicaciones de la Triangulación
 La triangulación es base
fundamental y necesaria para
ciertos trabajos topográficos de
precisión como son:
 Apoyo para los levantamientos y
construcción de puentes, presas,
carreteras, líneas férreas, líneas
de conducción, etc.
 Los planos topográficos de una
ciudad o de una zona montañosa
donde la poligonación sería lenta y
difícil. 8

9.  Control superficial y subterráneo
tanto en minas como la
construcción de túneles y
lumbreras.

 Apoyo terrestre para los vuelos
fotogramétricos.
 Los mapas y planos topográficos
de una gran extensión y de
superficie accidentada.
9

10. Clasificación de las
Triangulaciones
2013

11. JPGG
11

12. 12

13. 13

14. JPGG
14

15. Redes de Figuras
Geométricas.-
 Red de Triángulos
 Red de Cuadriláteros
 Red de Figuras con vértice
central
15

16. Red de Triángulos.-
 Es una cadena formada por
triángulos, se emplea cuando el
terreno a levantar no requiere de
mucha precisión, es propicio para
proyectar una carretera, una línea
férrea, canales de irrigación, etc,
generalmente para levantamientos
longitudinales,
16

17. Red de Triángulos.-
 donde necesariamente se miden
dos bases y todos los ángulos en
cada vértice (cierre al horizonte),
de tal manera que con estos datos
se puedan calcular todos los lados
de la triangulación.
17

18. Red básica
JPGG
18

19. Red de Cuadriláteros
 Este tipo de figura se emplea
generalmente para levantar terrenos
que requieran alta precisión, como
por ejemplo para proyectar un túnel,
un puente, etc. O cuando se ha de
proyectar una carretera, línea férrea u
otra obra de importancia.
19

20. Red de Cuadriláteros
 Se miden una base y otra de
comprobación después de 20 figuras
semejantes,, así mismo se miden
todos los ángulos (se recomienda)
en cada vértice.
20

21. Red básica
JPGG
21

22. Red básica
JPGG
22

23. Red de Figuras de Vértice
Central
 Se escoge este tipo de figura
generalmente para abarcar grandes
extensiones de terreno, así mismo
cuando es imposible trazar un
cuadrilátero o cuando sus estaciones
de triangulación no son ínter visibles.
Figura empleada para levantamientos
de terrenos en irrigaciones.
23

24. Red básica
JPGG24

25. QUE TIPO DE REDES
PLANTEAMOS PARA LAS
SIGUIENTES OBRAS
CIVILES?

26. 26
FASES DE UNA
TRIANGULACIÓN

27.  1. Reconocimiento del terreno.
 2. Señales de los vértices.
 3. Rigidez de las redes.
 4. Medida de los ángulos horizontales y
verticales.
 5. Medida de bases.
 6. Compensaciones.
 7. Cálculo de las coordenadas UTM de los
vértices.
 8. Rellenos
 9. Dibujo de Planos 27

28. 28
1. RECONOCIMIENTO DEL
TERRENO

29.  - Selección de los vértices.- Es
recomendable que haya visibilidad entre
ellos a largas distancias, así mismo
cuando la precisión así lo requiera se
pueden escoger dentro de una ciudad el
remate de las cúpulas de las torres de
iglesias, depósitos elevados de agua o
construir torres elevadas en lugares
montañosos. 29

30.  - Acceso a los vértices o estaciones.- No
deben construirse estaciones en propiedades
privadas, salvo cuando se tenga la autorización
respectiva del propietario.
30

31.  - Determinar la forma de los
triángulos.- Es preferible escoger
triángulos equiláteros como figuras bases,
pero si esto no es posible los ángulos
internos de los triángulos tengan por lo
menos de 30 a 150 , pero no menores a
20 ni mayores a 150 ya que el logaritmo
de estos ángulos varia muy rápidamente
cuando se acercan mas a los 0 ó a los
180 . Para la medida de ángulos se utiliza
la brújula y para las distancias el
podómetro o el GPS. 31

32.  - La conveniencia de Medición de
Bases.- Si uno de los lados del triángulo
va ser una base, esta deberá estar
ubicado en una planicie, si ha de medirse
con cinta metálica, pero no así si ha de
medirse con distanciómetro.
32

33. 33
2. SEÑALES DE LOS
VÉRTICES

34.  En cada estación o vértice de triangulación
se establece una señal que sea visible
desde aquellos puntos desde donde ha de
observarse.
 El tamaño del paño (d) se determina con
la siguiente fórmula d = 0.0004D, donde D
es la distancia entre los vértices.
 Para distancias muy largas donde el
tamaño del paño sería muy grande, se
utilizan los heliotropos, instrumentos que
trabajan con la ayuda del sol.
34

35. Señal Tipo
ESTACA
S DE
2”x2”x20
CM
ALAMBRE
ACERADO
PAÑO DE
0.50x0.50
JPGG
35

36. Tipos de estacas mas comunes
JPGG36

37.  Pero cuando la estación ha de
utilizarse durante mucho
tiempo se señala el vértice con
un hito de concreto, colocando
en vez del clavo un fierro
corrugado de ½”.
37

38. Observación con el objetivo del
anteojo del teodolito a un hito de
concreto
JPGG38

39. Distribución en el campo
JPGG
39

40. Medida preliminar de los ángulos
de la Red
 1. Con Brújula Brunton
Se miden todos los azimutes de los lados de la
red de triángulos y se deducen los ángulos
internos de la figura.
 2. Con GPS
Se anotan las coordenadas geográficas que dan
un GPS colocado en cada estación y se
calculan los ángulos internos de la Red.
JPGG
40

41. 41
3. RIGIDEZ DE LAS REDES

42. La rigidez ó consistencia (R) de una figura, es
una cantidad adimensional que permite
cuantificar la calidad trigonométrica de
cualquier red de triángulos. Por lo tanto, indica
el número de figuras geométricas que se
pueden formar en un itinerario longitudinal . La
rigidez esta controlada por la amplitud de los
ángulos internos de las figuras geométricas, y
esta amplitud depende del orden en cual se
esta trabajando.
42

43.  La consistencia de la red se calcula
con la siguiente relación:
 D - C
 R= ----------- (δa2 +δb2 +δaδb )
 D
 donde:
 D = Número total de lados observados en
cada estación sin considerar la Base ó
Bases. JPGG43

44. C=(N-2S+3)+(N’-S’+1)
 C = Número de condiciones de ANGULO y
LADO que han de ser satisfechas en la red
desde la línea conocida hasta el lado en
cuestión.
 N = Número total de lados de la red.
 N'= Número total de lados que han sido
observados en ambas direcciones.
 S = Número total de estaciones.
 S'= Número total de estaciones ocupadas. 44

45.  δa, δb: Suma de los senos de los
ángulos en la sexta cifra decimal
correspondientes a los ángulos opuestos
al lado conocido (A) y al lado por conocer
(B).
45

46. Triangulación
PROBLEMAS
46

47. P (1) Para la siguiente red de triángulos, si las bases son los lados
AC y LM, Calcular:
a) La rigidez entre Bases b). La Rigidez por figura simple.
C) ¿A partir de qué Orden de la Clasificación de Redes servirá la Red
propuesta?
47

48. RESPUESTA
D= 41 FIGURA
TRIA
NG a b xa yb suma FIGURA
TRIAN
G a b xa yb suma
N= 26 penta abc 39 78 2.6 0.45 8.12
16.03
cuad ijk 33 117 3.24 -1.07 8.18
16.8N´= 18 bcf 67 51 0.894 1.71 5.23 ILK 101 34 -0.41 3.122 8.63
S = 13 cfe 60 73 1.216 0.64 2.67 IJL 50 64 1.77 1.027 5.99
9.86S´= 13 penta acd 58 46 1.316 2.03 8.54
27.8
ljk 78 51 0.45 1.705 3.87
C = 9 cde 38 54 2.695 1.53 13.7 ijk 33 30 3.24 3.647 35.6
44.4cef 47 73 1.963 0.64 5.53 jlk 51 51 1.71 1.705 8.72
tri efg 51 56 1.705 1.42 7.35 7.346 ijl 50 66 1.77 0.937 5.66
26.4pira fgh 74 76 0.604 0.52 0.96
11.73
ilk 45 34 2.11 3.122 20.8
fhi 65 53 0.982 1.59 5.04 tri lkm 50 94 1.77 -0.15 2.88 2.88
hij 39 103 2.6 -0.5 5.73
pira fgh 74 30 0.604 3.65 15.9
71.58
16.029 7.35 11.73 9.86 2.883 47.8
ghj 22 37 5.211 2.79 49.5 ENTRE BASES = 37.3
hij 38 103 2.695 -0.5 6.19
48

49. *P(2) Calcular R entre Bases y R simple,
e indicar a partir de que Orden se puede
aplicar esta red:
JPGG
49

50.  1 = 56º; 2 = 57º; 3 = 43º; 4 = 49º;
 5 =29º; 6 = 57º; 7 = 43º; 8 = 22º;
 9 = 43º;10 = 44º; 11 = 58º; 12 = 52º;
 13 = 50º; 14 = 67º; 15 = 54º; 16 = 60º;
 17 = 64º; 18 = 48º; 19 = 89º; 20 = 78º;
 21 = 78º; 22 = 59º; 23 = 56º.
 Si las bases son los lados:
 a.- AB y FK. b.- AB y JK. c.- AB y EK
50
Si los ángulos medidos son:

51. 51

52.  P (3). Calcular R entre Bases, y R simple
A
B
D
C
F
G
I
H
J
K
M
L
Base(1)
Base(2)

53. P (4) Para que Orden de la Clasificación se
puede utilizar esta Red, Si las Bases fuesen:
 a) AA1 y A16A17 b) AA4 y A14A17

54. P (5). Para la siguiente RED de Triángulos, donde la base son los
lados AB y JI. Calcular a). Rigidez entre Bases. b). R1 y R2.
c). Para qué tipo de Orden topográfico sirve la RED?
54

55. P (6) Para la siguiente red de triángulos, si las bases son los
lados AB y KM, Calcular:
a) La rigidez entre Bases b). La Rigidez por figura simple.
c)¿A partir de qué Orden de la Clasificación de Redes servirá la Red
propuesta?
55

56. P (7) Para la siguiente red de triángulos, si las bases son los
lados BC y OP, Calcular:
a) La rigidez entre Bases b). La Rigidez por figura simple.
c)¿A partir de qué Orden de la Clasificación de Redes servirá la Red
propuesta?
56

57. P (8) Para la siguiente red de triángulos, si las bases son los lados AB y
QR, Calcular:
a) La rigidez entre Bases b). La Rigidez por figura simple.
c)¿A partir de qué Orden de la Clasificación de Redes servirá la Red
propuesta?
57

58. P (9) Para la siguiente red de triángulos, si las bases son los lados AB y
QR, Calcular:
a) La rigidez entre Bases b). La Rigidez por figura simple.
c)¿A partir de qué Orden de la Clasificación de Redes servirá la Red
propuesta?
58