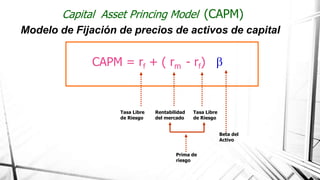
El documento presenta información sobre el Modelo de Fijación de Precios de Activos de Capital (CAPM). El CAPM es un modelo utilizado para determinar la tasa de rentabilidad teóricamente requerida para un activo al agregarlo a una cartera diversificada. Toma en cuenta el riesgo sistémico de mercado (beta), la tasa libre de riesgo y la rentabilidad esperada del mercado. Se asumen supuestos como inversionistas aversos al riesgo y equilibrio en el mercado. La fórmula del CAPM es la tasa de

1. CAPM
Ricardo Medina González
miércoles, 2 de noviembre de 2016

2. Administración de Riesgos Financieros
Riesgo y Rendimiento
miércoles, 2 de noviembre de 2016

3. CAMP

4. •(trad. lit. Modelo de Fijación de precios de activos de capital) es un
modelo frecuentemente utilizado en la economía financiera.
•El modelo es utilizado para determinar la tasa de rentabilidad
teóricamente requerida para un cierto activo, si éste es agregado a
un portafolio adecuadamente diversificado y a través de estos datos
obtener la rentabilidad y el riesgo de la cartera total.
•El modelo toma en cuanto la sensibilidad del activo al riesgo no-
diversificable (conocido también como riesgo del mercado o riesgo
sistémico, representado por el símbolo de beta (β), así como
también el rentabilidad esperado del mercado y el rentabilidad
esperado de un activo teóricamente libre de riesgo.
CAMP

5. Para la construcción del Modelo CAPM se asumen los
siguientes supuestos:
* los inversionistas son personas adversas al riesgo
* los inversionistas cuidan el equilibrio entre el retorno
esperado y la variabilidad asociada para conformar sus
portafolio
* No existen fricciones o fallas en el mercado
* Existe una tasa libre de riesgo a las cuales los
inversionistas pueden endeudarse o colocar fondos
* No existe asimetría de la información y los inversionistas
son racionales, lo cual no implica que todos los
inversionistas tienen las mismas conclusiones acerca de los
retornos esperados y de las desviaciones estándar de los
portafolios factibles.

6. El CAPM se utiliza para determinar la tasa de retorno esperada de un activo. En el
equilibrio, si está agregado a una Cartera de inversiones adecuadamente
diversificada, será capaz de ubicarse en cualquier punto a lo largo de la línea roja,
conocida como la Línea del Mercado de Capitales. Al igual que en el modelo de
Markowitz, a medida que el inversionista corre mayor riesgo (desplazamiento hacia
la derecha) obtiene un mayor retorno esperado. El CAPM toma en cuenta la
sensibilidad del activo al riesgo no-diversificable, conocido como riesgo de
mercado o riesgo sistémico, representado por el símbolo de Beta (β), así como
también el retorno esperado del mercado y el retorno esperado de un activo
teóricamente libre de riesgo.

7. De acuerdo a la gráfica:
• E(ri) es la tasa de rendimiento esperada de capital sobre el
activo i.
• βim es el Beta (cantidad de riesgo con respecto al Portafolio
de Mercado)
• E(rm − rf) es el exceso de rentabilidad del portafolio de
mercado.
• (rm) Rendimiento del mercado.
• (rf) Rendimiento de un activo libre de riesgo.

8. Debemos tener presente que se trata de un Beta no
apalancado, que supone que la empresa no tiene deuda
en su estructura de capital, por lo tanto no se incorpora el
riesgo financiero propio. En caso de querer incorporarlo,
ha que determinar un Beta apalancado; por lo tanto el
rendimiento esperado será más alto. En este caso el Beta
apalancado permite calcular el costo del capital.

9. FÓRMULA
𝐄 𝒓𝒊 = 𝒓 𝒇 + 𝜷(𝒓 𝒎 − 𝒓 𝒇)
Donde:
• E(ri) es la tasa de rendimiento esperada de capital
sobre el activo i.
• β es el Beta (cantidad de riesgo con respecto al
Portafolio de Mercado)
• (rm − rf) es el exceso de rentabilidad del portafolio
de mercado.
• (rm) Rendimiento del mercado.
• (rf) Rendimiento de un activo libre de riesgo.

10. CAPM = rf + ( rm - rf)
Capital Asset Princing Model (CAPM)
Tasa Libre
de Riesgo
Rentabilidad
del mercado
Tasa Libre
de Riesgo
Beta del
Activo
Prima de
riesgo
Modelo de Fijación de precios de activos de capital

11. Ejemplo
•

12. EJERCICIO.
A. Calcule la beta de cada activo.
B. Calcule la beta de la cartera de los tres
activos suponiendo la siguiente proporción de
inversión:
Coca cola 30% Apple 40% Sony 30%.
C. Cálculo de CAMP para cada activo
suponiendo que la rf es cetes 4.87% a un año

13. S&P KO AAPL SNE
Date Adj Close RENDIMIENTO Adj Close RENDIMIENTO Adj Close RENDIMIENTO Adj Close RENDIMIENTO
19/09/2016 26.2200 1.1574 42.740002 1.4238 112.7100 -1.923 33.6000 5.6936
12/09/2016 25.9200 0.4261 42.139999 0.5069 114.9200 11.4321 31.7900 -2.0338
06/09/2016 25.8100 -2.0865 41.927456 -3.1836 103.1300 -4.2699 32.4500 -0.5821
29/08/2016 26.3600 0.3044 43.30619 0.7848 107.7300 0.7387 32.6400 -1.6274
22/08/2016 26.2800 -0.277 42.968945 -1.3661 106.9400 -2.2128 33.1800 1.4058
15/08/2016 26.3530 0.0493 43.564083 -0.2498 109.3600 1.0907 32.7200 -0.3046
08/08/2016 26.3400 1.1792 43.673191 1.2649 108.1800 0.6512 32.8200 0.3056
01/08/2016 26.0330 -0.5538 43.127651 -0.3438 107.4800 3.6966 32.7200 -2.0652
25/07/2016 26.1780 0.0611 43.276436 -4.8003 103.6485 5.6253 33.4100 10.5925
18/07/2016 26.1620 0.8558 45.458607 0.4383 98.1284 -0.1214 30.2100 0.5659
11/07/2016 25.9400 1.7654 45.260227 0.5509 98.2478 2.1721 30.0400 -1.7979
05/07/2016 25.4900 1.3801 45.012253 0.5762 96.1591 0.8238 30.5900 4.083
27/06/2016 25.1430 2.1657 44.75436 2.7088 95.3733 2.6659 29.3900 6.4855
20/06/2016 24.6100 -0.2432 43.574005 -1.92 92.8968 -2.0245 27.6000 -1.1461
13/06/2016 24.6700 -2.2195 44.427036 -1.8623 94.8164 -3.5414 27.9200 -0.3924
06/06/2016 25.2300 -0.1582 45.270145 2.1092 98.2975 0.9293 28.0300 0.2862
31/05/2016 25.2700 0.1982 44.335014 0.5806 97.3924 -2.4215 27.9500 -0.2498
23/05/2016 25.2200 2.2294 44.079082 1.8885 99.8093 5.3875 28.0200 5.9757
16/05/2016 24.6700 0.3661 43.262077 -3.087 94.7070 5.1922 26.4400 1.2251
09/05/2016 24.5800 -0.0691 44.64016 0.0661 90.0323 -2.3727 26.1200 9.426
02/05/2016 24.5970 -0.8585 44.610634 1.1607 92.2204 -0.4859 23.8700 -0.9543
26/04/2016 24.8100 .------. 44.09877 .------. 92.6707 .------. 24.1000 .------.

14. Por su atención…
¡Gracias!

15. ¿Dónde encontramos la tasa libre de
riesgo: rf?
Reporte semanal del Scotiabank
rf CORTO PLAZO : Letras T-Bill
LARGO PLAZO : Bonos T-Bond
Damodaram
www.bondsonline.com

16. Annual Returns on Stock, T.Bonds and T.Bills: 1928 - Current
The raw data for treasury bond and bill returns is obtained from the Federal Reserve database in St. Louis (FRED). The treasury bill rate is a 6-month rate and the trreasury bo
Year Stocks T.Bills T.Bonds Stocks T.Bills T.Bonds
1928 43.81% 3.08% 0.84% $143.81 $103.08 $100.84
1929 -8.30% 3.16% 4.20% $131.88 $106.34 $105.07
1930 -25.12% 4.55% 4.54% $98.75 $111.18 $109.85
1931 -43.84% 2.31% -2.56% $55.46 $113.74 $107.03
1932 -8.64% 1.07% 8.79% $50.66 $114.96 $116.44
1933 49.98% 0.96% 1.86% $75.99 $116.06 $118.60
1934 -1.19% 0.30% 7.96% $75.09 $116.41 $128.05
1935 46.74% 0.23% 4.47% $110.18 $116.68 $133.78
1936 31.94% 0.15% 5.02% $145.38 $116.86 $140.49
1937 -35.34% 0.12% 1.38% $94.00 $117.00 $142.43
1938 29.28% 0.11% 4.21% $121.53 $117.12 $148.43
Annual Returns on Investments in Compounded Value of $ 100
2005 4.85% 4.31% 2.87% $146,062.54 $1,892.09 $4,455.50
2006 15.63% 4.88% 1.96% $168,886.53 $1,984.43 $4,542.87
Risk Premium
Arithmetic Average Stocks - T.BillsStocks - T.Bonds
1928-2006 11.77% 3.90% 5.20% 7.87% 6.57%
1966-2006 11.61% 6.03% 7.48% 5.57% 4.13%
1996-2006 11.06% 4.15% 5.92% 6.91% 5.14%
Risk Premium
Geometric Average Stocks - T.BillsStocks - T.Bonds
1928-2006 9.86% 3.85% 4.95% * 6.01% 4.91%
1966-2006 10.34% 6.00% 7.08% 4.34% 3.25%
1996-2006 9.56% 4.14% 5.67% 5.42% 3.90%
*=ES LA QUE SE TOMA EN CUENTA PARA LA VALORIZACION
www.damodaram on line

17. Industry Name
Advertising 36 0.99 22.25% 11.96% 0.83 6.85% 0.89
Aerospace/Defense 73 0.92 20.81% 21.77% 0.79 6.35% 0.84
Air Transport 56 1.38 42.16% 19.40% 1.03 11.95% 1.17
Apparel 64 0.93 13.39% 21.60% 0.84 5.46% 0.89
Auto & Truck 31 1.29 125.80% 18.90% 0.64 11.63% 0.72
Auto Parts 64 0.99 52.49% 18.93% 0.69 9.69% 0.77
Bank 550 0.59 54.59% 27.81% 0.43 10.20% 0.47
Bank (Canadian) 7 0.72 10.07% 24.41% 0.67 4.78% 0.7
Bank (Foreign) 4 1.78 NA 0.00% NA NA NA
Bank (Midwest) 37 0.79 61.47% 29.14% 0.55 8.86% 0.61
Beverage (Alcoholic) 27 0.66 23.56% 15.30% 0.55 1.67% 0.56
Beverage (Soft Drink) 21 0.71 13.63% 17.74% 0.63 3.75% 0.66
Biotechnology 105 1.56 4.39% 4.41% 1.5 6.65% 1.61
Building Materials 47 0.98 33.54% 23.55% 0.78 14.48% 0.91
Cable TV 23 1.76 38.89% 13.90% 1.31 2.42% 1.35
Canadian Energy 14 0.73 14.27% 30.19% 0.66 1.28% 0.67
Cement & Aggregates 13 1.02 26.35% 26.29% 0.85 2.61% 0.87
Chemical (Basic) 24 0.98 27.64% 13.31% 0.79 5.08% 0.83
Chemical (Diversified) 36 0.97 16.32% 25.87% 0.86 3.74% 0.9
Chemical (Specialty) 94 0.98 21.54% 19.08% 0.84 3.25% 0.87
Coal 16 1.75 15.96% 11.64% 1.53 4.11% 1.6
Computer Software/Svcs 425 1.84 3.56% 10.36% 1.79 10.49% 2
Computers/Peripherals 148 1.99 6.68% 7.84% 1.88 12.11% 2.14
Diversified Co. 134 0.87 22.60% 18.87% 0.74 5.95% 0.79
Drug 334 1.59 9.36% 6.09% 1.46 8.53% 1.6
E-Commerce 60 2.23 3.86% 9.38% 2.15 14.00% 2.5
Educational Services 37 1.09 2.65% 20.95% 1.06 8.99% 1.17
Electric Util. (Central) 24 0.94 69.87% 26.93% 0.62 1.66% 0.63
Electric Utility (East) 29 0.87 56.29% 28.01% 0.62 1.26% 0.63
Electric Utility (West) 16 0.97 58.80% 28.87% 0.68 3.26% 0.71
Electrical Equipment 94 1.52 72.60% 15.47% 0.94 7.73% 1.02
Electronics 186 1.49 14.54% 13.04% 1.33 14.11% 1.54
Entertainment 101 1.3 26.12% 16.69% 1.07 4.53% 1.12
Entertainment Tech 31 2.18 3.38% 10.21% 2.12 16.90% 2.55
Environmental 96 0.87 48.22% 9.45% 0.6 2.14% 0.62
Financial Svcs. (Div.) 269 0.89 132.40% 19.72% 0.43 6.92% 0.47
Food Processing 123 0.72 22.39% 19.60% 0.61 2.53% 0.63
Food Wholesalers 21 0.72 29.15% 23.66% 0.59 5.02% 0.62
Foreign Electronics 10 1.03 23.76% 41.66% 0.9 15.59% 1.07
Furn/Home Furnishings 38 0.87 30.22% 26.93% 0.71 4.45% 0.75
Grocery 19 1.04 39.11% 23.54% 0.8 5.43% 0.84
Healthcare Information 34 1.22 10.30% 10.07% 1.12 8.50% 1.22
Home Appliance 14 0.84 18.39% 14.69% 0.73 11.22% 0.82
Homebuilding 41 0.98 61.74% 23.77% 0.67 5.51% 0.71
Hotel/Gaming 84 0.77 33.19% 14.22% 0.6 2.99% 0.62
Household Products 31 0.79 18.46% 24.86% 0.69 2.74% 0.71
Unlevered
Beta
Cash/Firm
Value
Unlevered Beta
corrected for cash
Number of
Firms
Average Beta
Market D/E
Ratio
Tax Rate
¿y el beta del sector?
Archivo Betas Aswath Damodaran
http://pages.stern.nyu.edu/~adamodar/New_Home_Page/datafile/Betas.html
*=Beta apalancado

18. ¿y el beta del sector?
Archivo Betas Aswath Damodaran
http://pages.stern.nyu.edu/~adamodar/New_Home_Page/datafile/Betas.html
Hay que
trabajar con
la Beta
apalancada
IndustryName
Hotel/Gaming 84 0.77 33.19% 14.22% 0.6 2.99% 0.62
Unlevered
Beta
Cash/Firm
Value
UnleveredBeta
correctedforcash
Numberof
Firms
AverageBeta
MarketD/E
Ratio
TaxRate
Be=Beta apalancada=Beta Patrimonial=Beta desampalancada x(1+(1-t)*(Pasivo/Patrimonio)
Boa=Beta Económico=Beta Desampalacada=Beta sin Deuda= Be
(1+(1-T)(D/C)

19. ¿Dónde encontramos la tasa de
mercado : rm ?
http://www.marketreturnbenchmark.com/
Benchmark 2006
2007
YTD
(10/31/
07)
3 Year
Annlzd.
5 Year
Annlzd.
Market Return
Benchmark
20.90% 12.92% 19.26% 21.81%
S&P 500 Index 15.80% 10.87% 13.16% 13.88%
JWA market return Benchmark Results

20. ¿Dónde encontramos el
riesgo país?
Reporte semanal del BCP AL 121208 = 451 PUNTOS: 4.5

21. Por su atención…
¡Gracias!