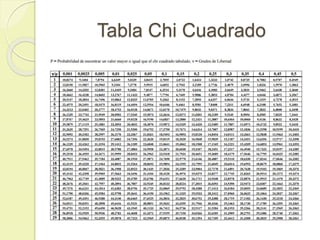
Se analiza la relación entre el consumo de tabaco y el sexo utilizando el estadístico chi cuadrado, formulando hipótesis nula (h0) y alternativa (h1). A través de frecuencias observadas y esperadas, se determina que el valor calculado de chi cuadrado es 0,008, que es menor que el valor crítico de 3,8415, lo que lleva a aceptar la h0. Esto indica que no existe una relación estadísticamente significativa entre el sexo y el consumo de tabaco en la muestra estudiada.

1. CHI CUADRADO
Paola Suárez Reina
Grupo 3. Subgrupo 14.

2. Elección de variables…
 Para usar el estadístico Chi Cuadrado, es necesario
estar comparando variables cualitativas.
 En este caso, las escogidas son tabaco y sexo.
 Es necesario establecer dos hipótesis
(suposiciones), para determinar la relación que
existe entre nuestras variables, estas pueden ser:
Hipótesis nula (H0): establece la igualdad entre
variables, y por lo tanto se debe al azar.
Hipótesis alternativa (H1): existe asociación entre
las variables, no son iguales. No es al azar, por lo
que existe una significación estadística.

3. Elección de variables…
 La forma de realizar este estudio será
teniendo en cuenta:
Las frecuencias observadas: las recogidas en los
datos.
Las frecuencias esperadas: las que se observan
si no existiera relación entre las dos variables. Es
decir si son independientes (se acepta H0).
 Fórmula de 𝑋2
𝑋2 = (𝑓𝑟𝑒𝑐𝑢𝑒𝑛𝑐𝑖𝑎𝑠 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑑𝑎𝑠 − 𝑓𝑟𝑒𝑐𝑢𝑒𝑛𝑐𝑖𝑎𝑠 𝑒𝑠𝑝𝑒𝑟𝑎𝑑𝑎𝑠)2 /𝑓𝑟𝑒𝑐𝑢𝑒𝑛𝑐𝑖𝑎𝑠 𝑒𝑠𝑝𝑒𝑟𝑎𝑑𝑎𝑠

4. Tabla de contingencia
 Ya escogidas las variables, las organizamos en
tablas de contingencia, que muestren una
mejor visualización de los datos, donde se
recogen las frecuencias observadas.
 H0: Tanto hombres como mujeres fuman lo
mismo.
 H1: Hombres y mujeres no fuman igual.
Sí fuman No fuman Total
Hombre 28 23 51
Mujer 135 103 238
Total 163 126 289

5. Frecuencias esperadas…
 Para llevar a cabo este cálculo se multiplican los
valores totales de cada categoría y se divide entre
el número total de casos (n).
𝐹𝐸1. 1= (23+28 )∗(23+103)/ 289 = 22,24
𝐹𝐸1. 2= (23+28 )∗ (28+135) /289 =28,76
𝐹𝐸2. 1= (103+135 )∗(23+103) /289 =103,76
𝐹𝐸2. 2= (103+135) ∗(28+135) /289 =134,24
 Estas serían las frecuencias que se obtendrían si
no existiera relación entre las variables, es decir, si
son independientes.

6. Frecuencias esperadas…
 Como los resultados obtenidos en el
cálculo de frecuencias esperadas es
bastante parecido al de las observadas,
se podría tomar H0 como cierta; sin
embargo, para confirmarlo es necesario
usar la fórmula de Chi Cuadrado.
𝑋 2 = (23−22.24) 2+(28−28,76) 2+(103−103,76)2+(135−134,24) 2
/22,24+27,76+103,76+134,24 =0,008022222
 Siendo este el valor de Chi Cuadrado teórica u
observada.

7. Decisión…
 Una vez calculada la Chi Cuadrado teórica hay
que, teniendo en cuenta el nivel de significación y
los grados de libertad, averiguar cuál es la
distribución teórica. Este valor teórico obtenido
fijará la zona de decisión, ya que dejará por debajo
un área de la curva de 0.05 .
 Según la distribución teórica, para un grado de
libertad y un nivel de significación de 0,05 la X2
=3,8415
 Como el valor 0,008 es menor que 3,8415, queda
dentro de la región de aceptación de H0. En
cambio si la rechazamos, tenemos una
probabilidad de equivocarnos mayor a 0,05 (que
era el valor máximo de error que estoy dispuesta

8. Tabla Chi Cuadrado

9. Conclusión…
 Aceptamos la H0, corroborando por tanto
que no existe relación entre nuestras
variables sexo y tabaco, sino que los
resultados se dan al azar.