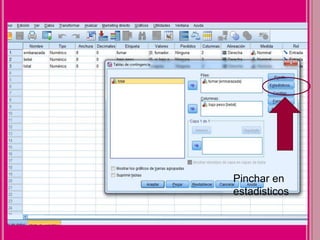
Este documento presenta dos problemas estadísticos que utilizan la prueba de chi cuadrado. El primer problema examina la relación entre el tabaquismo materno y el bajo peso al nacer. El segundo problema estudia la posible dependencia entre la práctica del tenis y la depresión. Ambos problemas siguen los mismos pasos de calcular las frecuencias esperadas, el estadístico chi cuadrado real y teórico, y compararlos para rechazar o no la hipótesis nula.
Directrices para la realización del informe de las prácticas de laboratorioJavier García Molleja
Guide for laboratory report made by students after laboratory sessions of Physics at Yachay Tech University (Urcuquí, Ecuador). Official guide during April-August 2017 semester.
Based on Ismael Mozo's work.
Pautas de Ayudantías (Introducción a la Microeconomía - UChile)Mauricio Vargas 帕夏
Ayudantías 1 a 9 (la totalidad de las ayudantías del curso)
Competencia perfecta, Monopolio, Teoría del consumidor, Teoría de la producción, Teoría de precios.
2. PROBLEMA 1: QUEREMOS VER LA RELACIÓN EXISTENTE EN UN
GRUPO DE EMBARAZADAS REFERENTE A SER FUMADORAS O NO
FUMADORAS Y QUE EL RN PRESENTE BAJO PESO AL NACER O NO LO
PRESENTE. TRABAJAR EN UN NIVEL DE CONFIANZA DEL 95%.
RECIEN NACIDO DE BAJO PESO
Gestante SI NO
Fumadora 43 (a) 207 (b) 43 + 207= 250
No Fumadora 105 (c) 1645 (d) 105 + 1645= 1750
43 + 105 =148 207 + 1645= 1852 N: 2000
A partir de los datos que se nos dan en la tabla que hace
referencia a las frecuencias observadas calculamos la
suma de las columnas que nos van a hacer falta a
continuación para calcular la frecuencia esperada.
3. La frecuencia esperada se calcula.
f(a) = (valor de la casilla de la suma de a + b) x valor de la casilla
a + c) / N = 18.5
f(b) = (valor de la casilla de la suma de a + b) x valor de la casilla
b + d) / N = 231.5
f(c) = (valor de la casilla de la suma de a + c) x valor de la casilla c
+ d) / N = 129.5
f(d) = (valor de la casilla de la suma de b + d) x valor de la casilla c
+ d) / N = 1620.5
18.5 231.5
129.5 1620.5
4. Tras esto, como ya conocemos la frecuencia observada y la
frecuencia esperada pues aplicamos la fórmula del chi cuadrado
que es la siguiente:
=
{ ( (43 – 18.5)2 / 18.5 ) + ( ( 207 – 231.5)2 / 231.5) + ( (105 – 129.5)2 /
129.5 ) + ( ( 1645 – 1620.5)2 / 1620.5) } = 40.04
Este valor obtenido hace referencia al chi cuadrado real pero para
saber si tenemos que aceptar o no la hipótesis nula necesitamos
calcular el valor teórico, el cual obtenemos través de las tablas; y
para ello necesitamos el nivel de confianza y los grados de libertad.
5. Como estamos trabajando con un nivel de confianza del 95 &
sabemos que es un 0,05
Y el grado de libertad al trabajar con mas de una variable se calcula :
(f – 1) x (c – 1), donde f hace referencia al numero de filas que en
este caso seria 2 y c al numero de columnas que en este caso
también seria 2, de manera que el grado de libertad es 1.
De esta manera buscaríamos en la tabla de chi cuadrado y
tendríamos que el valor teórico un nivel de confianza de 0,05 y 1
grado de libertad seria 3,84.
En dicho problema la Ho seria que no existe diferencia entre una mujer
embarazada fumadora o no fumadora y el peso que tenga el recién
nacido.
La H1 seria que si hay diferencia entre una mujer embarazada
fumadora y no fumadora y el peso del recién nacido.
Como chi cuadrado real es mayor que chi cuadrado teórico
rechazamos Ho .
6. Solución: Al ser el valor real mayor que el teórico rechazamos
hipótesis nula y aceptamos hipótesis alternativa lo que significa
que si hay diferencias entre las mujeres embarazadas fumadoras y
no fumadoras y el peso del recién nacido.
13. PROBLEMA 2: QUEREMOS ESTUDIAR LA POSIBLE DEPENDENCIA
ENTRE LA PRÁCTICA DE TENIS Y LA DEPRESIÓN, SE SELECCIONÓ UNA
MUESTRA ALEATORIA SIMPLE DE 100 JÓVENES, CON LOS SIGUIENTES
RESULTADOS: (TRABAJAR EN UN NIVEL DE CONFIANZA DEL 95%.)
SIN DEPRESION CON
DEPRESIÓN
PRACTICA
TENIS
38 (a) 9 (b) 47
NO PRACTICA
TENIS
31 (c) 22 (d) 53
69 31 N=100
Al igual que en el ejercicio anterior, partir de los datos que se nos
dan en la tabla que hace referencia a las frecuencias observadas
calculamos la suma de las columnas que nos van a hacer falta a
continuación para calcular la frecuencia esperada.
14. La frecuencia esperada se calcula.
f(a) = (valor de la casilla de la suma de a + b) x valor de la casilla a +
c) / N = 32.43
f(b) = (valor de la casilla de la suma de a + b) x valor de la casilla b +
d) / N = 14.57
f(c) = (valor de la casilla de la suma de a + c) x valor de la casilla c +
d) / N = 36.57
f(d) = (valor de la casilla de la suma de b + d) x valor de la casilla c +
d) / N = 16.43
32.43 14.57
36.57 16.43
15. Tras esto, como ya conocemos la frecuencia observada y la
frecuencia esperada pues aplicamos la fórmula del chi cuadrado
que es la siguiente:
{ ( (38 – 32.43)2 / 32.43 ) + ( ( 9 – 14.57)2 / 14.57) + ( (31 – 36.57)2 /
36.57 ) + ( ( 22 – 16.43)2 / 16.43) } = 5.87
Este valor obtenido hace referencia al chi cuadrado real pero para
saber si tenemos que aceptar o no la hipótesis nula necesitamos
calcular el valor teórico, el cual obtenemos través de las tablas; y para
ello necesitamos el nivel de confianza y los grados de libertad.
Como estamos trabajando con un nivel de confianza del 95 &
sabemos que es un 0,05
16. Y el grado de libertad al trabajar con mas de una variable se
calcula como en el ejercicio anterior: (f – 1) x (c – 1), donde
f hace referencia al numero de filas que en este caso seria 2
y c al numero de columnas que en este caso también seria 2,
de manera que el grado de libertad es 1.
De esta manera buscaríamos en la tabla de chi cuadrado y
tendríamos que el valor teórico un nivel de confianza de 0,05
y 1 grado de libertad seria 3,84.
En dicho problema la Ho seria que no existe dependencia entre
la práctica de tenis y la depresión.
La H1 seria que si hay dependencia entre la práctica de tenis y
la depresión.
Como chi cuadrado real es mayor que chi cuadrado teórico
rechazamos Ho .
17. Solución: Al ser el valor de chi cuadrado real mayor que el teórico
rechazamos hipótesis nula y aceptamos hipótesis alternativa lo
que significa que si hay dependencia entre la practica de tenis y la
depresión.
