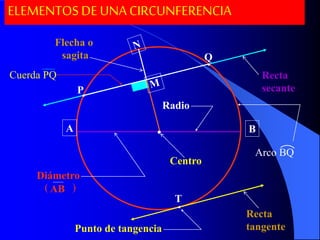
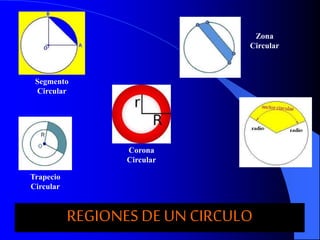
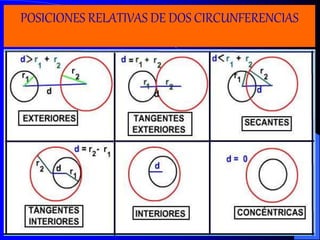
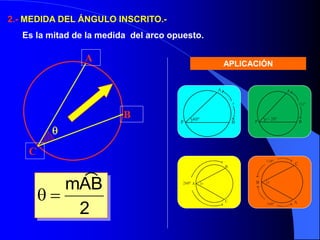
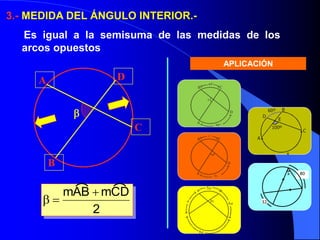
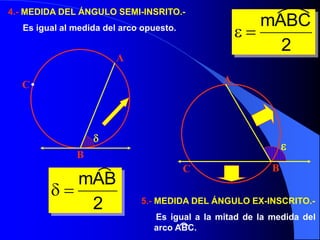
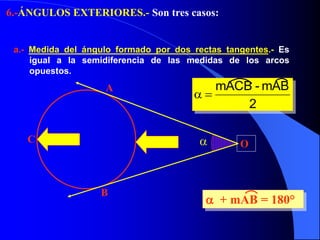
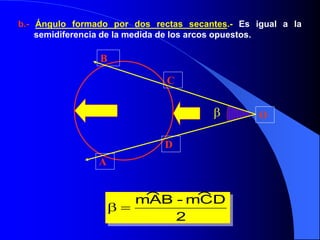
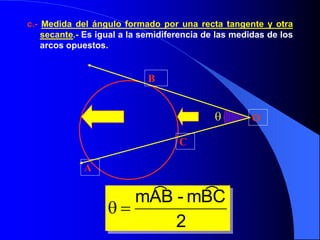
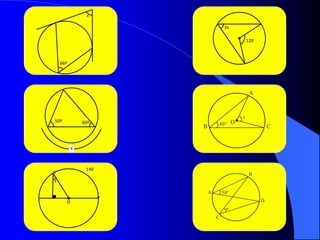
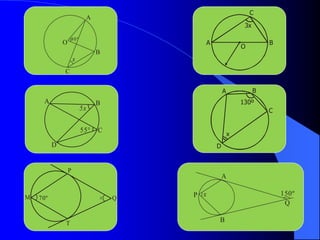
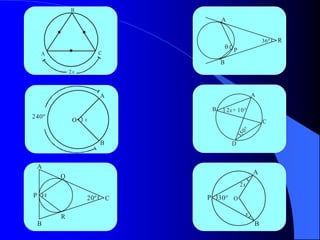
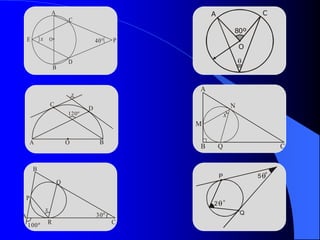
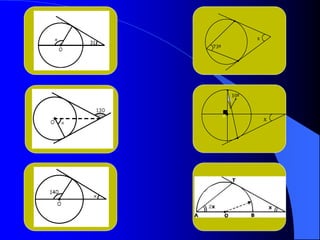
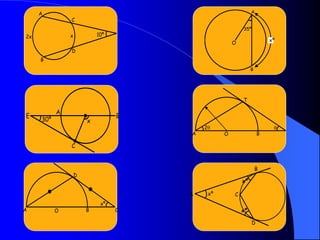
Este documento trata sobre la circunferencia y el círculo. Define una circunferencia como un conjunto de puntos equidistantes de un centro, y un círculo como la porción de plano dentro y sobre la circunferencia. Explica elementos como el diámetro, radio, arco y cuerda. Luego cubre temas como la medida de ángulos centrales, inscritos, interiores, semi-inscritos y exteriores, y cómo se relacionan con las medidas de arcos. Finalmente, presenta varios problemas para practicar est

1. CIRCUNFERENCIA
Y
CÍRCULO
Profesor :
Carlos E. Hernández Hernández
Grado:
2do de Secundaria
2014

2. CIRCUNFERENCIA
Es un lugar geométrico de un conjunto de infinitos
puntos que equidistan de un punto situado en el
centro.

3. CÍRCULO
Es la porción de plano que comprende la circunferencia
y su interior.
El perimetro del círculo es igual a la longitud de la
circunferencia, entonces se cumple:
Lo= 2πr

4. ELEMENTOS DE UNA CIRCUNFERENCIA
A B
Recta
secante
Recta
tangente
Flecha o
sagita
Diámetro
( A B )
Centro

T

Punto de tangencia
Q

P
Radio
Arco BQ
Cuerda PQ

5. Segmento
Circular
Zona
Circular
REGIONES DE UN CIRCULO
Trapecio
Circular
Corona
Circular

6. POSICIONES RELATIVAS DE DOS CIRCUNFERENCIAS

8. 1.- MEDIDA DEL ÁNGULO CENTRAL.-
Es igual a la medida del arco que se opone.

A
B
C
r
r
 = mAB
APLICACIÓN
O
A
2x 80º
B
O
A
x
2x-70º
B
O
5x

9. 2.- MEDIDA DEL ÁNGULO INSCRITO.-
Es la mitad de la medida del arco opuesto.

A
B
C
mAB
2
 
APLICACIÓN
A
x
40º
P B
A
132º
x+ 28º
P B
260º x
B x
B
A
C
C
A
120º
140º

10. 3.- MEDIDA DEL ÁNGULO INTERIOR.-
Es igual a la semisuma de las medidas de los
arcos opuestos

A
C
B
D
mAB mCD
2
 
APLICACIÓN
44º
B C
D
A
x
98º
B C
D
A
x
4x

5a
6a
8a
a
100º
A
C
B
D
60º
E
x
32
x 80

11. 4.- MEDIDA DEL ÁNGULO SEMI-INSRITO.-
Es igual al medida del arco opuesto.

A
B
C
mAB
2
 
mABC

A
C B
2
 
5.- MEDIDA DEL ÁNGULO EX-INSCRITO.-
Es igual a la mitad de la medida del
arco ABC.

12. 6.-ÁNGULOS EXTERIORES.- Son tres casos:
a.- Medida del ángulo formado por dos rectas tangentes.- Es
igual a la semidiferencia de las medidas de los arcos
opuestos.
mACB - mAB
 
C 
O
A
B
2
 + mAB = 180°

13. b.- Ángulo formado por dos rectas secantes.- Es igual a la
semidiferencia de la medida de los arcos opuestos.

B
A
C
O
D
mAB -mCD
2
 

14. c.- Medida del ángulo formado por una recta tangente y otra
secante.- Es igual a la semidiferencia de las medidas de los
arcos opuestos.

A
B
C
O
mAB - mBC
2
 

15. PROBLEMAS
VARIADOS

16. x
66º
50º 60º
x
x
O
140
3x
120
A
x
O
40º B C
C
B
D
A 50º


17. O
A
B
C
80°
x
A B
D
C
5x
55°
M 70º
x Q
P
T
C
3x
A B
O
A B
C
D
x
130º
150º
A
B
P
Q
x

18. B
A C
2x
x
A
B
240º
O
A
P C
B
Q
R
x
20º

36º
A
B
P
R
B 2x+ 10°
D
A
C
50 °
P
A
B
30° O
2x
x

19. A
. O
E 40° P
B
C
x
D
x
C
D
120º
A O B
30º
100º
x
A
B
C
P
Q
R
A C
80º
O

x
A
B
C
M
N
Q
Q
P
2
5°
°

20. 73º
x
10º
O x