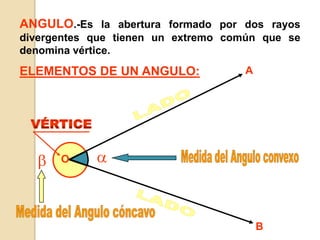
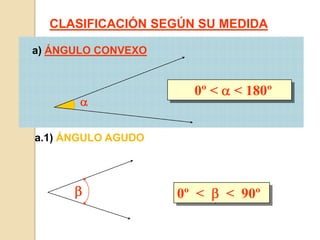
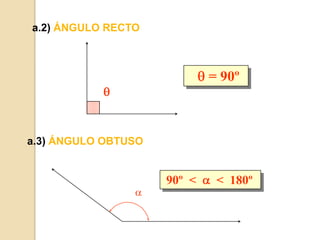
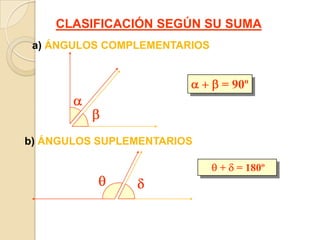
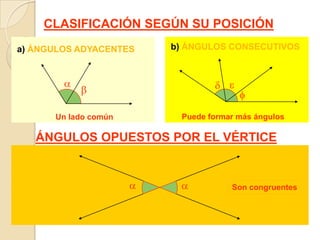
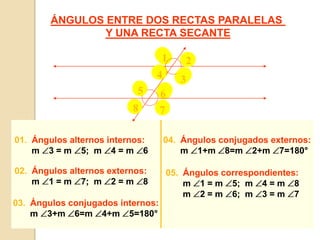
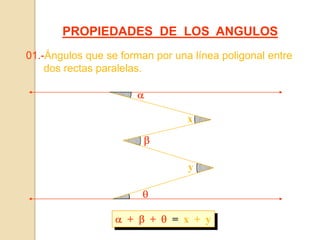
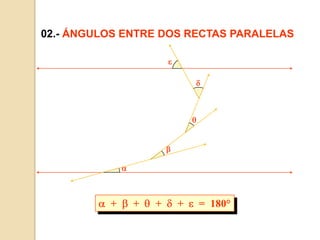
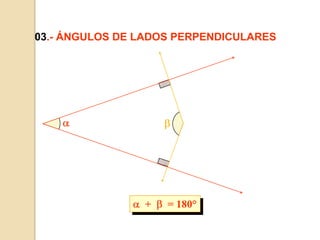
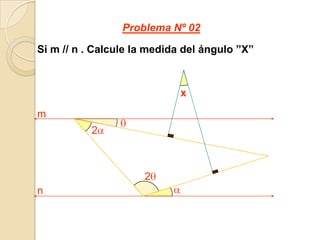
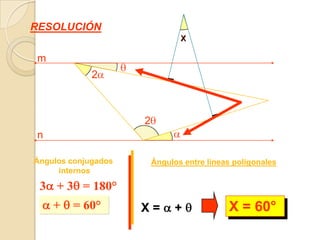
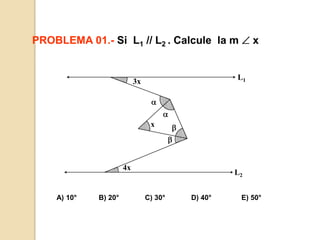
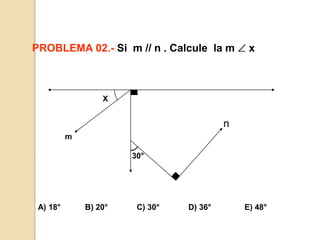
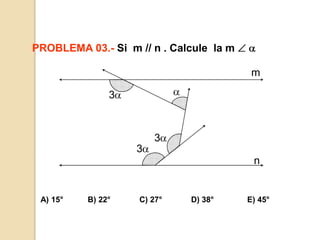
Este documento presenta información sobre ángulos. Define los elementos de un ángulo y clasifica los ángulos según su medida y posición. Explica las propiedades de los ángulos entre dos rectas paralelas y una recta secante. Incluye ejemplos de problemas resueltos y propuestos sobre ángulos entre paralelas.

1. I:E. “ VALLE SAGRADO” -URUBAMBAANGULOSTEORIA PROLEMAS RESUELTOS Y PROPUESTOSPROFESOR: ENRIQUE VELÁSQUEZ VALDIVIAE-MAIL: enrique.velasquez.valdivia@gmail.com

2. AVÉRTICELADOMedida del Angulo convexoOLADOMedida del Angulo cóncavoBANGULO.-Es la abertura formado por dos rayos divergentes que tienen un extremo común que se denomina vértice.ELEMENTOS DE UN ANGULO:

3. CLASIFICACIÓN SEGÚN SU MEDIDAa) ÁNGULO CONVEXO 0º <  < 180ºa.1) ÁNGULO AGUDO0º <  < 90º

4. a.2) ÁNGULO RECTO  = 90ºa.3) ÁNGULO OBTUSO 90º <  < 180º

5. CLASIFICACIÓN SEGÚN SU SUMAa) ÁNGULOS COMPLEMENTARIOS   = 90ºb) ÁNGULOS SUPLEMENTARIOS  +  = 180º

6. CLASIFICACIÓN SEGÚN SU POSICIÓNb) ÁNGULOS CONSECUTIVOSa) ÁNGULOS ADYACENTESPuede formar más ángulosUn lado comúnÁNGULOS OPUESTOS POR EL VÉRTICESon congruentes

7. 12435687ÁNGULOS ENTRE DOS RECTAS PARALELAS Y UNA RECTA SECANTE01. Ángulos alternos internos: m 3 = m 5; m 4 = m 604. Ángulos conjugados externos:m 1+m 8=m 2+m 7=180°02. Ángulos alternos externos:m 1 = m 7; m 2 = m 805. Ángulos correspondientes:m 1 = m 5; m 4 = m 8 m 2 = m 6; m 3 = m 703. Ángulos conjugados internos:m 3+m 6=m 4+m 5=180°

8. xyPROPIEDADES DE LOS ANGULOS01.-Ángulos que se forman por una línea poligonal entre dos rectas paralelas. +  +  = x + y

9. 02.- ÁNGULOS ENTRE DOS RECTAS PARALELAS +  +  +  +  = 180°

10. 03.- ÁNGULOS DE LADOS PERPENDICULARES +  = 180°

11. PROBLEMAS RESUELTOS

12. Problema Nº 01El complemento de la diferencia entre el suplemento y el complemento de un ángulo “X” es igual al duplo del complemento del ángulo “X”. Calcule la medida del ángulo “X”.RESOLUCIÓNLa estructura según el enunciado:90 - { ( ) - ( ) } = ( )290° - X180° - X90° - XDesarrollando se obtiene:90° - { 180° - X - 90° + X } = 180° - 2X90° - 90° = 180° - 2XLuego se reduce a:X = 90°2X = 180°

13. Si m // n . Calcule la medida del ángulo ”X”xm22nProblema Nº 02

14. xm22nRESOLUCIÓNxÁngulos conjugados internosÁngulos entre líneas poligonales3 + 3 = 180° +  = 60°X = 60°X =  + 

15. PROBLEMAS PROPUESTOSDE ANGULOSENTRE PARALELAS

16. L13xx4xL2PROBLEMA 01.- Si L1 // L2. Calcule la m  xA) 10° B) 20° C) 30° D) 40° E) 50°

17. Xnm30°PROBLEMA 02.-Si m // n . Calcule la m  xA) 18° B) 20° C) 30° D) 36° E) 48°

18. m333nPROBLEMA 03.-Si m // n . Calcule la m  A) 15° B) 22° C) 27° D) 38° E) 45°