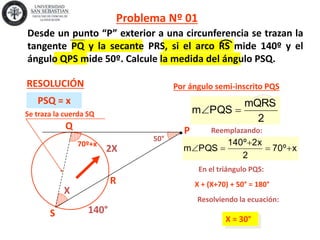
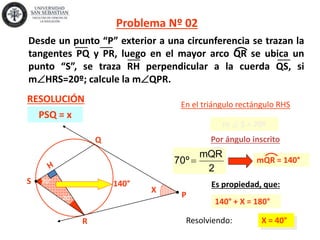
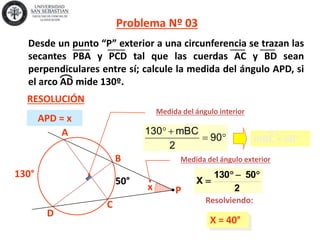
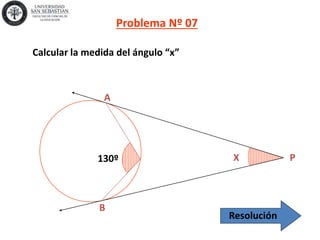
1) El documento presenta 10 problemas resueltos sobre geometría euclidiana que involucran ángulos, circunferencias y triángulos. 2) Los problemas se resuelven aplicando propiedades geométricas como el teorema de Poncelet y relaciones entre ángulos inscritos, exteriores y semi-inscritos. 3) Las soluciones incluyen ecuaciones y cálculos para determinar medidas de ángulos y lados de figuras.

2. 50°
70º+x
X
R
S
Q
140°
2X
X + (X+70) + 50° = 180°
X = 30°
Por ángulo semi-inscrito PQS
Problema Nº 01
RESOLUCIÓN
P
xº70
2
x2º140
PQSm 


Reemplazando:
En el triángulo PQS:
Resolviendo la ecuación:
PSQ = x
Se traza la cuerda SQ
2
mQRS
PQSm 
Desde un punto “P” exterior a una circunferencia se trazan la
tangente PQ y la secante PRS, si el arco RS mide 140º y el
ángulo QPS mide 50º. Calcule la medida del ángulo PSQ.

3. 20°
70°
X
X = 40°R
Q
En el triángulo rectángulo RHS
140° Es propiedad, que:
140° + X = 180°
Por ángulo inscrito
Problema Nº 02
RESOLUCIÓN
P
S
m  S = 70º
Resolviendo:
PSQ = x
2
mQR
º70  mQR = 140°
Desde un punto “P” exterior a una circunferencia se trazan la
tangentes PQ y PR, luego en el mayor arco QR se ubica un
punto “S”, se traza RH perpendicular a la cuerda QS, si
mHRS=20º; calcule la mQPR.

4. x
130°
A
C
B
D
X = 40°
2
50130
X

50°
Problema Nº 03
RESOLUCIÓN
P
Resolviendo:
APD = x
Medida del ángulo interior
Medida del ángulo exterior


90
2
mBC130
mBC = 50°
Desde un punto “P” exterior a una circunferencia se trazan las
secantes PBA y PCD tal que las cuerdas AC y BD sean
perpendiculares entre sí; calcule la medida del ángulo APD, si
el arco AD mide 130º.

5. Calcular la medida del ángulo “x”
Problema Nº 07
B
A
X P130º
Resolución

6. RESOLUCIÓN
B
A
X P130º C
Medida del ángulo inscrito:
En la circunferencia:
260º
Por la propiedad del ángulo exterior
formado por dos tangentes:
X = 80º
2
mAB
º130  mAB = 260º
mACB = 100º
mACB + x = 100º
260º + mACB = 360º

7. Calcule el perímetro del triángulo ABC.
Problema Nº 08
2
5 5
A
B
C
Resolución

8. Teorema de Poncelet: a + b = 10 + 2(2)
Luego el perímetro: (2p) = a + b + 10 = 14 + 10
(2p) = 24
RESOLUCIÓN
2
5 5
A
B
C
a b
a + b = 14 (1)
(2)
Reemplazando (1) en (2) (2p) = 14 + 10

9. X
PLANTEAMIENTO
Q
R
S
80º P
a
a
Problema Nº 09
Desde un punto “P” exterior a una circunferencia se
trazan la tangente PQ y la secante PRS de modo que los
arcos SQ y SR sean congruentes. Si el arco QR mide 80º,
calcular mQPR .
Resolución

10. 2a + 80º = 360º
a = 140º
Medida del ángulo exterior:
X
a



80
2
140 80
2
º º º
X = 30º
En la circunferencia:
RESOLUCIÓN
X
Q
R
S
80º P
a
a

11. P
Q
R
S
2
3
PLANTEAMIENTO
Problema Nº 10
En un cuadrilátero ABCD mQ = mS = 90º se traza la
diagonal PR. Los inradios de los triángulos PQR y PRS miden
3cm y 2cm respectivamente. Si el perímetro del cuadrilátero
PQRS es 22cm. Calcule la longitud de PR
Resolución

12. Teorema de Poncelet:
a b
c
d
PQR  a + b = PR+2(3) +
a +b + c + d = 2PR + 10
PR = 6cm
Dato:
a + b + c + d = 22cm
PSR  c + d = PR+2(2)
22 = 2PR + 10
RESOLUCIÓN
P
Q
R
S
2
3