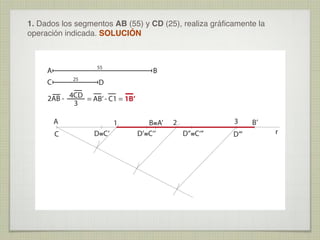
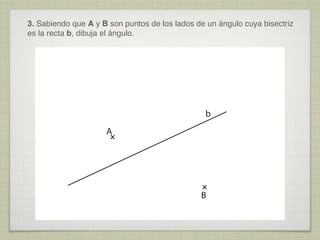
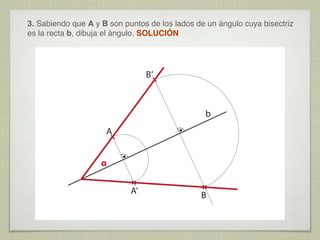
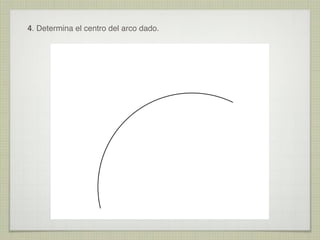
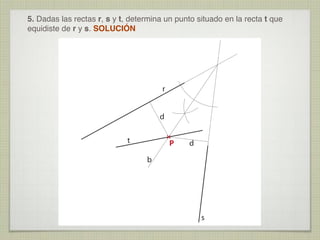
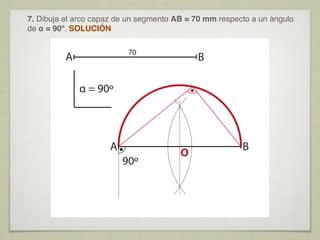
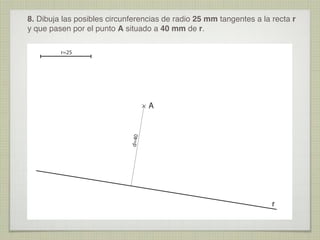
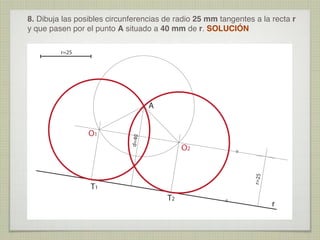
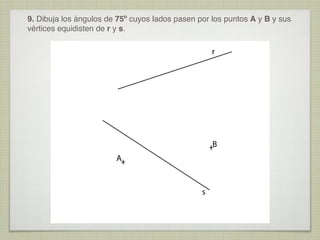
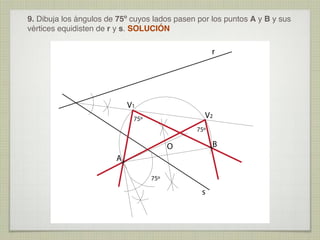
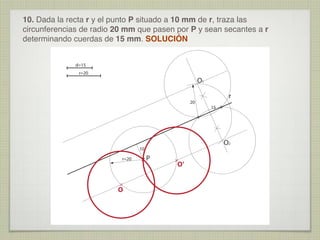
Este documento presenta 10 ejercicios de trazados geométricos fundamentales en el plano, con sus respectivas soluciones. Los ejercicios incluyen operaciones con segmentos y ángulos, determinación de centros, bisectrices, tangencias y secantes entre figuras geométricas como rectas, circunferencias y arcos.

1. EJERCICIOS DEL TEMA 1.
TRAZADOS FUNDAMENTALES EN EL PLANO
DIBUJO TÉCNICO 1º BACHILLERATO

2. 1. Dados los segmentos AB (55) y CD (25), realiza gráficamente la
operación indicada.
55
A
C
25
2AB - 4CD
3
D
B

3. 1. Dados los segmentos AB (55) y CD (25), realiza gráficamente la
operación indicada. SOLUCIÓN
55
A
25
C
B
D
2AB - 4CD = AB’ - C1 = 1B’
3
A
C
1
D≡C’
B≡A’
D’≡C‘’
3
2
D’’≡C‘’’
D’’’
B’
r

4. 2. Realiza gráficamente la operación de ángulos indicada sabiendo que α =
22º 30ʼ y β = 37º 30ʼ.
α+β
2

5. 2. Realiza gráficamente la operación de ángulos indicada sabiendo que α =
22º 30ʼ y β = 37º 30ʼ. SOLUCIÓN
α+β
2
α
β
22º 30’
α
β
37º 30’
α+β
2

6. 3. Sabiendo que A y B son puntos de los lados de un ángulo cuya bisectriz
es la recta b, dibuja el ángulo.
b
A
B

7. 3. Sabiendo que A y B son puntos de los lados de un ángulo cuya bisectriz
es la recta b, dibuja el ángulo. SOLUCIÓN
B’
b
A
α
A’
B

8. 4. Determina el centro del arco dado.

9. 4. Determina el centro del arco dado. SOLUCIÓN
C
B
A
O

10. 5. Dadas las rectas r, s y t, determina un punto situado en la recta t que
equidiste de r y s.
r
t
s

11. 5. Dadas las rectas r, s y t, determina un punto situado en la recta t que
equidiste de r y s. SOLUCIÓN
r
d
t
P
d
b
s

12. 6. Sabiendo que el ángulo β = 120º, dibuja un ángulo de α = 45º exterior a la
circunferencia O que pase por A y B.
B
O
A
β=120º

13. 6. Sabiendo que el ángulo β = 120º, dibuja un ángulo de α = 45º exterior a la
circunferencia O que pase por A y B. SOLUCIÓN
V
α=45º
D
C
B
γ=30º
O
A
β=120º
β-γ
α=
2
120º-γ
45º=
2
γ=30º

14. 7. Dibuja el arco capaz de un segmento AB = 70 mm respecto a un ángulo
de α = 90º.
70
A
α = 90º
B

15. 7. Dibuja el arco capaz de un segmento AB = 70 mm respecto a un ángulo
de α = 90º. SOLUCIÓN
70
A
B
α = 90º
A
90º
O
B

16. 8. Dibuja las posibles circunferencias de radio 25 mm tangentes a la recta r
y que pasen por el punto A situado a 40 mm de r.
r=25
d=40
A
r

17. 8. Dibuja las posibles circunferencias de radio 25 mm tangentes a la recta r
y que pasen por el punto A situado a 40 mm de r. SOLUCIÓN
r=25
O2
r=25
=
O1
d=40
A
T2
=
T1
r

18. 9. Dibuja los ángulos de 75º cuyos lados pasen por los puntos A y B y sus
vértices equidisten de r y s.
r
B
A
s

19. 9. Dibuja los ángulos de 75º cuyos lados pasen por los puntos A y B y sus
vértices equidisten de r y s. SOLUCIÓN
r
V1
V2
75º
75º
B
O
A
75º
s

20. 10. Dada la recta r y el punto P situado a 10 mm de r, traza las
circunferencias de radio 20 mm que pasen por P y sean secantes a r
determinando cuerdas de 15 mm.
d=15
r=20
r
10
P

21. 10. Dada la recta r y el punto P situado a 10 mm de r, traza las
circunferencias de radio 20 mm que pasen por P y sean secantes a r
determinando cuerdas de 15 mm. SOLUCIÓN
d=15
r=20
O1
20
O
15
O2
10
r=20
r
P
O’

22. F, MOHEDANO
DIBUJO TÉCNICO 1º BACH.
IES LOS MANANTIALES (TORREMOLINOS)