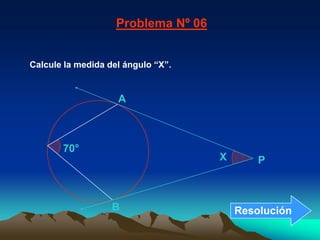
El documento describe los elementos básicos de una circunferencia y las propiedades de los ángulos asociados a ella. Explica que la medida de un ángulo central es igual a la medida del arco opuesto, la medida de un ángulo interior es igual a la semisuma de los arcos opuestos, y la medida de un ángulo inscrito es la mitad del arco opuesto. También resuelve problemas aplicando estas propiedades para calcular medidas de ángulos desconocidos.

1. CIRCUNFERENCIA

2. Flecha o sagitaNQCuerda PQRectasecanteMPRadioABArco BQCentroDiámetro( )ABTRectatangentePunto de tangenciaELEMENTOS DE UNA CIRCUNFERENCIA

3. ANGULOSEN LACIRCUNFERENCIA

4. ArCrB = mAB1.- MEDIDA DEL ÁNGULO CENTRAL.- Es igual a la medida del arco que se opone.

5. DACB2.- MEDIDA DEL ÁNGULO INTERIOR.- Es igual a la semisuma de las medidas de los arcos opuestos

6. ABC3.- MEDIDA DEL ÁNGULO INSCRITO.- Es la mitad de la medida del arco opuesto.

7. ACB4.- MEDIDA DEL ÁNGULO SEMI-INSRITO.- Es igual al medida del arco opuesto.

8. 1.- MEDIDA DEL ÁNGULO EX-INSCRITO.- Es igual a la mitad de la medida del arco ABC. ABC

9. ACOB + mAB = 180°6.-ÁNGULOS EXTERIORES.- Son tres casos:a.- Medida del ángulo formado por dos rectas tangentes.- Es igual a la semidiferencia de las medidas de los arcos opuestos.

10. BCODAb.-Ángulo formado por dos rectas secantes.- Es igual a la semidiferencia de la medida de los arcos opuestos.

11. BOCAc.- Medida del ángulo formado por una recta tangente y otra secante.- Es igual a la semidiferencia de las medidas de los arcos opuestos.

12. PROBLEMASRESUELTOS

13. Desde un punto “P” exterior a una circunferencia se trazan la tangente PQ y la secante PRS, si el arco RS mide 140º y el ángulo QPS mide 50º. Calcule la medida del ángulo PSQ.Se traza la cuerda SQQP50°70º+xRXSProblema Nº 01RESOLUCIÓNPor ángulo semi-inscrito PQS PSQ = xReemplazando:2XEn el triángulo PQS:X + (X+70) + 50° = 180°Resolviendo la ecuación:140°X = 30°

14. A70°XPBResoluciónProblema Nº 06Calcule la medida del ángulo “X”.

15. CAmAB=140º70°XPBRESOLUCIÓN140ºMedida del ángulo inscrito:Por la propiedad del ángulo exterior formado por dos tangentes: X = 40º Resolviendo:140º + x = 180º

16. APX130ºBResoluciónProblema Nº 07Calcular la medida del ángulo “x”

17. CAPX130ºmAB = 260ºmACB = 100º260º + mACB = 360º BmACB + x = 100ºRESOLUCIÓN260ºMedida del ángulo inscrito:En la circunferencia:Por la propiedad del ángulo exterior formado por dos tangentes:X = 80º