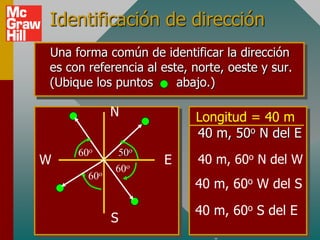
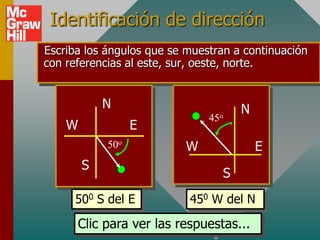
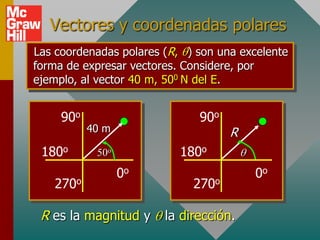
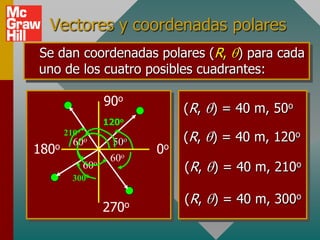
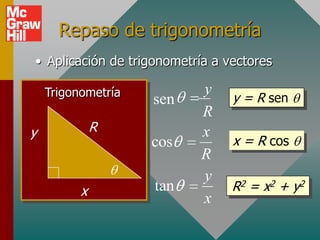
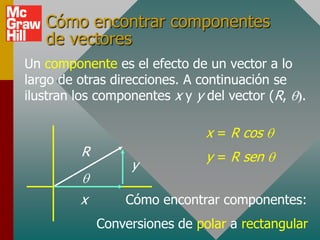
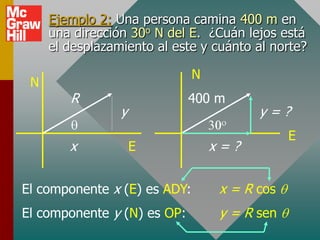
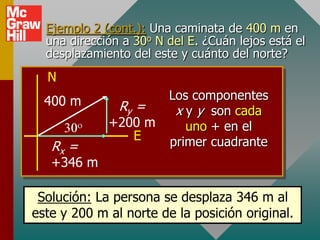
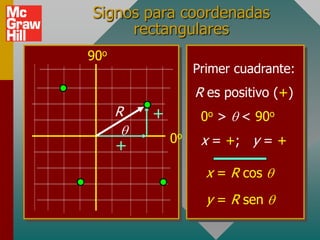
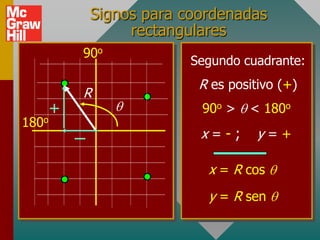
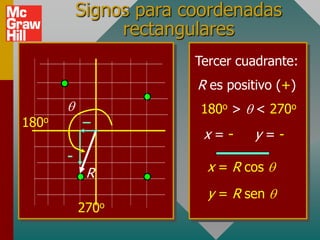
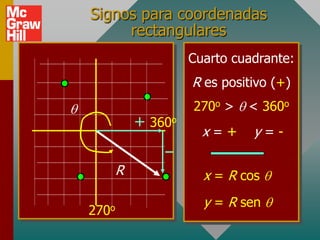
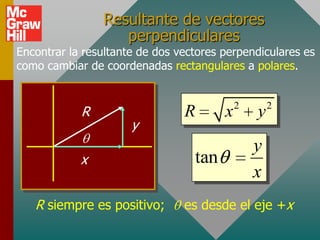
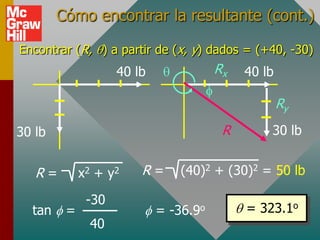
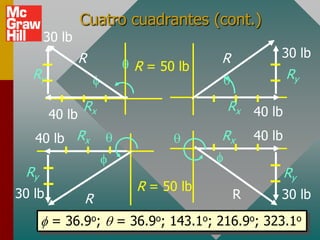
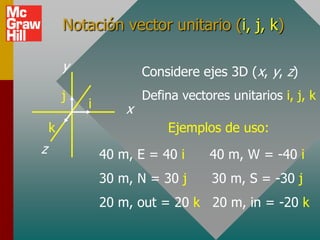
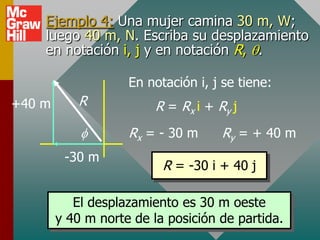
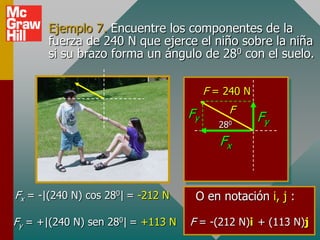
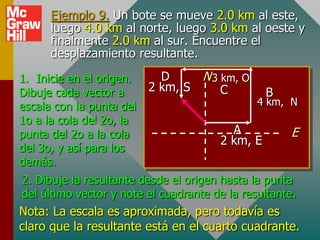
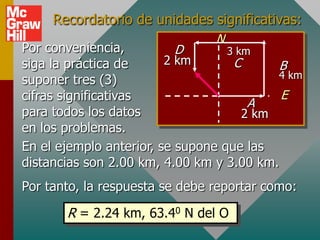
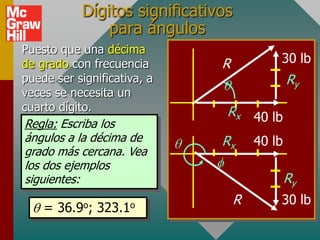
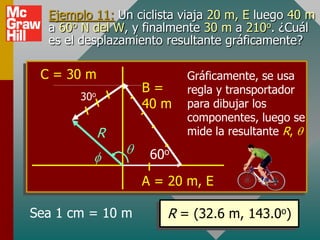
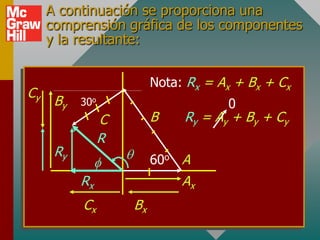
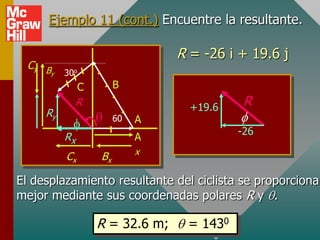
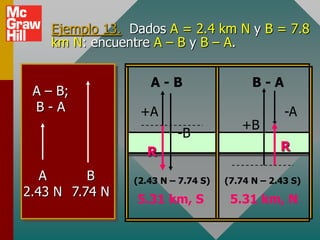
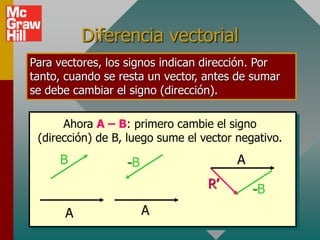
Este documento presenta los conceptos básicos de vectores. Explica que un vector contiene magnitud y dirección, mientras que una cantidad escalar solo contiene magnitud. Describe cómo encontrar los componentes de un vector a lo largo de los ejes x e y, y cómo determinar la resultante de dos o más vectores mediante la suma de sus componentes correspondientes. También cubre la notación de coordenadas polares y rectangulares para expresar vectores, así como el uso de la trigonometría para resolver problemas de vectores.

1. Vectores
Presentación PowerPoint de
Paul E. Tippens, Profesor de Física
Southern Polytechnic State University

2. Vectores
Los topógrafos usan mediciones precisas
de magnitudes y direcciones para crear
mapas a escala de grandes regiones.

3. Objetivos: Después de completar
este módulo, deberá:
• Demostrar que cumple las expectativas matemáticas:
análisis de unidades, álgebra, notación científica y
trigonometría de triángulo recto.
• Definir y dar ejemplos de cantidades escalares y
vectoriales.
• Determinar los componentes de un vector dado.
• Encontrar la resultante de dos o más vectores.

4. Expectativas
• Debe ser capaz de convertir unidades
de medición para cantidades físicas.
Convierta 40 m/s en kilómetros por hora.
m 1 km 3600 s
40--- x ---------- x -------- = 144 km/h
s 1000 m 1h

5. Expectativas (cont.):
• Se supone manejo de álgebra
universitaria y fórmulas simples.
v0 vf
Ejemplo: x t Resuelva para vo
2
v f t 2x
v0
t

6. Expectativas (cont.)
• Debe ser capaz de trabajar en notación
científica.
Evalúe lo siguiente:
Gmm’ (6.67 x 10-11)(4 x 10-3)(2)
F = -------- = ------------
r 2 (8.77 x 10-3)2
F = 6.94 x 10-9 N = 6.94 nN

7. Expectativas (cont.)
• Debe estar familiarizado con prefijos del SI
metro (m) 1 m = 1 x 100 m
1 Gm = 1 x 109 m 1 nm = 1 x 10-9 m
1 Mm = 1 x 106 m 1 m = 1 x 10-6 m
1 km = 1 x 103 m 1 mm = 1 x 10-3 m

8. Expectativas (cont.)
• Debe dominar la trigonometría del
triángulo recto.
y y = R sen
sen
R
y R
x
cos x = R cos
R
y 2
x tan R = x2 + y 2
x

9. Repaso de matemáticas
Si siente necesidad de
pulir sus habilidades
matemáticas, intente el
tutorial del Capítulo 2
acerca de matemáticas.
La trigonometría se
revisa junto con los
vectores en este módulo.
Seleccione Capítulo 2 del On-Line Learning
Center en Tippens-Student Edition

10. La física es la ciencia
de la medición
Longitud Peso Tiempo
Comience con la medición de longitud:
su magnitud y su dirección.

11. Distancia: cantidad escalar
 Distancia es la longitud de la ruta
tomada por un objeto.
Una cantidad escalar:
s = 20 m B
Sólo contiene magnitud
y consiste de un
A
número y una unidad.
(20 m, 40 mi/h, 10 gal)

12. Desplazamiento-Cantidad vectorial
• Desplazamiento es la separación en
línea recta de dos puntos en una
dirección especificada.
Una cantidad vectorial:
D = 12 m, 20o B
Contiene magnitud Y
A dirección, un número,
unidad y ángulo.
(12 m, 300; 8 km/h, N)

13. Distancia y desplazamiento
• Desplazamiento es la coordenada x o y
de la posición. Considere un auto que
viaja 4 m E, luego 6 m W.
Desplazamiento neto:
D 4 m, E D = 2 m, W
¿Cuál es la distancia
x = -2 x = +4 recorrida?
6 m, W ¡¡ 10 m !!

14. Identificación de dirección
Una forma común de identificar la dirección
es con referencia al este, norte, oeste y sur.
(Ubique los puntos abajo.)
N Longitud = 40 m
40 m, 50o N del E
60o 50o
W E 40 m, 60o N del W
60o
60o
40 m, 60o W del S
40 m, 60o S del E
S

15. Identificación de dirección
Escriba los ángulos que se muestran a continuación
con referencias al este, sur, oeste, norte.
N N
45o
W E
50o W E
S
S
500 S del E 450 W del N
Clic para ver las respuestas...

16. Vectores y coordenadas polares
Las coordenadas polares (R, ) son una excelente
forma de expresar vectores. Considere, por
ejemplo, al vector 40 m, 500 N del E.
90o 90o
40 m R
180o 50o 180o
0o 0o
270o 270o
R es la magnitud y la dirección.

17. Vectores y coordenadas polares
Se dan coordenadas polares (R, ) para cada
uno de los cuatro posibles cuadrantes:
90o
(R, ) = 40 m, 50o
120o
210o
60o 50o (R, ) = 40 m, 120o
180o 0o
60o
60o (R, ) = 40 m, 210o
3000
(R, ) = 40 m, 300o
270o

18. Coordenadas rectangulares
y La referencia se hace
(-2, +3) a los ejes x y y,
(+3, +2) y los números + y –
+ indican posición en
+ el espacio.
x
- Derecha, arriba = (+, +)
- Izquierda, abajo = (-, -)
(x, y) = (?, ?)
(-1, -3) (+4, -3)

19. Repaso de trigonometría
• Aplicación de trigonometría a vectores
Trigonometría y
sen y = R sen
R
y R x
cos x = R cos
R
y
x tan R2 = x2 + y2
x

20. Ejemplo 1: Encuentre la altura de un
edificio si proyecta una sombra de 90 m
de largo y el ángulo indicado es de 30o.
La altura h es opuesta a 300 y el lado
adyacente conocido es de 90 m.
op h
tan 30
ady 90 m
h
300
h = (90 m) tan 30o
90 m
h = 57.7 m

21. Cómo encontrar componentes
de vectores
Un componente es el efecto de un vector a lo
largo de otras direcciones. A continuación se
ilustran los componentes x y y del vector (R, .
x = R cos
R y = R sen
y
x Cómo encontrar componentes:
Conversiones de polar a rectangular

22. Ejemplo 2: Una persona camina 400 m en
una dirección 30o N del E. ¿Cuán lejos está
el desplazamiento al este y cuánto al norte?
N
N
R 400 m
y y=?
E
x E x=?
El componente x (E) es ADY: x = R cos
El componente y (N) es OP: y = R sen

23. Ejemplo 2 (cont.): Una caminata de 400 m en
una dirección a 30o N del E. ¿Cuán lejos está el
desplazamiento del este y cuánto del norte?
N Nota: x es el lado
400 m adyacente al ángulo de 300
y=?
E ADY = HIP x cos 300
x=?
x = R cos
x = (400 m) cos 30o El componente x es:
= +346 m, E Rx = +346 m

24. Ejemplo 2 (cont.): Una caminata de 400 m en
una dirección a 30o N del E. ¿Cuán lejos está
el desplazamiento del este y cuánto del norte?
N Nota: y es el lado opuesto
400 m al ángulo de 300
y=?
E OP = HIP x sen 300
x=?
y = R sen
y = (400 m) sen 30o El componente y es:
= + 200 m, N Ry = +200 m

25. Ejemplo 2 (cont.): Una caminata de 400 m en
una dirección a 30o N del E. ¿Cuán lejos está el
desplazamiento del este y cuánto del norte?
N
400 m Los componentes
Ry = x y y son cada
+200 m uno + en el
E primer cuadrante
Rx =
+346 m
Solución: La persona se desplaza 346 m al
este y 200 m al norte de la posición original.

26. Signos para coordenadas
rectangulares
90o
Primer cuadrante:
R es positivo (+)
R + 0o > < 90o
0o x = +; y = +
+
x = R cos
y = R sen

27. Signos para coordenadas
rectangulares
90o
Segundo cuadrante:
R es positivo (+)
R
+ 90o > < 180o
180o
x=-; y=+
x = R cos
y = R sen

28. Signos para coordenadas
rectangulares
Tercer cuadrante:
R es positivo (+)
180o > < 270o
180o
x=- y=-
-
R x = R cos
y = R sen
270o

29. Signos para coordenadas
rectangulares
Cuarto cuadrante:
R es positivo (+)
270o > < 360o
+ 360o
x=+ y=-
R x = R cos
y = R sen
270o

30. Resultante de vectores
perpendiculares
Encontrar la resultante de dos vectores perpendiculares es
como cambiar de coordenadas rectangulares a polares.
2 2
R R x y
y
y
x tan
x
R siempre es positivo; es desde el eje +x

31. Ejemplo 3: Una fuerza de 30 lb hacia el sur y
una de 40 lb hacia el este actúan sobre un
burro al mismo tiempo. ¿Cuál es la fuerza
NETA o resultante sobre el burro?
Dibuje un esquema burdo. Elija una escala burda:
Ej: 1 cm = 10 lb
40 lb 40 lb
Nota: La fuerza tiene direccióncm = 40 lb
4 tal como la
longitud. Los vectores fuerza se pueden tratar
como si se tuvieran vectores 3 cm = 30 lb
30 lb longitud para
30 lb
encontrar la fuerza resultante. ¡El

32. Cómo encontrar la resultante (cont.)
Encontrar (R, ) a partir de (x, y) dados = (+40, -30)
40 lb Rx 40 lb
Ry
30 lb R 30 lb
R= x2 + y 2 R= (40)2 + (30)2 = 50 lb
-30
tan = = -36.9o = 323.1o
40

33. Cuatro cuadrantes (cont.)
30 lb
R R 30 lb
R = 50 lb
Ry Ry
Rx Rx 40 lb
40 lb
40 lb Rx Rx 40 lb
Ry Ry
R = 50 lb
30 lb R R 30 lb
= 36.9o; = 36.9o; 143.1o; 216.9o; 323.1o

34. Notación vector unitario (i, j, k)
y Considere ejes 3D (x, y, z)
j Defina vectores unitarios i, j, k
i x
k Ejemplos de uso:
z 40 m, E = 40 i 40 m, W = -40 i
30 m, N = 30 j 30 m, S = -30 j
20 m, out = 20 k 20 m, in = -20 k

35. Ejemplo 4: Una mujer camina 30 m, W;
luego 40 m, N. Escriba su desplazamiento
en notación i, j y en notación R, .
En notación i, j se tiene:
+40 m R R = Rx i + Ry j
Rx = - 30 m Ry = + 40 m
-30 m
R = -30 i + 40 j
El desplazamiento es 30 m oeste
y 40 m norte de la posición de partida.

36. Ejemplo 4 (cont.): A continuación se
encuentra su desplazamiento en
notación R, .
40
tan ; = 59.10
+40 R 30
m
= 1800 – 59.10
-30 m
= 126.9o
R ( 30) 2
(40) 2
R = 50 m
(R, ) = (50 m, 126.9o)

37. Ejemplo 6: La ciudad A está 35 km al sur y
46 km al oeste de la ciudad B. Encuentre la
longitud y dirección de la autopista entre las
ciudades.
46 km
R = -46 i – 35 j
R (46 km)2 (35 km)2 35 B
km
R = 57.8 km R=?
A
46 km
tan
35 km = 1800 + 52.70
= 52.70 S de W. = 232.70

38. Ejemplo 7. Encuentre los componentes de la
fuerza de 240 N que ejerce el niño sobre la niña
si su brazo forma un ángulo de 280 con el suelo.
F = 240 N
Fy F
280
Fy
Fx
Fx = -|(240 N) cos 280| = -212 N O en notación i, j :
Fy = +|(240 N) sen 280| = +113 N F = -(212 N)i + (113 N)j

39. Ejemplo 8. Encuentre los componentes de
una fuerza de 300 N que actúa a lo largo del
manubrio de una podadora. El ángulo con el
suelo es de 320.
F = 300 N
32o
Fx
32o 320
Fy F Fy
Fx = -|(300 N) cos 320| = -254 N O en notación i, j
:
Fy = -|(300 N) sen 320| = -159 N F = -(254 N)i - (159 N)j

40. Método de componentes
1. Inicie en el origen. Dibuje cada vector a escala
con la punta del 1o a la cola del 2o, la punta del
2o a la cola del 3o, y así para los demás.
2. Dibuje la resultante desde el origen hasta la
punta del último vector y note el cuadrante de la
resultante.
3. Escriba cada vector en notación i, j.
4. Sume algebraicamente los vectores para obtener
la resultante en notación i, j. Luego convierta a
(R, ).

41. Ejemplo 9. Un bote se mueve 2.0 km al este,
luego 4.0 km al norte, luego 3.0 km al oeste y
finalmente 2.0 km al sur. Encuentre el
desplazamiento resultante.
1. Inicie en el origen. D N 3 km, O
Dibuje cada vector a 2 km, S C B
escala con la punta del 4 km, N
1o a la cola del 2o, la
punta del 2o a la cola A E
2 km, E
del 3o, y así para los
demás.
2. Dibuje la resultante desde el origen hasta la punta
del último vector y note el cuadrante de la resultante.
Nota: La escala es aproximada, pero todavía es
claro que la resultante está en el cuarto cuadrante.

42. Ejemplo 9 (cont.) Encuentre el
desplazamiento resultante.
3. Escriba cada vector N
D 3 km, O
en notación i, j: 2 km, S C B
A = +2 i 4 km, N
B= +4j E
A
C = -3 i 2 km, E
D= -2j 4. Sume algebraicamente
los vectores A, B, C, D
R = -1 i + 2 j para obtener la resultante
en notación i, j.
1 km al oeste y 2 km 5. Convierta a notación R,
al norte del origen. Vea página siguiente.

43. Ejemplo 9 (cont.) Encuentre desplazamiento
resultante.
N
La suma resultante es: D 3 km, O
2 km, S C B
R = -1 i + 2 j 4 km, N
Ahora encuentre R,
E
R ( 1) 2
(2) 2
5 A
2 km, E
R = 2.24 km
tan
2 km R Ry = +2
1 km km
= 63.40 N del O Rx = -1 km

44. Recordatorio de unidades significativas:
N
Por conveniencia, D 3 km
siga la práctica de 2 km C B
4 km
suponer tres (3)
cifras significativas E
A
para todos los datos 2 km
en los problemas.
En el ejemplo anterior, se supone que las
distancias son 2.00 km, 4.00 km y 3.00 km.
Por tanto, la respuesta se debe reportar como:
R = 2.24 km, 63.40 N del O

45. Dígitos significativos
para ángulos
Puesto que una décima
de grado con frecuencia R 30 lb
puede ser significativa, a Ry
veces se necesita un
cuarto dígito. Rx 40 lb
Regla: Escriba los
ángulos a la décima de Rx 40 lb
grado más cercana. Vea
los dos ejemplos
siguientes: Ry
R 30 lb
= 36.9o; 323.1o

46. Ejemplo 10: Encontrar R, para los tres
desplazamientos vectoriales siguientes:
A = 5 m, 00 C=
R 0.5 m
B = 2.1 m, 200 B
200
C = 0.5 m, 900
A=5m B = 2.1 m
1. Primero dibuje los vectores A, B y C a escala
aproximada y los ángulos indicados. (Dibujo burdo)
2. Dibuje la resultante desde el origen hasta la punta
del último vector; note el cuadrante de la
resultante. (R, )
3. Escriba cada vector en notación i, j. (continúa...)

47. Ejemplo 10: Encuentre R, para los tres
desplazamientos vectoriales siguientes. (Puede
ser útil una tabla.)
Para notación i, j, C=
encuentre los R 0.5 m
componentes x, y B
200
de cada vector A,
B, C. A=5m B = 2.1 m
Vector componente x (i) componente y (j)
A=5m 00 +5m 0
B = 2.1 m 200 +(2.1 m) cos 200 +(2.1 m) sen 200
C = 0.5 m 900 0 + 0.5 m
Rx = Ax + Bx + Cx Ry = Ay + By + Cy

48. Ejemplo 10 (cont.): Encuentre i, j para
tres vectores: A = 5 m, 00; B = 2.1 m,
200; C = 0.5 m, 900.
componente x (i) componente y (j)
Ax = + 5.00 m Ay = 0
Bx = +1.97 m By = +0.718 m
Cx = 0 Cy = + 0.50 m
4. Sume los vectores A = 5.00 i + 0j
para obtener la B = 1.97 i + 0.718 j
resultante R en
C= 0 i + 0.50 j
notación i, j.
R = 6.97 i + 1.22 j

49. Ejemplo 10 (cont.): Encuentre i, j para tres
vectores: A = 5 m, 00; B = 2.1 m, 200; C = 0.5
m, 900.
R = 6.97 i + 1.22 j Diagrama para
encontrar R,
5. Determine R, a partir
de x, y: R Ry
R (6.97 m)2 (1.22 m) 2 1.22 m
Rx= 6.97 m
R = 7.08 m
1.22 m
tan = 9.930 N del E
6.97 m

50. Ejemplo 11: Un ciclista viaja 20 m, E luego 40 m
a 60o N del W, y finalmente 30 m a 210o. ¿Cuál
es el desplazamiento resultante gráficamente?
C = 30 m Gráficamente, se usa
B= regla y transportador
30o
40 m para dibujar los
componentes, luego se
R mide la resultante R,
60o
A = 20 m, E
Sea 1 cm = 10 m R = (32.6 m, 143.0o)

51. A continuación se proporciona una
comprensión gráfica de los componentes
y la resultante:
Nota: Rx = Ax + Bx + Cx
Cy
By 30o 0
C B Ry = Ay + By + Cy
R
Ry
60o A
Rx Ax
Cx Bx

52. Ejemplo 11 (cont.) Use el método de
componentes para encontrar la resultante.
Escriba cada vector
Cy B en notación i, j.
y 30o
C B Ax = 20 m, Ay = 0
R
Ry A = 20 i
60 A
Rx A
Bx = -40 cos 60o = -20 m
Cx Bx x By = 40 sen 60o = +34.6 m
B = -20 i + 34.6 j
Cx = -30 cos 30o = -26 m
Cy = -30 sen 60o = -15 m C = -26 i - 15 j

53. Ejemplo 11 (cont.) Método de componentes
Sume algebraicamente:
Cy B
y 30o
A = 20 i
C B
B = -20 i + 34.6 j
R
Ry 60 A C = -26 i - 15 j
Rx A R = -26 i + 19.6 j
x
Cx Bx
R= (-26)2 + (19.6)2 = 32.6 m
+19.6 R
19.6
tan = = 143o
-26 -26

54. Ejemplo 11 (cont.) Encuentre la resultante.
R = -26 i + 19.6 j
Cy B
y 30o
C B
R +19.6 R
Ry 60 A
-26
Rx A
x
Cx Bx
El desplazamiento resultante del ciclista se proporciona
mejor mediante sus coordenadas polares R y .
R = 32.6 m; = 1430

55. Ejemplo 12. Encuentre A + B + C para los
vectores que se muestran a continuación.
B Cx
A = 5 m, 900
A Cy
B = 12 m, 00
C
C = 20 m, -350
R
Ax = 0; Ay = +5 m
A= 0 i + 5.00 j
Bx = +12 m; By = 0 B = 12 i + 0j
Cx = (20 m) cos 350 C = 16.4 i – 11.5 j
Cy = -(20 m) sen -350 R = 28.4 i - 6.47 j

56. Ejemplo 12 (cont.). Encuentre A + B + C
B Rx = 28.4 m
A
C R
R Ry = -6.47 m
R = 29.1 m
2 2
R (28.4 m) (6.47 m)
6.47 m
tan = 12.80 S del E
28.4 m

57. Diferencia vectorial
Para vectores, los signos indican la dirección. Por
tanto, cuando se resta un vector, antes de sumar
se debe cambiar el signo (dirección).
Considere primero A + B gráficamente:
R=A+B
B
R
B
A A

58. Diferencia vectorial
Para vectores, los signos indican la dirección. Por
tanto, cuando se resta un vector, antes de sumar
se debe cambiar el signo (dirección).
Ahora A – B: primero cambie el signo
(dirección) de B, luego sume el vector negativo.
B -B A
R’ -B
A A

59. Suma y resta
La resta resulta en un diferencia significativa tanto
en la magnitud como en la dirección del vector
resultante. |(A – B)| = |A| - |B|
Comparación de suma y resta de B
R=A+B R’ = A - B
B
A
R
B R’ -B
A A

60. Ejemplo 13. Dados A = 2.4 km N y B = 7.8
km N: encuentre A – B y B – A.
A-B B-A
A – B;
B-A +A -A
+B
-B
R R
A B (2.43 N – 7.74 S) (7.74 N – 2.43 S)
2.43 N 7.74 N
5.31 km, S 5.31 km, N

61. Resumen para vectores
 Una cantidad escalar se especifica completamente
sólo mediante su magnitud. (40 m, 10 gal)
 Una cantidad vectorial se especifica completamente
mediante su magnitud y dirección. (40 m, 300)
Componentes de R:
R
Ry
Rx = R cos
Ry = R sen Rx

62. Continúa resumen:
 Encontrar la resultante de dos vectores
perpendiculares es como convertir de coordenadas
polares (R, ) a rectangulares (Rx, Ry).
Resultante de vectores:
R
R x 2
y 2
Ry
y
tan Rx
x

63. Método de componentes
para vectores
 Inicie en el origen y dibuje cada vector en
sucesión para formar un polígono etiquetado.
 Dibuje la resultante desde el origen hasta la
punta del último vector y note el cuadrante de
la resultante.
 Escriba cada vector en notación i, j (Rx, Ry).
 Sume algebraicamente los vectores para
obtener la resultante en notación i, j. Luego
convierta a (R

64. Diferencia vectorial
Para vectores, los signos indican dirección. Por
tanto, cuando se resta un vector, antes de sumar
se debe cambiar el signo (dirección).
Ahora A – B: primero cambie el signo
(dirección) de B, luego sume el vector negativo.
B -B A
R’ -B
A A

65. Conclusión del Capítulo 3B - Vectores