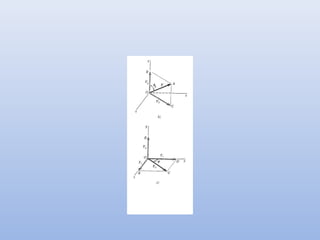
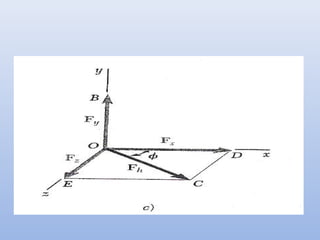
El documento describe los componentes rectangulares de una fuerza en el espacio tridimensional. Una fuerza F se puede descomponer en tres componentes rectangulares a lo largo de los ejes x, y, z (Fx, Fy, Fz) mediante el uso de ángulos θx, θy, θz. Se proporcionan ejemplos numéricos para ilustrar cómo calcular las componentes de una fuerza dada sus valores a lo largo de los ejes o sus ángulos con respecto a los ejes.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
UNIVERSIDAD PEDAGÓGICA EXPERIMENTAL LIBERTADOR
INSTITUTO PEDAGÓGICO DE BARQUISIMETO
“DR.LUIS BELTRÁN PRIETO FIGUEROA”
Componentes
rectangulares de una
fuerza en el espacio
Integrantes :
Rafael Martínez
Eleazar Peña
Eduardo Camacho

2. COMPONENTES
RECTANGULARES
DE UNA FUERZA EN EL
ESPACIO.
Una fuerza F en el espacio tridimensional se
puede descomponer en componentes
rectangulares Fx , Fy y Fz. Denotado por:

3. Fx = F cosθ x Fy = F cosθ y Fz = F cosθ z
Los ángulos que F forma, respectivamente, con los ejes x, y, y z se
tiene:
θ x ,θ y y θ z

4. Una fuerza de F se puede descomponer en una componente vertical
Fy y una componente horizontal Fh ; esta operación , se lleva
acabo en el plano OBAC siguiendo
las reglas desarrolladas en la primera parte de este capitulo.
*Las componentes escalares correspondientes son:
Fy= F cos θy Fh= F sen θy
*Fh se puede descomponer en dos componentes rectangulares Fx y
Fz a lo largo de las ejes x y z , respectivamente.

5. • Una fuerza de F se puede descomponer en una
componente vertical
Una fuerza de F se puede descomponer
en una componente vertical

7. • De esta forma, se obtiene las siguientes
expresiones para las componentes
escalares de Fx y Fz:
• Fx= Fh cos Ф = F sen θ y cos Φ
• Fz= Fh sen Φ = F sen θ y sen Φ
• La fuerza dada F se descompone en tres
componentes vectoriales rectangulares :
• Fx, Fy y Fz.

9. • Aplicando el teorema el teorema de Pitágoras a
los triángulos OBA y OCD:
• F²= (OA)² =(OB)²+(BA)²=F²y + F²h
• F²= (OC)² =(OD)²+(DC)²=F²x + F²z
• Eliminando Fh de estas dos escalares y
resolviendo para F, se obtiene la siguiente
relación entre la magnitud de F y sus
componentes escalares rectangulares :
• _______________
• F=√ Fx² + Fy² + Fz²

10. Problemas de vectores en el espacio.
• 1.- Una fuerza de 500 N forma ángulos de 60°, 45°, y
120° con los ejes x, y, y z respectivamente. Encuentre
las componentes Fx, Fy, y Fz de la fuerza.
• A) Fx = F cos θx = Fx = 500 N x cos 60°
• Fx = 500 N x 0.5 = 250 N.
• Fy = F cos θy = Fy = 500 N x cos 45°
• Fy = 500 N x 0.7071 = 354 N.
• Fz = F cos θz = Fz = 500 N x cos 120°
• Fz = 500 N x -0.5 = -250 N.

11. • Este último resultado es importante.
Siempre que una componente tenga un
ángulo obtuso, la componente tendrá un
signo negativo y viceversa.

12. • 2.- Una fuerza tiene las componentes Fx= 20 lb, Fy =
-30 lb, Fz = 60 lb. Determine la magnitud de la fuerza
resultante F, y los ángulos Θx, Θy y Θz.
• _______________
F=√ Fx² + Fy² + Fz²
________________________
F =√(20 lb)2 + (-30 lb)2 + (60 lb)2
_____________________________
F =√400 lb + 900 lb + 3600 lb
________
F = √4900 lb F = 70 lb.

13. • b) cos θx = Fx/F θx = 20 lb/70 lb = 0.2857.
• θx = cos-1 0.2857 = 73.4°.
• cos θy = Fy/F θy = - 30 lb/70 lb = -0.4285
• θy = cos -1 -0.4285 = 115.4°.
• cos θz = Fz/F θz = 60 lb/70 lb = 0.8571.
• θz = cos-1 0.8571 = 31°.

14. • 3.- Una fuerza en el espacio, tiene un valor de 2500 N, y
sus componentes Fx = -1060 N, Fy= +2120 N, Fz =
+795 N. Calcular los ángulos de dicha fuerza, con
respecto a los ejes x, y, y z (Θx, Θy, Θz).
• Cos Θx = Fx/F =- 1060 N/2500 N = - 0.424
• Θx = cos-1 - 0.424 = 115.1°.
• Cos Θy = Fy/F = 2120 N/2500 N = 0.848.
• Θy = cos-1 0.848 = 32°.
• Cos Θz = Fz/F = 795 N/2500 N = 0.318
• Θz = cos-1 0.318 = 71.5°.

15. • 4.- Determine la magnitud y dirección (Θx, Θy, Θz) de la
fuerza F= (260 N)i-(320 N)j+(800 N)k.
• ____________
• F = √Fx² + Fy² + Fz²
• ___________________________
• F = √(260 N)2 + (-320 N)2 + (800 N)2
• ____________________________
• F= √67600 N + 102400 N + 640000 N
• ________
• F = √810000 N
• F = 900 N.

16. • b) cos θx = Fx/F θx = 260 N/900 N =
0.2888. θx = cos-1 0.2888 = 73.2° .
• cos θy = Fy/F θy = - 320 N/900 N =
• -0.3555 θy = cos-1 – 0.3555 = 110.8°.
• cos θz = Fz/F θz = 800 N/900 N = 0.8888
• θz = cos-1 0.8888 = 27.3 °.

17. • 5.- Determine la magnitud y dirección de la fuerza F, (cosenos
directores) (Θx, Θy, Θz) dada por la ecuación:
• F= (320 N)i+(400 N)j-(250 N)k.
• ____________
• F = √Fx² + Fy² + Fz²
• ___________________________
• F = √(320 N)2 + (400 N)2 + (- 250 N)2
• ____________________________
• F= √102400 N + 160000 N + 62500 N
• ________
• F = √324900
• F = 570 N.

18. • b) cos θx = Fx/F θx = 320 N/570 N =
0.5614. θx = cos-1 0.5614 = 55.8° .
• cos θy = Fy/F θy = 400 N/570 N =
• 0.7017 θy = cos-1 0.7017 = 45.4 °.
• cos θz = Fz/F θz = -250 N/576 N =
• - 0.4340. θz = cos-1 -0.4340 = 116 °.

19. • 6.- El tirante de una torre, está anclado
por medio de un perno en A. La tensión
en dicho cable es de 2500 Newtons.
Determine las componentes Fx, Fy y Fz
de la fuerza que actúa sobre el perno,
conociendo que dx = -40 m, dy = +80 m,
dz = +30 m..
• A. Fx=-1060 N, Fy= +2120 N, Fz= 795 N

20. • ____________
• d = √dx² + dy² + dz²
• _______________________
• d = √(-40m)2 + (80 m)2 + (30 m)2
• ____________________________________
• d = √ 1600 m2 + 6400 m2 + 900 m2.
• ________
• d = √8900 m2.
• d = 94.33 m

21. • Fx = dx F
• d
• Fx = - 40 m (2500 N)
• 94.33 m
• Fx = - 0.4240 (2500) = -1060 N.
• Fy = dy F
• d
• Fy = 80 m (2500 N)
• 94.33 m
• Fy = 0.8480 (2500) = 2120 N.
• Fz = dz F
• d
• Fy = 30 m (2500 N)
• 94.33 m
• Fy = 0.3180 (2500) = 795 N.

22. • 7.- Una fuerza actúa en el origen de un sistema
coordenado en la dirección dada por los ángulos Θy=55°
y Θz=45°. Sabiendo que la componente de la fuerza en
x (Fx)= -500 lb, determine a) las otras componentes (Fy
y Fz) y la magnitud de la fuerza y b) el valor de Θx.
• Lo primero que hay que hallar es el ángulo faltante es
decir en este caso Θx.
• cos2 Θx + cos2 Θy + cos2Θz= 1 despejando
• cos2 Θx tenemos:
• cos2 Θx= 1- (cos2 Θy + cos2Θz).

23. • Sustituyendo valores:
• cos2 Θx = 1 - (cos2 55°+ cos2 45°)
• cos2 Θx= 1 - (0.3289+0.5)= 1-(0.8289)= 0.1711.
• Este resultado es el resultado del coseno
cuadrado de Θx, por lo tanto se le saca la raíz
cuadrada para obtener el valor del coseno de
Θx:
• ______
• cos Θx= √0.1711 = 0.4136.

24. • Una vez obtenido el valor del coseno de Θx
(0.4136) se procede a hallar el valor de la fuerza
resultante F, utilizando la componente Fx,
tomando su valor absoluto, es decir de forma
positiva. con la ecuación:
• Fx = F cos Θx. despejando F tenemos:
• F= Fx/cos Θx
• Sustituyendo valores: F= 500 lb /0.4136 =
• 1209 lb.

25. • Una vez obtenido el valor de la fuerza resultante
F, ya se pueden hallar las otras dos
componentes de la fuerza Fy y Fz con las
ecuaciones ya conocidas: Fy= FcosΘy y Fz=
Fcos Θz.
• Sustituyendo valores:
• Fy= 1209 N x cos 55° F y= 1209 N x 0.5735
• Fy= +694 N
• Fz= 1209 N x cos 45° F= 1209 N x 0.7071=
+855 lb.

26. • Finalmente se halla el valor del ángulo Θx, mediante la
siguiente ecuación:
• Fx= Fcos Θx. Despejando cos Θx= Fx/F. Sustituyendo
valores tenemos: cos Θx= -500 lb/1209 lb= cos Θx=
-0.4135.
• Θx= cos-1 -0.4135. Θx= 114.4°.
• Con el resultado anterior, se corrobora que cuando la
componente tiene un signo negativo, el ángulo
respectivo será obtuso y viceversa.
• Recapitulando: las respuestas son:
• Fy= +694 lb, Fz= +855 lb, b) F= 1209 lb, c) Θx= 114.4

27. • 8.- Una fuerza actúa en el origen de un sistema
coordenado en la dirección, definida por los ángulos,
Θx=69.3° y Θz=57.9°. Sabiendo que la componente y de
la fuerza es de Fy = -174 lb, determine: a) el ángulo Θy,
b) las componentes Fx y Fz de la fuerza y la magnitud
de la fuerza F.
• Lo primero que hay que hallar es el ángulo faltante es
decir en este caso Θy.
• cos2 Θx + cos2 Θy + cos2Θz= 1 despejando
• cos2 Θy tenemos:
• cos2 Θy= 1- (cos2 Θx + cos2Θz).

28. • Sustituyendo valores:
• cos2 Θy = 1 - (cos2 69.3°+ cos2 57.9°)
• cos2 Θy= 1 - (0.1249 + 0.2823)= 1-(0.4072)=
0.5928.
• Este resultado es el coseno cuadrado de Θy,
por lo tanto se le saca la raíz cuadrada para
obtener el valor del coseno de Θx:
• ______
• cos Θx= √0.5928 = 0.7699.

29. • Una vez obtenido el valor del coseno de Θy (0.7699)
se procede a hallar el valor de la fuerza resultante F,
utilizando la componente Fy, tomando su valor
absoluto, es decir de forma positiva. con la ecuación:
• Fy = F cos Θy. despejando F tenemos:
• F= Fy/cos Θy
• Sustituyendo valores: F= 174 lb /0.7699 =
• 226 lb.

30. • Una vez obtenido el valor de la fuerza resultante F,
ya se pueden hallar las otras dos componentes de la
fuerza Fx y Fz con las ecuaciones ya conocidas: Fx=
FcosΘx y Fz= Fcos Θz.
• Sustituyendo valores:
• Fx= 226 lb x cos 69.3 ° Fx= 226 lb x 0.3534
• Fx= 79.9 lb
• Fz= 226 lb x cos 57.9° Fz = 226 lb x 0.5313 =120.1 lb.

31. • Finalmente se halla el valor del ángulo Θy, mediante la
siguiente ecuación:
• Fy= Fcos Θy. Despejando cos Θy= Fy/F. Sustituyendo
valores tenemos: cos Θy= -174 lb/226 lb= cos Θy=
• -0.7699
• Θy= cos-1 -0.7699. Θy= 140.3°.
• Con el resultado anterior, se corrobora que cuando la
componente tiene un signo negativo, el ángulo
respectivo será obtuso y viceversa.
• Recapitulando: las respuestas son:
• Fx= 76.9 lb, Fz= 120.1 lb, b) F= 226 lb, c) Θy= 140.3°

32. • 9. Una fuerza actúa en el origen de un sistema
coordenado en la dirección definida por los ángulos
Θx=70.9°,y Θy=144.9°. Sabiendo que la componente z
de la fuerza es de Fz = -52 lb, determine: a) el ángulo
Θz y b) las componentes restantes (Fx y Fy) y la
magnitud de la fuerza F.
• A. a) 118.2°, b)Fx=36 lb, Fy=-90 lb, F=110 lb
• Lo primero que hay que hallar es el ángulo faltante es
decir en este caso Θz.
• cos2 Θx + cos2 Θy + cos2Θz= 1 despejando
• cos2 Θz tenemos:
• cos2 Θz= 1- (cos2 Θx + cos2Θy).

33. • Sustituyendo valores:
• cos2 Θz = 1 - (cos2 70.9°+ cos2 144.9°)
• cos2 Θz= 1 - (0.1070 + 0.6693)= 1-(0.7763)=
0.2237.
• Este resultado es el coseno cuadrado de Θz,
por lo tanto se le saca la raíz cuadrada para
obtener el valor del coseno de Θz:
• ______
• cos Θz= √0.2237 = 0.4729.

34. • Una vez obtenido el valor del coseno de Θz
(0.4729) se procede a hallar el valor de la fuerza
resultante F, utilizando la componente Fz,
tomando su valor absoluto, es decir de forma
positiva, con la ecuación:
• Fz = F cos Θz. despejando F tenemos:
• F= Fz/cos Θy
• Sustituyendo valores: F= 52 lb /0.4729 =
• 110 lb.

35. • Una vez obtenido el valor de la fuerza resultante
F, ya se pueden hallar las otras dos
componentes de la fuerza Fx y Fy con las
ecuaciones ya conocidas: Fx= FcosΘx y Fy=
Fcos Θy.
• Sustituyendo valores:
• Fx= 110 lb x cos 70.9 ° Fx= 110 lb x 0.3272
• Fx= 36 lb
• Fy= 110 lb x cos 144.9° Fy = 110 lb x - 0.8181 =
- 90 lb.

36. • Finalmente se halla el valor del ángulo Θz, mediante la
siguiente ecuación:
• Fz= Fcos Θz. Despejando cos Θz= Fz/F. Sustituyendo
valores tenemos: cos Θz= - 52 lb/110 lb= cos Θz=
• -0.4727
• Θz= cos-1 -04727. Θz= 118.2°.
• Con el resultado anterior, se corrobora que cuando la
componente tiene un signo negativo, el ángulo
respectivo será obtuso y viceversa.
• Recapitulando: las respuestas son:
• Fx= 36 lb, Fy= - 90 lb, b) F= 110 lb, c) Θz= 118.2°