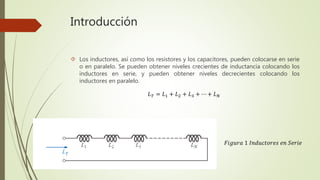
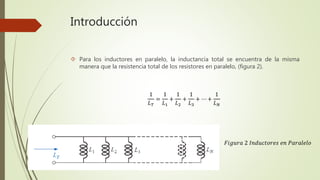
El documento describe diferentes tipos de inductores, incluyendo sus símbolos, apariencia y modelos equivalentes. También explica cómo colocar inductores en serie y paralelo para obtener niveles crecientes o decrecientes de inductancia total. Finalmente, presenta ejemplos de cálculos de corriente e inductancia para circuitos que contienen inductores.

1. Inductores en serie y
paralelo
Clase 11

2. Tipos de Inductores
 Los inductores, así como los capacitores, no son ideales. Asociadas con todo
inductor se tienen una resistencia igual a la resistencia de vueltas y una
capacitancia parasita debida a la capacitancia entre las vueltas de la bobina.
 Para incluir esos efectos, el circuito equivalente para el inductor es como se
muestra en la figura A
𝐹𝑖𝑔𝑢𝑟𝑎 𝐴 Modelo Completo
equivalente para un
inductor

3. Tipos de Inductores
 Sin embargo, para la mayoría de las aplicaciones consideradas, la capacitancia
parasita que aparece puede ser ignorada, resultando el siguiente modelo
equivalente.
𝐹𝑖𝑔𝑢𝑟𝑎 B Modelo practico
equivalente para un inductor

4. Símbolos
 La función principal del inductor, sin embargo, es introducir inductancia, no
resistencia o capacitancia, en una red. Por esta razón, los símbolos empleados para
la inductancia son como se muestra en la figura C
𝐹𝑖𝑔𝑢𝑟𝑎 C Símbolos del inductor

5. Apariencia
 Todos los inductores como los capacitores, pueden clasificarse bajo dos
encabezados generales: fijos y variables. En la figura D se muestran varios fijos y
variables.

6. Apariencia
Figura D Diversos tipos de
inductores:
(a) inductor toroidal de potencia, b)
inductores de montura superficial
sobre carretes , c) inductores
moldeados, d) inductores de filtro
de alta corriente, e) inductores de
filtro toroidales, f) inductores de
nucleo de aire.

7. Resumen

8. Resumen

9. Resumen

10. Resumen

11. Introducción
 Los inductores, así como los resistores y los capacitores, pueden colocarse en serie
o en paralelo. Se pueden obtener niveles crecientes de inductancia colocando los
inductores en serie, y pueden obtener niveles decrecientes colocando los
inductores en paralelo.
𝐿 𝑇 = 𝐿1 + 𝐿2 + 𝐿3 + ⋯ + 𝐿 𝑁
𝐹𝑖𝑔𝑢𝑟𝑎 1 𝐼𝑛𝑑𝑢𝑐𝑡𝑜𝑟𝑒𝑠 𝑒𝑛 𝑆𝑒𝑟𝑖𝑒

12. Introducción
 Para los inductores en paralelo, la inductancia total se encuentra de la misma
manera que la resistencia total de los resistores en paralelo, (figura 2).
1
𝐿 𝑇
=
1
𝐿1
+
1
𝐿2
+
1
𝐿3
+ ⋯ +
1
𝐿 𝑁
𝐹𝑖𝑔𝑢𝑟𝑎 2 𝐼𝑛𝑑𝑢𝑐𝑡𝑜𝑟𝑒𝑠 𝑒𝑛 𝑃𝑎𝑟𝑎𝑙𝑒𝑙𝑜

13. Introducción
 Para dos inductores en paralelo
𝐿 𝑇 =
𝐿1 𝐿2
𝐿1 + 𝐿2

14. Problemas
 Problema 1
 Reduzca la red de la figura 3 a su forma más simple.
𝐹𝑖𝑔𝑢𝑟𝑎 3

15. Problemas
 Solución
 Los inductores 𝐿2 𝑦 𝐿3 tienen el mismo valor y están en paralelo, resultando un
valor equivalente en paralelo de:
 La resultante de 0.6 H está entonces en paralelo con el inductor de 1.8H y
𝐿′ 𝑇 =
𝐿
𝑁
=
1.2𝐻
2
= 0.6𝐻
𝐿′′ 𝑇 =
𝐿′ 𝑇 𝐿4
𝐿′ 𝑇 + 𝐿4
=
0.6𝐻 1.8𝐻
0.6𝐻 + 1.8𝐻
= 0.45𝐻

16. Problemas
 Solución
 El inductor 𝐿1 está entonces en serie con el valor equivalente en paralelo, y
 La red reducida equivalente aparece en la figura 4
𝐿 𝑇 = 𝐿1 + 𝐿′′ 𝑇 = 0.56𝐻 + 0.45𝐻
𝐿 𝑇 = 1.01𝐻
𝐹𝑖𝑔𝑢𝑟𝑎 4

17. Circuitos R-L y R-L-C con entradas de cd
 Para todo fin práctico, un inductor se puede reemplazar por un corto circuito de cd
después que ha transcurrido un lapso mayor a cinco constantes de tiempo. Si en
los circuitos siguientes se supone que todas las corrientes y todos los voltajes han
alcanzado sus valores finales, la corriente a través de cada inductor se puede hallar
reemplazando cada inductor por un corto circuito. Por ejemplo, para los circuitos
de las siguientes figuras 5 y 6.

18. Circuitos R-L y R-L-C con entradas de cd
𝐹𝑖𝑔𝑢𝑟𝑎 5 Sustitución del corto circuito equivalente para el inductor

19. Circuitos R-L y R-L-C con entradas de cd
𝐼 =
𝐸1
𝑅1
=
10𝑉
2Ω
= 5𝐴

20. Circuitos R-L y R-L-C con entradas de cd
𝐹𝑖𝑔𝑢𝑟𝑎 6 Establecimiento de la red equivalente

21. Circuitos R-L y R-L-C con entradas de cd
 𝐼 =
𝐸
𝑅2||𝑅3
=
21𝑉
2Ω
= 10.5𝐴
 Aplicando la regla del divisor de corriente:
 𝐼1 =
𝑅3 𝐼
𝑅3+𝑅2
=
6Ω 10,5Ω
6Ω+3Ω
=
63𝐴
9
= 7𝐴

22. Circuitos R-L y R-L-C con entradas de cd
 En lo siguientes ejemplos se supondrá que el voltaje en los
capacitores y la corriente a través de los inductores han
alcanzando sus valores finales. Bajo esas condiciones, los
inductores se pueden reemplazar por corto circuitos y los
capacitores por circuitos abiertos.

23. Problemas Complementarios
 Problema 1. Encuentre la corriente 𝐼𝐿, y el voltaje 𝑉𝐶 para la red de la figura
6

24. Problemas Complementarios
 Solución.

25. Problemas Complementarios
 Solución.
 𝐼𝐿 =
𝐸
𝑅1+𝑅2
=
10𝑉
5Ω
= 2𝐴
 𝑉𝐶 =
𝑅2 𝐸
𝑅2+𝑅1
=
3Ω 10𝑉
3Ω+2Ω
= 6𝑉

26. Problemas Complementarios
 Problema 2. Encuentre las corrientes 𝐼1 e 𝐼2 y los voltajes 𝑉1 𝑦 𝑉2 para la
red de la figura 7

27. Problemas Complementarios
 Solución.
Sustitución de los corto circuitos equivalentes para los inductores
Y circuitos abiertos equivalentes

28. Problemas Complementarios
 Solución.
 𝐼1 = 𝐼2
 𝐼1 =
𝐸
𝑅1+𝑅3+𝑅5
=
50𝑉
2Ω+1Ω+7Ω
=
50𝑉
10Ω
= 5𝐴
 𝑉2 = 𝐼2 𝑅5 = 5𝐴 7Ω = 35𝑉
 Aplicando la regla del divisor de voltaje:
 𝑉1 =
𝑅3+𝑅5 𝐸
𝑅1+𝑅3+𝑅5
=
1Ω+7Ω 50𝑉
2Ω+1Ω+7Ω
=
8Ω 50𝑉
10Ω
= 40𝑉

29. Energía Almacenada por un inductor
 El inductor ideal, así como el capacitor ideal, no disipa la energía eléctrica
que se le suministra; la almacena en forma de campo magnético. Una
grafica del voltaje, la corriente y la potencia en un inductor se muestra en
la figura A durante la formación del campo magnético que rodea al
inductor. La energía almacenada se representa por el área sombreada bajo
la curva de potencia. Usando el calculo, se puede mostrar que la
evaluación del área bajo la curva resulta en:
𝑊𝑎𝑙𝑚𝑎𝑐𝑒𝑛𝑎𝑑𝑎 =
1
2
𝐿𝐼 𝑚
2
𝐽𝑜𝑢𝑙𝑒𝑠, 𝐽

30. Energía Almacenada por un inductor
Figura A. Curva de potencia para un elemento inductivo bajo
condiciones transitorias

31. Energía Almacenada por un inductor
 Problema. Encuentre la energía almacenada por el inductor en el circuito
de la figura cuando la corriente a través de el ha alcanzado su valor final.

32. Energía Almacenada por un inductor
 Solución.

33. Energía Almacenada por un inductor
 Solución.
 𝐼 𝑚 =
𝐸
𝑅1+𝑅2
=
15𝑉
3Ω+2Ω
=
15𝑉
5Ω
= 3𝐴
 𝑊𝑎𝑙𝑚𝑎𝑐𝑒𝑛𝑎𝑑𝑎 =
1
2
𝐿𝐼 𝑚
2
=
1
2
6 × 10−3
𝐻 3𝐴 2
=
54
2
× 10−3
𝐽 = 27𝑚𝐽