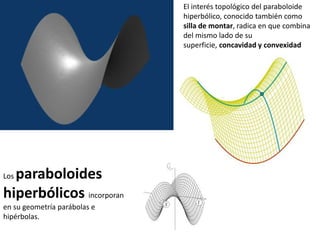
El documento clasifica los volúmenes en reglados y de doble curvatura, explicando sus características geométricas y ejemplos, como los poliedros, cilindros y conos. Además, aborda los sólidos platónicos y la generación de superficies a partir de movimientos de líneas rectas y curvas. Se destacan aplicaciones en la construcción y la complejidad de volúmenes de curvatura avanzada.

1. Clases de volúmenes
Javier Echeverri
(20111031 v1)

2. A. Sistema de clasificación
B. Volúmenes Reglados
C. Volúmenes de doble curvatura

3. Los volúmenes por su desarrollo geométrico, el cual se expresa en la visualidad de su
superficie, se clasifican en dos grandes grupos:
reglados y de doble curvatura.
Los volúmenes reglados son aquellos Los volúmenes de doble curvatura son
engendrados por una línea recta en aquellos engendrados por una línea
movimiento. Aunque pueden presentar curva en movimiento. No presentan
superficies curvas, siempre tienen algún ningún componente recto, como la
componente recto, como el cilindro. esfera.

4. El sistema de clasificación aquí propuesto toma como base los conceptos sobre superficies en el espacio 3D expuestos por
B. Leighton Wellman, en su Compendio de geometría descriptiva para técnicos, Editorial Reverté, Barcelona, 1983.

5. Los poliedros son una Sólidos platónicos
variante particular de los volúmenes
reglados. Son aquellos que no
presentan un solo componente curvo en
su superficie envolvente, la cual está
compuesta exclusivamente de
superficies planas, regulares o
irregulares.
Cuándo todas las caras del poliedro son
regulares e iguales, como triángulos
equiláteros, cuadrados o hexágonos, se
denominan sólidos platónicos. Cuando
no cumplen esta condición, se
denominan genéricamente como
prismas.
Prismas

6. Lossólidos platónicos son una singularidad de la geometría, solo son 5, y
constituyen la única posibilidad de cerrar un sólido convexo con polígonos regulares de igual
forma. Reciben este nombre en honor al filósofo griego Platón, a quien se atribuye haberlos
estudiado, en primera instancia.

7. Los sólidos platónicos
8 triángulos
4 triángulos
6 cuadrados equiláteros
equiláteros
o hexaedro
12 pentágonos 20 triángulos
equiláteros

8. Poliedros
truncados
convexos
obtenidos a partir de truncar los
vértices de los sólidos platónicos

9. Troncoicosaedro,
cuya variante topológica inflado en esfera, produce el famoso balón de fútbol.

10. Poliedros regulares no convexos (cóncavos), generalmente llamados estrellados

11. Los prismas son poliedros que en términos generales no poseen caras iguales

12. En la categoría de los prismas también
pueden incluirse las
pirámides

13. Tanto prismas como pirámides pueden ser
rectos, oblicuos o truncados.

14. Otra variante de los volúmenes reglados son los
volúmenes de simple curvatura,
que tienen un componente curvo en su superficie, pero también un componente recto, como el
cono y el cilindro.
Se engendran por el desplazamiento de una línea recta llamada generatriz, que se desplaza por
una línea curva llamada directriz.

15. Los volúmenes de simple curvatura pueden ser de tres clases:
cilindros, conos y convolutas.

16. Generación de las superficies
de simple curvatura

17. Una de sus características es que se
desenrollan, esto es, pueden
construirse a partir del doblez de una
superficie plana.

18. La tercera y última clase de volúmenes reglados son losalabeados , volúmenes que se
producen también por una generatriz recta en una directriz curva, cuyo desarrollo en el espacio
hace que no se puedan desenrollar.

19. Si bien no se pueden
desenrrollar, la
posibilidad de ser
generados a partir de
elementos rectos, los
hacen de una gran
aplicación en la
construcción.

20. Construcción de una
superficie alabeada a partir
de elementos rectos.

21. Los helicoides son también volúmenes construidos a partir de superficies alabeadas

22. La estructura del ADN es una doble hélice, enrolladas una en la otra.

23. Losvolúmenes de revolución son volúmenes de doble
curvatura, engendrados por una generatriz curva, que gira alrededor de un eje.
En la ilustración, e representa el eje, y g la generatriz.

24. Si se secciona el cono en
posiciones diferentes en el
espacio, dichas secciones
producen las llamadas
curvas
cónicas, que son la
base generatriz de las
superficies de revolución.

25. Laesfera es el volumen regular por excelencia, producto del
giro de un circulo en su diámetro

26. Elesferoide identifica el
volumen cuya superficie es el
producto de girar
una elipse alrededor de uno de sus
ejes principales.

27. Las parábolas y las
hipérbolas dan lugar a una
rica variedad de superficies
curvas.

28. Unparaboloide de
revolución, es el
volúmen cuya superficie es
generada por la rotación de
una parábola alrededor de su eje
de simetría

29. hiperboloide de
El
revolución, es el volúmen
cuya superficie es generada por la
rotación de una hipérbola alrededor de
su eje de simetría

30. El interés topológico del paraboloide
hiperbólico, conocido también como
silla de montar, radica en que combina
del mismo lado de su
superficie, concavidad y convexidad
paraboloides
Los
hiperbólicos incorporan
en su geometría parábolas e
hipérbolas.

31. Eltoro anular es una de
los volúmenes de revolución
topológicamente más importantes,
producto del desplazamiento de un
círculo a lo largo de una trayectoria
circular.

32. Finalmente tenemos los
doble
volúmenes de
curvatura
por
evolución, que
representan el mayor nivel
de complejidad
geométrica, y son el
producto de superficies
curvas producidas por
directrices y generatrices
cambiantes.

33. La complejidad de su geometría implica problemas de representación en el plano, la cual debe
realizarse a partir de una gran cantidad de dibujos.

34. CLASES DE VOLÚMENES
JAVIER ECHEVERRI
Profesor Titular
Escuela de Arquitectura
Facultad de Artes Integradas
Universidad del Valle
Cali - Colombia
Universidad
del Valle
(20111031 – v1)