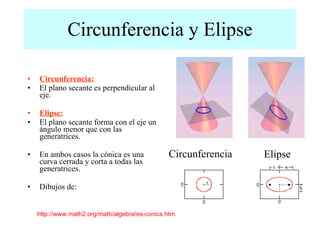
El documento describe las aplicaciones de las diferentes curvas cónicas como la circunferencia, la hipérbola y la parábola. Menciona ejemplos históricos como Kepler, Arquímedes y Galileo y sus contribuciones al estudio de las cónicas. También describe aplicaciones modernas como el puente sobre las cataratas de Niágara, el faro de Cabo Mayor, el faro de Alejandría y la nave espacial Voyager. Finalmente, define una superficie cónica y explica las diferencias entre una circunferencia/elipse

1. APLICACIONES (Resumen del fichero de 1º de Bachillerato del IES “Alberto Pico” LAS CÓNICAS

2. Aplicaciones de la circunferencia

3. Aplicaciones de la circunferencia

4. Kepler 1571-1630 Alemania http://www.arrakis.es/~mcj/conicas.htm

6. Aplicaciones de la hipérbola

7. Arquímedes, nació en Siracusa, Sicilia en el año 287 AC y murió en el 212 AC

9. Galileo 1564-1642 http:// www.arrakis.es / ~mcj / conicas.htm Tiro parabólico

10. Puente sobre las cataratas de Niágara Construido por Leonardo Torres Quevedo

11. El Voyager

13. Aplicaciones parábolas

14. Aplicaciones de las parábolas Faro de Cabo Mayor

15. Faro de Alejandría 290 AC

16. SECCIONES CÓNICAS Bloque II * Tema 072

17. SUPERFICIE CÓNICA Una superficie cónica es aquella que se obtiene al hacer girar una recta g , llamada generatriz , alrededor de otra recta e , llamada eje , cuando g y e son secantes. El punto de corte de ambas rectas es el vértice V de la superficie. Al cortar a la superficie así formada por un plano se obtienen secciones que se llaman cónicas . Cuando el plano cortante contiene al vértice se obtienen las llamadas cónicas degeneradas , que son un punto , una recta o un par de rectas secantes . Generatriz Eje Vértice

18. Cónicas degeneradas Punto Recta Rectas secantes α < β α = β α > β α β α β α β

19. Circunferencia y Elipse Circunferencia: El plano secante es perpendicular al eje. Elipse: El plano secante forma con el eje un ángulo menor que con las generatrices. En ambos casos la cónica es una curva cerrada y corta a todas las generatrices. Dibujos de: Circunferencia Elipse http:// www.math2 . org / math /algebra/es- conics.htm

20. Parábola e Hipérbola Parábola Hipérbola http:// www.math2 . org / math /algebra/es- conics.htm Parábola: El plano secante es paralelo a una generatriz, cortando a una sola de las hojas de la superficie cónica. Hipérbola: El plano secante forma con el eje un ángulo menor que con las generatrices y corta a las dos hojas de la superficie cónica. En ambos casos la cónica es una curva abierta y no corta a todas las generatrices. Dibujos de: