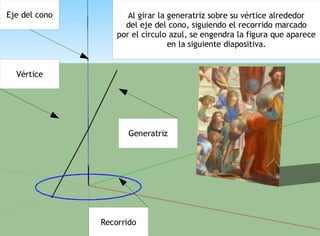
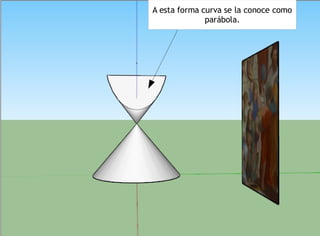
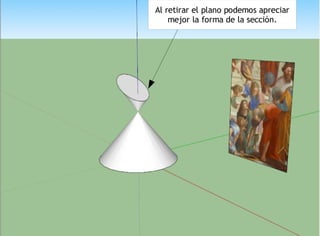
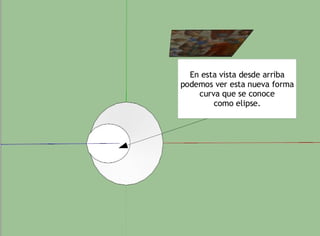
Las cónicas son una familia de curvas que se obtienen al cortar un cono de revolución con un plano de diferentes formas, dando lugar a secciones como la hipérbola, parábola, elipse y circunferencia. Los matemáticos griegos ya estudiaban estas curvas creadas al cortar un cono.

1. Las cónicas
Dentro del amplio campo de la geometría en el apartado de lugares geométricos
ocupa un papel destacado el estudio de las cónicas.
Los matemáticos griegos ya conocían esta familia de curvas las cuales obtenían a
partir de las secciones que en un cono de revolución crea un plano que corta al
mismo de distintas formas.
En primer lugar vamos a ver en la siguiente diapositiva como se genera dicha figura.

2. Eje del cono Al girar la generatriz sobre su vértice alrededor
del eje del cono, siguiendo el recorrido marcado
por el círculo azul, se engendra la figura que aparece
en la siguiente diapositiva.
Vértice
Generatriz
Recorrido

3. La figura del espacio engendrada
por el giro de la generatriz
consta de dos conos unidos por el vértice.
Cada uno de ellos se denomina hoja
de la superficie cónica.

4. Cuando un plano paralelo al eje
corta a la superficie cónica
este provoca en la misma
una sección que adopta
una forma curva.

5. Si retiramos el plano podemos apreciar mejor
la forma.

6. A esta primera sección que hemos obtenido
se le llama hipérbola, se puede apreciar
que es una curva que consta de dos ramas.

7. Aquí tenemos la representación de la
hipérbola en un sistema de ejes cartesianos
y su ecuación.

8. Si el plano corta ahora a una de las hojas
de forma paralela a la generatriz obtenemos
otra sección diferente.

9. Si retiramos el plano podemos apreciar
mejor la forma que adopta la sección.

10. A esta forma curva se la conoce como
parábola.

11. Aquí tenemos la representación
de la parábola en un sistema
de ejes cartesianos junto a su ecuación.

12. Si el plano corta a la figura de forma oblicua
atravesándola transversalmente,
obtenemos otra sección diferente
a las anteriores.

13. Al retirar el plano podemos apreciar
mejor la forma de la sección.

14. En esta vista desde arriba
podemos ver esta nueva forma
curva que se conoce
como elipse.

15. Aquí tenemos la elipse representada
en un sistema de ejes cartesianos
junto a su ecuación.

16. Para terminar veamos lo que ocurre
cuando un plano perpendicular al eje
corta a la superficie cónica en una
de sus hojas.

17. Al retirar el plano la forma
de la sección que deja nos debe
resultar familiar.

18. En esta vista desde arriba
podemos apreciar que la curva
que se ha creado es una
circunferencia.

19. Aquí tenemos la representación
de la circunferencia
en un sistema de ejes cartesianos
junto a su ecuación.