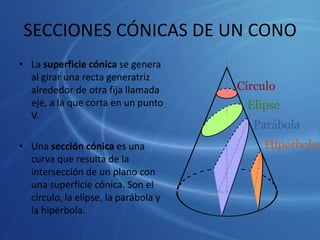
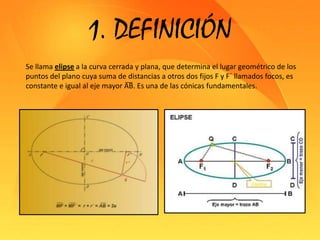
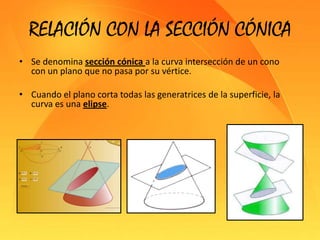
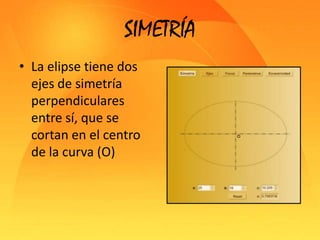
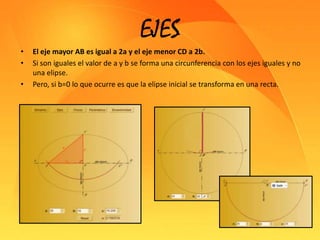
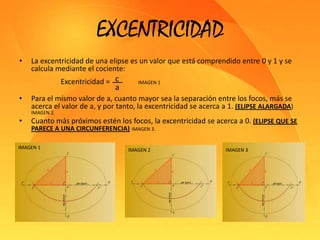
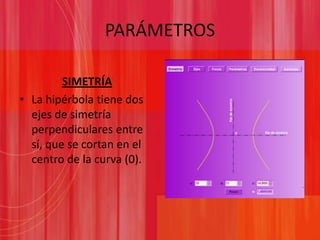
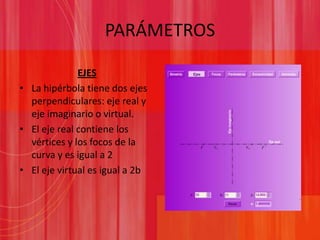
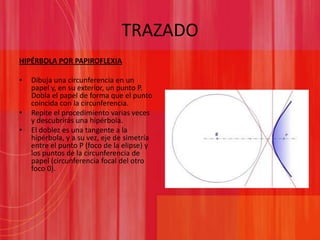
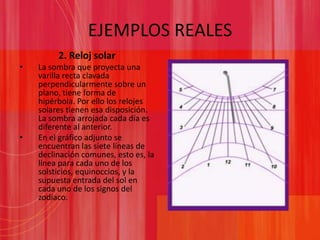
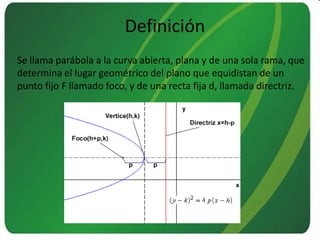
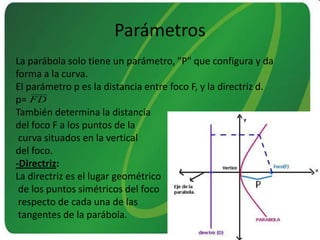
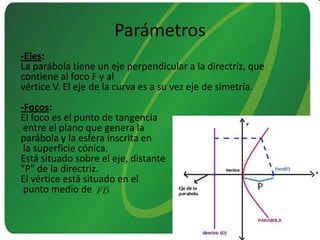
Este documento presenta información sobre las secciones cónicas (elipse, hipérbola y parábola). Define cada curva, explica sus parámetros clave como ejes, focos y excentricidad, y métodos para trazarlas. También proporciona ejemplos de cómo se usan estas curvas en aplicaciones como órbitas planetarias, telescopios, relojes solares y navegación.

1. CÓNICASCRISTINA LÓPEZ MUÑOZJENNIFER PEDRAZA NOVALBOSMª JOSÉ GÓMEZ GUTIÉRREZ1º BACHILLERATO CCNN1-12-2010 MATEMÁTICAS

2. ÍNDICESecciones cónicas de un conoElipse Definición, parámetros, estudio analítico, trazado y ejemplos realesHipérbolaDefinición, parámetros, estudio analítico, trazado y ejemplos realesParábolaDefinición, parámetros, estudio analítico, trazado y ejemplos realesActividades del vídeo “Del baloncesto a los cometas”Opinión personal acerca del trabajoBibliografía

3. SECCIONES CÓNICAS DE UN CONOLa superficie cónica se genera al girar una recta generatriz alrededor de otra fija llamada eje, a la que corta en un punto V.Una sección cónica es una curva que resulta de la intersección de un plano con una superficie cónica. Son el círculo, la elipse, la parábola y la hipérbola.

4. ELIPSEMARÍA JOSÉ GÓMEZ GUTIÉRREZ

5. 1. DEFINICIÓNSe llama elipse a la curva cerrada y plana, que determina el lugar geométrico de los puntos del plano cuya suma de distancias a otros dos fijos F y F´ llamados focos, es constante e igual al eje mayor AB. Es una de las cónicas fundamentales.

6. RELACIÓN CON LA SECCIÓN CÓNICASe denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. Cuando el plano corta todas las generatrices de la superficie, la curva es una elipse.

7. 2. PARÁMETROS2 a= eje mayor AB2b = eje menor CD2c=distancia focal FF´ Los tres parámetros configuran un triángulo rectángulo por lo que se cumple: a2=b2+c2Existen 4 tipos de parámetros: simetría, ejes, focos y excentricidad.

8. SIMETRÍALa elipse tiene dos ejes de simetría perpendiculares entre sí, que se cortan en el centro de la curva (O)EJESEl eje mayor AB es igual a 2a y el eje menor CD a 2b.

9. Si son iguales el valor de a y bse forma una circunferencia con los ejes iguales y no una elipse.

10. Pero, si b=0 lo que ocurre es que la elipse inicial se transforma en una recta.FOCOSLos focos son los puntos de tangencia entre el plano que genera la elipse y las esferas inscritas en la superficie cónica. Son F y F´.Los focos están situados sobre el eje mayor distantes “a” de los extremos del eje menor.La distancia focal F-F´ es igual a 2c.

11. La excentricidad de una elipse es un valor que está comprendido entre 0 y 1 y se calcula mediante el cociente:cPara el mismo valor de a, cuanto mayor sea la separación entre los focos, más se acerca el valor de a, y por tanto, la excentricidad se acerca a 1. (ELIPSE ALARGADA) IMAGEN 2.Cuanto más próximos estén los focos, la excentricidad se acerca a 0. (ELIPSE QUE SE PARECE A UNA CIRCUNFERENCIA)IMAGEN 3.EXCENTRICIDADExcentricidad =IMAGEN 1 aIMAGEN 1IMAGEN 2IMAGEN 3

12. 3. TRAZADOMÉTODO DEL JARDINERO: Para trazar elipses de grandes dimensiones podemos usar una cuerda de longitud igual al eje mayor, colocamos sus extremos sobre los focos y estiramos la cuerda para dibujar la curva.PASO 1.PASO 3.PASO 2.

13. 4. ESTUDIO ANALÍTICOLa ecuación reducida de la elipse, tras sus cálculos, es la siguiente: x2 y2Con la fórmula reducida de la elipse podemos conocer las coordenadas de todos sus puntos.+= 1a2 b2

14. 5. EJEMPLOS REALESLas curvas cónicas y, en este caso, la elipse tienen numerosas aplicaciones no sólo en el ámbito matemático ni de la ciencia, sino en otros que en apariencia parecen que no han recibido influencia de ellas. Estos otros ámbitos en los que se utilizan las elipses son el deporte, la astronomía, la arquitectura y la forma de los alimentos, entre otros.

15. ÓRBITAS PLANETALESEstas formas cónicas son importantes en astronomía, ya que en dos cuerpos masivos que interactúan según la ley de gravitación universal, sus trayectorias describen elipses si su centro de masa se considera en reposo y están relativamente próximas. Las órbitas de los planetas del sistema solar al rotar alrededor del sol son elípticas. El sol estaría situado en uno de sus focos y la excentricidad es próxima a 0, es decir, se acerca bastante a una circunferencia.

16. FORMAS CIRCULARESLa representación de cualquier forma circular que no observemos frontalmente, es una elipse.Esto se puede dar por ejemplo al observar (desde una perspectiva no frontal) las ondas en un charco de agua al tirar algún objeto pequeño, un plato, un disco, ruedas o señales de tráfico siempre y cuando sean redondos.

17. ARQUITECTURA ELIPSOIDALLas bóvedas elipsoidales permiten a dos personas A y B situadas en sus focos teóricos, mantener una conversación sin que las personas más próximas se enteren.Esta técnica ha sido utilizada desde los romanos en sus termas y baños públicos o en arcos con forma elipsoidal.Cúpulas elipsoidales conocidas son la de Statuary Hall del Capitolio de Washington o la cámara de los secretos de la Alhambra de Granada.

18. ILUMINACIÓN & DISEÑOLa forma que adopta la proyección de un foco puntual sobre un plano oblicuo, respecto a su eje de iluminación, es una elipse.La revolución de una elipse sobre su eje genera un elipsoide, de los que encontramos varios ejemplos en la naturaleza y varios objetos creados por el hombre. Ejemplos de ello, son el melón y el balón de rugby.

19. DISEÑOLa forma elíptica es un recurso arquitectónico muy utilizado en todas las manifestaciones del diseño.Se puede comprobar en el diseño industrial, en la pintura, en la arquitectura, en el diseño gráfico, etc.

20. HIPÉRBOLAJENNIFER PEDRAZA NOVALBOS

21. DEFINICIÓNSe llama Hipérbola a la curva cerrada y plana, que determina el lugar geométrico de los puntos del plano cuya diferencia de distancias a otros dos fijos F y F’ llamamos focos, es constante e igual al eje real V1 V2.La diferencia de los radios vectores r y r’ es igual al eje mayor V1V2.

22. PARÁMETROS2a= eje real V1V22b =eje virtual2c= distancia focal FF’Los tres parámetros configuran un triángulo rectángulo por lo que se cumple: c2 = b2+a2

23. PARÁMETROSSIMETRÍALa hipérbola tiene dos ejes de simetría perpendiculares entre sí, que se cortan en el centro de la curva (0).

24. PARÁMETROSEJESLa hipérbola tiene dos ejes perpendiculares: eje real y eje imaginario o virtual.El eje real contiene los vértices y los focos de la curva y es igual a 2El eje virtual es igual a 2b

25. PARÁMETROSFOCOSLos Focos son los puntos de tangencia entre el plano que genera la hipérbola y las esferas inscritas en la superficie cónica.Están situados sobre el eje real distantes “c” del centro de la curva.La distancia focal F-F’ es igual a 2c

26. PARÁMETROSEXCENTRICIDADEs la razón c/a (inversa del coseno del ángulo de la asíntota) y en la hipérbola su valor oscila entre uno e infinito.Es la razón de distancias de un punto cualquiera de la curva al foco y a la directriz correspondiente.

27. PARÁMETROSASÍNTOTASLas asíntotas son las tangentes a la hipérbola en puntos del infinito. Son simétricas respecto a los ejes y pasan por el centro 0.Cuando forman con los ejes ángulos de 45º, la hipérbola se denomina “equilátera”, y se cumple que a=b.

28. TRAZADOHIPÉRBOLA POR PAPIROFLEXIADibuja una circunferencia en un papel y, en su exterior, un punto P. Dobla el papel de forma que el punto coincida con la circunferencia.Repite el procedimiento varias veces y descubrirás una hipérbola.El doblez es una tangente a la hipérbola, y a su vez, eje de simetría entre el punto P (foco de la elipse) y los puntos de la circunferencia de papel (circunferencia focal del otro foco 0).

29. ESTUDIO ANALÍTICO(FÓRMULA)x2y2Con la fórmula reducida de la hipérbola podemos conocer las coordenadas de todos sus puntos.Cambiando sobre el gráfico los valores de las coordenadas (x, y), y de los parámetros de la hipérbola (a, b, c), observamos la posición que adopta el punto P.-= 1a2 b2

30. EJEMPLOS REALES1. IluminaciónLa luz que proyecta la lámpara troncocónica sobre una pared paralela a su eje, tiene forma de hipérbola.

31. EJEMPLOS REALES2. Reloj solarLa sombra que proyecta una varilla recta clavada perpendicularmente sobre un plano, tiene forma de hipérbola. Por ello los relojes solares tienen esa disposición. La sombra arrojada cada día es diferente al anterior. En el gráfico adjunto se encuentran las siete líneas de declinación comunes, esto es, la línea para cada uno de los solsticios, equinoccios, y la supuesta entrada del sol en cada uno de los signos del zodiaco.

32. EJEMPLOS REALES3. LORAN, navegación hiperbólica.La aeronave dotada de un equipo Loran proporciona información de posición midiendo la diferencia de tiempo en microsegundos, entre la llegada de dos señales de radio desde dos estaciones transmisoras de tierra.La aeronave puede estar situada en cualquier punto de la hipérbola. Pues en cada uno de sus puntos, la diferencia de tiempo en la llegada de las estaciones LORAN, es constante (definición de hipérbola).Para conocer exactamente la posición del avión sobre la hipérbola será necesario sintonizar otro grupo LORAN para llevar a cabo el mismo procedimiento.La intersección de las dos hipérbolas será la posición del avión.

33. EJEMPLOS REALES4. Telescopios de tipo Cassegrain.Fue inventado en 1672 por el físico francés N. Cassegrain. La incorporación del espejo hiperbólico, reduce considerablemente su tamaño.Telescopios de tipo Cassegrain están en funcionamiento en algunos de los observatorios astronómicos más importantes del mundo.La Hipérbola tiene propiedades de reflexión análogas a las de la elipse. Si proyectamos un haz de luz desde un foco, por ejemplo de f, se reflejará en la hipérbola en dirección del foco f’.Este principio se usa en los telescopios del tipo Cassegrain.

34. ParábolasCristina López Muñoz

35. DefiniciónSe llama parábola a la curva abierta, plana y de una sola rama, que determina el lugar geométrico del plano que equidistan de un punto fijo F llamado foco, y de una recta fija d, llamada directriz.

36. ParámetrosLa parábola solo tiene un parámetro, "P" que configura y daforma a la curva.El parámetro p es la distancia entre foco F, y la directriz d.p=También determina la distancia del foco F a los puntos de la curva situados en la vertical del foco.-Directriz:La directriz es el lugar geométrico de los puntos simétricos del foco respecto de cada una de las tangentes de la parábola.

37. Parámetros-Ejes:La parábola tiene un eje perpendicular a la directriz, que contiene al foco F y alvértice V. El eje de la curva es a su vez eje de simetría.-Focos:El foco es el punto de tangencia entre el plano que genera la parábola y la esfera inscrita en la superficie cónica.Está situado sobre el eje, distante "P" de la directriz.El vértice está situado en el punto medio de

38. Trazado por haces proyectivos1.Se sitúan los datos con los que contamos, y se determina el punto P’,simétrico de P respecto del eje. Por el vértice A de la curva se traza unaperpendicular al eje, y por P y P’ se trazan las paralelas al eje; donde estascortan a la perpendicular se obtienen los puntos M y N.2.Se dividen MP y AM en un número de partes iguales, por ejemplo seis. Porlas divisiones obtenidas sobre AM se trazan paralelas al eje. Se unen con elvértice A los puntos de la división MP, y donde estas rectas cortan a lasparalelas se obtienen los puntos 1, 2, 3, etc. Los puntos 1’, 2’,3’, etc., se hallanpor simetría.3. Uniendo los puntos así determinados con una línea continua, se obtiene laparábola pedida.

39. Estudio analíticoEcuación reducida de la parábola: y2=2pxCon la fórmula reducida de la parábola podemos conocer las coordenadas de todos sus puntos.Ejemplos realesSuperficies parabólicas: Cuando la forma de la superficie es parabólica todos los rayos que llegan paralelos al eje de la parábola se reflejan pasando por un mismo punto que se denomina "foco“-Antenas parabólicas-Espejos parabólicos-Focos

40. Iluminación:La forma que adopta la proyecciónde un foco puntual sobre un ladoparalelo a un lado del foco.Trayectoria de proyectiles:La trayectoria que describen losproyectiles (despreciando elrozamiento con el aire)

41. Diseño:La parábola es utilizada frecuentemente en la arquitectura moderna y endiseño industrial.

42. Actividades del vídeo “Del baloncesto a los cometas”Hoy vamos a hablar de las curvas que han atraído la atención de los matemáticos hace 2000 años. Éstas son las parábolas, círculos, elipses e hipérbolas.Las curvas mencionadas que se ven en el vaso son el círculo y la elipse.El instrumento que se utiliza para dibujar las cónicas en la pared es una lámpara desde distintas posiciones.Los estudios de un matemático en apariencia no parecen útiles, pero en realidad sí. Estos conceptos matemáticos tuvieron utilidad en la ciencia a partir del siglo IV a.C. como los relojes solares.Menecmo de Pérgamo es el autor del más importante tratado de la antigüedad dedicado a las cónicas.El nombre de cónicas procede de su descubrimiento al ver que cortando un cono se pueden obtener las curvas.

43. Actividades del vídeo “Del baloncesto a los cometas”7. Johannes Kepler utilizó por primera vez las cónicas, las utilizó para estudiar el movimiento de los astros como la elipse de Marte, situando al sol en uno de sus focos.8. La propiedad geométrica que caracteriza a las elipses es que la suma de las distancias de cada punto de la elipse a los dos focos es siempre la misma.9. Las elipses las encontramos en el metro cuando dos personas hablan desde diferentes andenes, en las bóvedas, en el balón de rugby, en las piedras erosionadas,…10. La parábola aparece en el baloncesto al lanzar canasta, al lanzar la llama en los Juegos Olímpicos, en el agua de las fuentes,…11. Galileo la descubrió pero fue Newton quien la desarrollo con las ecuaciones de la gravitación universal.

44. OPINIÓN PERSONALMª JOSÉ GÓMEZ GUTIÉRREZ: este trabajo me ha parecido interesante porque me ha ayudado a conocer aspectos matemáticos que no conocía, sobre todo, la elipse. Además me ha ayudado a comprobar que tienen una aplicación práctica en las cosas de la vida cotidiana que veo a diario, y no solo la aplicación matemática como creía.JENNIFER PEDRAZA NOVALBOS: Este trabajo sobre las cónicas (aunque no es la parte de matemáticas que me parece más entretenida) me ha ayudado a conocer algo más, estos tipos de secciones cónicas.CRISTINA LÓPEZ MUÑOZ: Este trabajo ha sido una forma interesante de aprender cosas sobre las cónicas de una forma distinta, práctica y entretenida.

45. BIBLIOGRAFÍALa información obtenida procede de las siguientes páginas web:http://es.wikipedia.org/wiki/Elipsehttp://es.wikipedia.org/wiki/Secci%C3%B3n_c%C3%B3nicahttp://w3.cnice.mec.es/eos/MaterialesEducativos/mem2006/curva_conicas/index.htmlBiblioteca de consulta Encarta 2005http://www.ite.educacion.es/w3/eos/MaterialesEducativos/mem2006/curva_conicas/pdf/apuntes.pdf