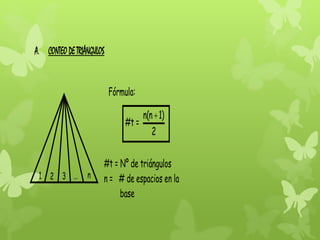
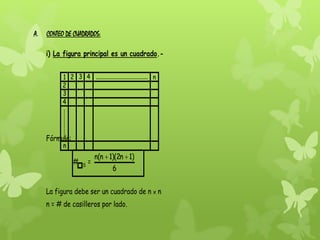
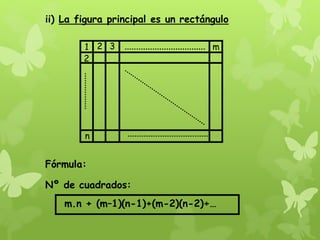
El documento presenta métodos para contar figuras geométricas. Explica el método combinatorio para contar triángulos en una figura mediante la asignación de números a sus partes. También presenta fórmulas para contar segmentos, triángulos, cuadriláteros, cuadrados, cubos y paralelepípedos dependiendo del número de espacios o casilleros de la figura.

1. CONTEO DE
FIGURAS
Lic. Jackeline Arias Romero

2. CONTEO DE FIGURAS
Para algunos de estos problemas se
dispone de ciertos métodos
sistemáticos o fórmulas
preestablecidas, mientras que para
otros solo podemos contar con
nuestra intuición e imaginación para
obtener la solución. Haremos
entonces un estudio por separado de
los casos que se conoce.

3. 1.- MÉTODO COMBINATORIO
El presente método consiste en anotar un
número o símbolo en c/u de las partes de
la figura, de modo que cada nueva figura
que detectemos quede asociada a un
número o combinación de números. Luego
contamos las combinaciones anotadas y el
resultado será la cantidad pedida.

4. EJEMPLO
¿Cuántos triángulos hay en esta figura?

5. Solución .Colocamos un dígito a cada parte:
1
Los triángulos son:
2
8
3
7
4
6
5
De (1) : 1; 2; 3; 4; 5; 6; 7; 8= 8
De (2) 12; 34; 56; 78
=4
De (5) : 1234; 5678; 7812; 3456
=4
Rpta: 16 triángulos

6. 2.-FÓRMULAS PARA CASOS NOTABLES
A. CONTEO DE SEGMENTOS.1
2
3
Fórmula:
#s =
…
n-1
n (n  1)
2
#s = Nº de segmentos
n = # de espacios sobre la línea.
n

7. A. CONTEO DE TRIÁNGULOS
Fórmula:
#t =
1 2 3 …
n
n(n  1)
2
#t = Nº de triángulos
n = # de espacios en la
base

8. A. CONTEO DE CUADRILÁTEROS
i)
1
Fórmula:
2
#c 
3
n(n  1)
2
…
4
#c = Nº de
cuadriláteros
n = #espacios en la
base

9. ii)
m
Fórmula:

2
1
#c 
n(n  1) m (m  1)
2 3 4 … n
n = #casilleros en la base
m = # casilleros sobre un lado
4

10. A.
CONTEO DE CUADRADOS:
i) La figura principal es un cuadrado.1 2 3 4
2
3
4
n
Fórmula:
n
#
S =
n(n  1)(2n  1)
6
La figura debe ser un cuadrado de n x n
n = # de casilleros por lado.

11. ii) La figura principal es un rectángulo
1 2 3
2
m
n
Fórmula:
Nº de cuadrados:
m.n + (m–1)(n-1)+(m-2)(n-2)+…

12. A. CONTEO DE CUBOS Y PARALELEPÍPEDOS
i) Conteo de Cubos (Cubos simples)
Fórmula:
 n(n  1) 
Nºcubos= 

 2 


n
2
1
1 2
n 1
2
2
n = #casilleros por
lado

13. ii) Conteo de Paralelepípedos.
n
2
1
p
1 2
m
1
2
Fórmula:
n(n  1) n(m  1) p(p  1)
Nº de paralelepípedos:
x
x
2
2
2