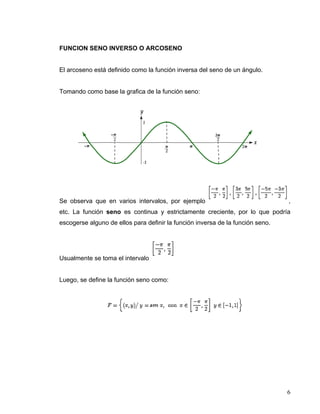
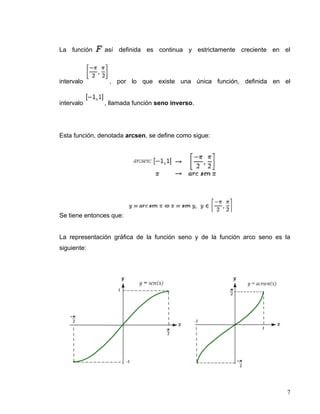
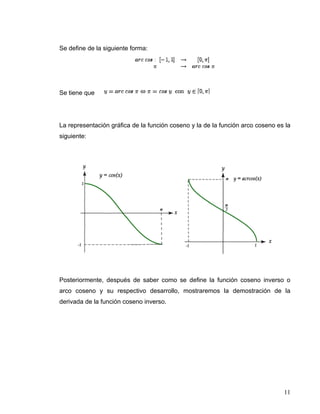
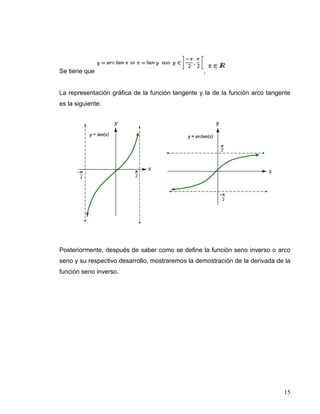
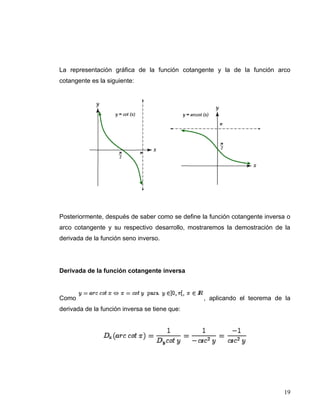
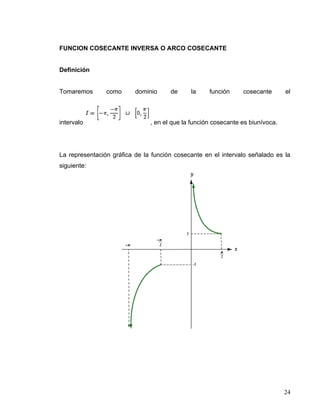
El documento aborda la derivación de funciones trigonométricas inversas, destacando que estas funciones son relaciones que se convierten en funciones al restringir su dominio. Se explican específicamente las funciones seno inverso, coseno inverso, tangente inversa, cotangente inversa, secante inversa y cosecante inversa, junto con sus respectivas derivadas y ejemplos. Además, se enfatiza la continuidad y el comportamiento monótono de estas funciones en sus intervalos definidos.

1. DERIVADA DE LAS FUNCIONES TRIGONOMETRICAS INVERSAS
Para poder derivar las funciones trigonométricas inversas, es necesario tener en
cuenta alguna de los principales aspectos que dará a entender más fácil el
desarrollo de cada una de estas funciones.
• Si una función es continua y estrictamente creciente o decreciente en un
intervalo, entonces posee función inversa la cual también es continua y
estrictamente creciente o decreciente.
• Las funciones trigonométricas son periódicas por lo que la correspondencia
entre la variable independiente y la dependiente no es "uno a uno".
• Tener en cuenta las identidades y ecuaciones trigonométricas.
De aquí se tiene que la inversa de una función trigonométrica no es una función,
es una relación.
Sin embargo, si se restringe el dominio de una función trigonométrica se establece
una relación biunívoca y la inversa de la función trigonométrica sí es una función.
5

2. FUNCION SENO INVERSO O ARCOSENO
El arcoseno está definido como la función inversa del seno de un ángulo.
Tomando como base la grafica de la función seno:
Se observa que en varios intervalos, por ejemplo ,
etc. La función seno es continua y estrictamente creciente, por lo que podría
escogerse alguno de ellos para definir la función inversa de la función seno.
Usualmente se toma el intervalo
Luego, se define la función seno como:
6

3. La función así definida es continua y estrictamente creciente en el
intervalo , por lo que existe una única función, definida en el
intervalo , llamada función seno inverso.
Esta función, denotada arcsen, se define como sigue:
Se tiene entonces que:
La representación gráfica de la función seno y de la función arco seno es la
siguiente:
7

4. Posteriormente, después de saber como se define la función seno inverso o arco
seno y su respectivo desarrollo, mostraremos la demostración de la derivada de la
función seno inverso.
Derivada Del Seno Inverso O Arco Seno
Como aplicando el teorema
de la derivada de una función inversa se tiene que:
Como y entonces
Pues,
Luego:
En general
Como podemos ver, hicimos la demostración de la derivada de la función seno
inverso teniendo en cuenta lo que hemos visto anteriormente sobre función del
seno inverso o arco seno.
8

5. Ejemplos de derivadas trigonométricas inversas (Seno Inverso)



9

6. FUNCION COSENO O ARCO COSENO
El arco coseno es la función inversa del coseno.
• y = arccos x x = cos y; y es el arco cuyo coseno es el ángulo x.
El arco coseno y el coseno son funciones inversas, por tanto su composición
es la función identidad.
• arccos (cos x) = x
Como en la función seno, la función coseno es continua y estrictamente
decreciente en varios intervalos por ejemplo: , etc.
Por lo cual debe restringirse su dominio de tal forma que posea función inversa.
Sea entonces la función tal que:
La función así definida es continua y estrictamente decreciente en el
intervalo , por lo que posee función inversa.
Esta recibe el nombre de arco coseno, (o función coseno inverso), y se
denota .
10

7. Se define de la siguiente forma:
Se tiene que
La representación gráfica de la función coseno y la de la función arco coseno es la
siguiente:
Posteriormente, después de saber como se define la función coseno inverso o
arco coseno y su respectivo desarrollo, mostraremos la demostración de la
derivada de la función coseno inverso.
11

8. Derivada de la función coseno inverso
Como, aplicando el
teorema de la derivada de la función inversa se tiene que:
Como, y entonces
Pues
Luego:
En general
Como podemos ver, hicimos la demostración de la derivada de la función coseno
inverso teniendo en cuenta lo que hemos visto anteriormente sobre función del
coseno inverso o arco coseno.
12

9. Ejemplos de derivadas trigonométricas inversas (Coseno Inverso)
1.
2.
3.

13

10. FUNCION TANGENTE INVERSA O ARCO TANGENTE
El arco tangente es la función inversa de la tangente.
• y = arctg x x = tg y; y es el arco cuya tangente es el ángulo x.
El arco tangente y la tangente son funciones inversas, por tanto su composición es
la función identidad.
• arctg (tg x) = x.
Igual que en los dos casos anteriores, vamos a restringir el dominio de la función
tangente al intervalo , en el que es continua y estrictamente creciente, por
lo que posee función inversa.
Luego se define la función tangente como:
Se define la función tangente inversa, también llamada arco tangente, y
denotada , como:
14

11. Se tiene que ,
La representación gráfica de la función tangente y la de la función arco tangente
es la siguiente:
Posteriormente, después de saber como se define la función seno inverso o arco
seno y su respectivo desarrollo, mostraremos la demostración de la derivada de la
función seno inverso.
15

12. Derivada de la función arco tangente.
Como , aplicando el teorema de la
derivada de la función inversa se tiene que:
Como,
Y
Entonces
Por lo que:
En general
Como podemos ver, hicimos la demostración de la derivada de la función tangente
inverso teniendo en cuenta lo que hemos visto anteriormente sobre función del
tangente inverso o arco tangente.
16

13. Ejemplos de derivadas trigonométricas inversas (Tangente Inverso)
1.
2.
3.


17

14. FUNCION COTANGENTE INVERSA O ARCO COTANGENTE
Para definir la función inversa de la función cotangente, vamos a restringir el
dominio de ésta al intervalo , en el que es continua y estrictamente
decreciente, por lo que posee función inversa.
Se define función cotangente como:
La función cotangente inversa, llamada también arco cotangente y denotada
, se define como:
Por la definición de la función arco cotangente se tiene que
.
Además
18

15. La representación gráfica de la función cotangente y la de la función arco
cotangente es la siguiente:
Posteriormente, después de saber como se define la función cotangente inversa o
arco cotangente y su respectivo desarrollo, mostraremos la demostración de la
derivada de la función seno inverso.
Derivada de la función cotangente inversa
Como , aplicando el teorema de la
derivada de la función inversa se tiene que:
19

16. Como,
Y
Entonces
Por lo que:
En general
Como podemos ver, hicimos la demostración de la derivada de la función
cotangente inversa teniendo en cuenta lo que hemos visto anteriormente sobre
función de la cotangente inversa o arco cotangente.
Ejemplos de derivadas trigonométricas inversas (Cotangente Inverso)
20

17. FUNCION SECANTE INVERSO O ARCO SECANTE
Definición
En la función secante, es necesario elegir como dominio de la función secante el
intervalo de donde , ya que en la función secante es
biunívoca y la derivada de la función inversa puede expresarse por medio de una
sola fórmula.
La representación gráfica de la función secante en el intervalo señalado es el
siguiente:
Como puede observarse, la función secante es continua en , siendo
estrictamente decreciente en y estrictamente creciente en .
Existe por tanto la función secante inversa, llamada también arco secante y se
denota definida por:
21

18. Por la definición de función arco secante se tiene que:
Posteriormente, después de saber como se define la función secante inversa o
arco secante y su respectivo desarrollo, mostraremos la demostración de la
derivada de la función seno inverso.
Derivada de la función secante inversa
Como ,
utilizando el teorema de la derivada de la función inversa se obtiene que:
Como,
Y
Cuando,
22

19. Entonces
Pues
Luego
En general, si
Entonces
Como podemos ver, hicimos la demostración de la derivada de la función secante
inversa teniendo en cuenta lo que hemos visto anteriormente sobre función de la
secante inversa o arco secante.
Ejemplos de derivadas trigonométricas inversas (Secante Inversa)
23

20. FUNCION COSECANTE INVERSA O ARCO COSECANTE
Definición
Tomaremos como dominio de la función cosecante el
intervalo , en el que la función cosecante es biunívoca.
La representación gráfica de la función cosecante en el intervalo señalado es la
siguiente:
24

21. Como puede observarse, la función cosecante es continua en , siendo
estrictamente creciente en y estrictamente decreciente en .
Existe por tanto la función cosecante inversa, llamada también arco cosecante y
que se denota definida por:
Por la definición de función arco cosecante se tiene que:
La representación gráfica de la función arco cosecante es la siguiente:
25

22. Posteriormente, después de saber como se define la función cosecante inversa o
arco cosecante y su respectivo desarrollo, mostraremos la demostración de la
derivada de la función seno inverso.
Derivada de la función cosecante inversa
Como ,
utilizando el teorema de la derivada de la función inversa se obtiene que:
Como,
Y, Para
Entonces
Pues
Luego
En general, si entonces
Como podemos ver, hicimos la demostración de la derivada de la función
cosecante inversa teniendo en cuenta lo que hemos visto anteriormente sobre
función de la cosecante inversa o arco cosecante.
26

23. Ejemplos de derivadas trigonométricas inversas (Cosecante Inversa)
27