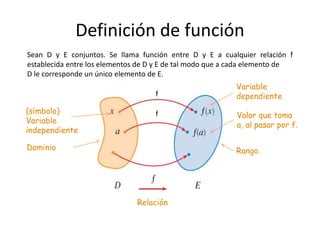
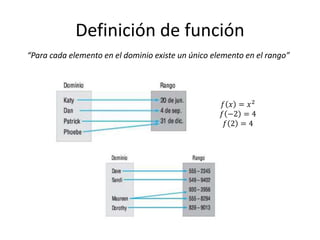
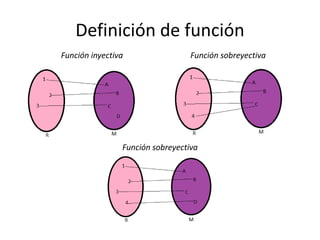
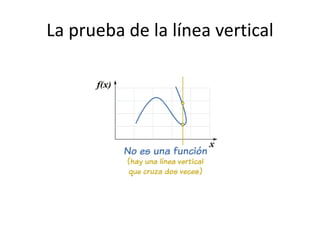
El documento resume brevemente la historia del concepto de función desde Galileo Galilei hasta Edouard Goursat. Galilei entendió la relación entre variables, Descartes representó relaciones entre magnitudes mediante ecuaciones y curvas, y Johann Bernoulli introdujo por primera vez el término "función". Posteriormente, Euler y Goursat dieron definiciones más formales de función que se usan hoy en día.

1. Funciones
Definición de función

2. Breve historia de las funciones
Galileo Galilei (1564-1642)
Pareció entender el concepto de función aún con mayor claridad. Sus estudios
sobre el movimiento contienen la clara comprensión de una relación entre
variables.

3. Breve historia de las funciones
René Descartes (1596-1650)
Descartes desarrolló y llevó a sus fundamentales consecuencias las ideas que
siglos atrás se habían usado para representar en el plano relaciones entre
magnitudes. Ahora cualquier curva del plano podía ser expresada en términos de
ecuaciones y cualquier ecuación que relacionara dos variables podía ser
representada geométricamente en un plano.

4. Breve historia de las funciones
Johann Bernoulli (1667-1748)  no es el mimo que Daniel Bernoulli
A finales del siglo XVII aparece por primera vez el término función. En palabras de
Johann Bernoulli, una función es
“una cantidad formada de alguna manera a partir de cantidades indeterminadas
y constantes”.

5. Breve historia de las funciones
Leonhard Euler (1707-1783)
1748 Introducción al análisis infinito:
“Una función de una cantidad variable es una expresión analítica compuesta de
cualquier manera a partir de la cantidad variable y de números o cantidades
constantes.”

6. Breve historia de las funciones
Leonhard Euler (1707-1783)
1755
“Si algunas cantidades dependen de otras del tal modo que si estas últimas
cambian también lo hacen las primeras, entonces las primeras cantidades se
llaman funciones de las segundas.”

7. Breve historia de las funciones
Édouard Jean-Baptiste Goursat (1858 – 1936)
Edouard Goursat dio en 1923 la definición que aparece en la mayoría de los libros
de textos hoy en día:
“Se dice que y es una función de x si a cada valor de x le
corresponde un único valor de y. Esta correspondencia se
indica mediante la ecuación: y=ƒ(x)”

8. Definición de función
Sean D y E conjuntos. Se llama función entre D y E a cualquier relación f
establecida entre los elementos de D y E de tal modo que a cada elemento de
D le corresponde un único elemento de E.
Dominio
f
f
Relación
Variable
dependiente
Valor que toma
a, al pasar por f.
Rango.
(símbolo)
Variable
independiente

9. Definición de función
“Para cada elemento en el dominio existe un único elemento en el rango”
𝑓 𝑥 = 𝑥2
𝑓 −2 = 4
𝑓 2 = 4

10. Definición de función
“Para cada elemento en el dominio existe un único elemento en el rango”
Tenemos los pares {(1,2),(1,-2),(2,3),(3,4)}. ¿Es una función?
¿Estas relaciones serían funciones? {(5,10),(10,10),(5,10)}

11. Definición de función
Función inyectiva Función sobreyectiva
Función sobreyectiva

12. La prueba de la línea vertical

13. Notación
Se designa f a una función de A en B esto se escribe simbólicamente por:
𝑓𝐴 → 𝐵 𝑜 𝐴 →
𝑓
𝐵
Se llama imagen f(x) al elemento de llegada en B asociada por f del elemento x del
conjunto A.
𝑥 → 𝑓 𝑥 𝑜 𝑥 → 𝑦 = 𝑓(𝑥)
Ejemplo 1:
La función f que determina el tiempo para viajar en auto entre dos ciudades quedaría
definida por:
𝑓: 𝐴 → 𝐵
𝑥 → 𝑇 = 𝑓 𝑥
Donde A es el conjunto del cuál se tomarán los valores para x de tal forma que al ser
reemplazados en la fórmula T=f(x) sea posible determinar el tiempo de viaje T.

14. Notación