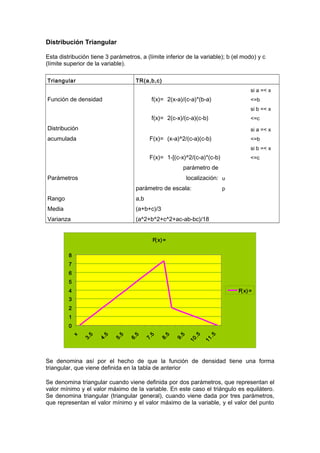
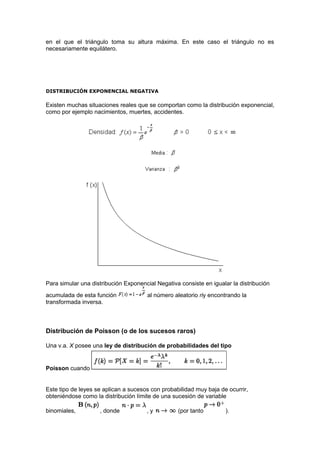
La distribución triangular tiene 3 parámetros (a, b, c) que representan el límite inferior, el modo y el límite superior. La función de densidad y distribución acumulada asumen diferentes formas dependiendo de si el valor está entre a y b, o entre b y c. La media es (a+b+c)/3 y la varianza depende de los parámetros.

1. Distribución Triangular
Esta distribución tiene 3 parámetros, a (límite inferior de la variable); b (el modo) y c
(límite superior de la variable).
Triangular TR(a,b,c)
Función de densidad f(x)= 2(x-a)/(c-a)*(b-a)
si a =< x
<=b
f(x)= 2(c-x)/(c-a)(c-b)
si b =< x
<=c
Distribución
acumulada F(x)= (x-a)^2/(c-a)(c-b)
si a =< x
<=b
F(x)= 1-[(c-x)^2/(c-a)*(c-b)
si b =< x
<=c
Parámetros
parámetro de
localización: u
parámetro de escala: p
Rango a,b
Media (a+b+c)/3
Varianza (a^2+b^2+c^2+ac-ab-bc)/18
F( x)=
8
7
6
5
4
3
2
1
0
x
3.5
4.5
5.5
6.5
7.5
8.5
9.5
10 .5
11 .5
F( x)=
Se denomina así por el hecho de que la función de densidad tiene una forma
triangular, que viene definida en la tabla de anterior
Se denomina triangular cuando viene definida por dos parámetros, que representan el
valor mínimo y el valor máximo de la variable. En este caso el triángulo es equilátero.
Se denomina triangular (triangular general), cuando viene dada por tres parámetros,
que representan el valor mínimo y el valor máximo de la variable, y el valor del punto

2. en el que el triángulo toma su altura máxima. En este caso el triángulo no es
necesariamente equilátero.
DISTRIBUCIÓN EXPONENCIAL NEGATIVA
Existen muchas situaciones reales que se comportan como la distribución exponencial,
como por ejemplo nacimientos, muertes, accidentes.
Para simular una distribución Exponencial Negativa consiste en igualar la distribución
acumulada de esta función al número aleatorio riy encontrando la
transformada inversa.
Distribución de Poisson (o de los sucesos raros)
Una v.a. X posee una ley de distribución de probabilidades del tipo
Poisson cuando
Este tipo de leyes se aplican a sucesos con probabilidad muy baja de ocurrir,
obteniéndose como la distribución límite de una sucesión de variable
binomiales, , donde , y (por tanto ).

3. La demostración de esto consiste en
En general utilizaremos la distribución de Poisson como aproximación de
experimentos binomiales donde el número de pruebas es muy alto, pero la
probabilidad de éxito muy baja. A veces se suele utilizar como criterio de
aproximación:
La ley de Poisson la podemos encontrar tabulada en la tabla número 2, para ciertos
valores usuales de .
La función característica de es
de lo que se deduce que valor esperado y varianza coinciden