Este documento describe diferentes distribuciones de probabilidad, incluyendo la distribución binomial, Poisson y normal. Explica que al finalizar el curso, los estudiantes aprenderán a calcular probabilidades asociadas con estas distribuciones y aplicar herramientas estadísticas para la toma de decisiones empresariales. Se enfoca en particular en la distribución normal, describiendo sus propiedades clave y cómo modela muchos fenómenos naturales.

2.  Al finalizar el curso, el alumno aplica herramientas estadísticas
para la toma de decisiones tácticas en el ámbito empresarial.
LOGRO DEL CURSO:

3. Logro:
 Al finalizar la unidad el alumno calcula probabilidades asociadas a una variable
aleatoria que se distribuye Binomialmente, por Poisson o Normalmente
DISTRIBUCIONES DE PROBABILIDAD

4. DISTRIBUCIÓN DE PROBABILIDAD CONTINUA:
DISTRIBUCIÓN NORMAL
 En estadística y probabilidad se
llama distribución normal,
distribución de Gauss o
distribución gaussiana, a una de
las distribuciones de probabilidad
de variable continua que con
más frecuencia aparece
aproximada en fenómenos
reales.

5. La gráfica de su función de densidad tiene una forma acampanada y
es simétrica respecto de un determinado parámetro.
Esta curva se conoce como campana de gauss.

6. DISTRIBUCIÓN DE PROBABILIDAD CONTINUA:
DISTRIBUCIÓN NORMAL
 Algunos ejemplos de variables asociadas a
fenómenos naturales que siguen el modelo de la
normal son:
 Caracteres morfológicos de individuos como la
estatura;
 Caracteres fisiológicos como el efecto de un fármaco;
 Caracteres sociológicos como el consumo de cierto
producto por un mismo grupo de individuos;
 Caracteres psicológicos como el cociente intelectual;
 nivel de ruido en telecomunicaciones;
 errores cometidos al medir ciertas magnitudes; etc.

7. Se dice que una variable aleatoria continua X sigue una distribución normal de parámetros μ y σ y se denota
x~n(μ, σ) si su función de densidad está dada por:
Función de densidad:

8. Se llama distribución normal "estándar" a aquélla en la
que sus parámetros toman los valores μ = 0 y σ = 1.

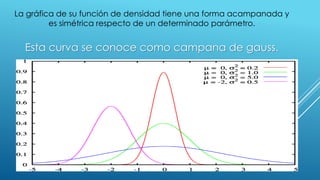
9.  Es simétrica respecto de su media, μ;
 Distribución de probabilidad alrededor de la media en una distribución N(μ, σ).La moda
y la mediana son ambas iguales a la media, μ;
 Los puntos de inflexión de la curva se dan para x = μ − σ y x = μ + σ.
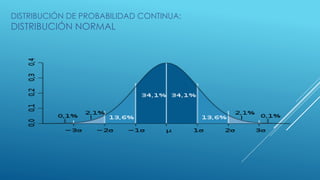
 Distribución de probabilidad en un entorno de la media:
 En el intervalo [μ - σ, μ + σ] se encuentra comprendida, aproximadamente, el 68,26% de
la distribución;
 En el intervalo [μ - 2σ, μ + 2σ] se encuentra, aproximadamente, el 95,44% de la
distribución;
 Por su parte, en el intervalo [μ -3σ, μ + 3σ] se encuentra comprendida,
aproximadamente, el 99,74% de la distribución. Estas propiedades son de gran utilidad
para el establecimiento de intervalos de confianza. Por otra parte, el hecho de que
prácticamente la totalidad de la distribución se encuentre a tres desviaciones típicas de
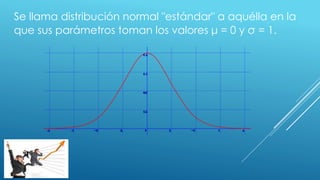
la media justifica los límites de las tablas empleadas habitualmente en la normal
estándar
ALGUNAS PROPIEDADES DE LA DISTRIBUCIÓN NORMAL SON:

10. DISTRIBUCIÓN DE PROBABILIDAD CONTINUA:
DISTRIBUCIÓN NORMAL

11. Estandarización de variables aleatorias normales como consecuencia de la propiedad 1; es posible
relacionar todas las variables aleatorias normales con la distribución normal estándar.
SI X se distribuye normalmente: