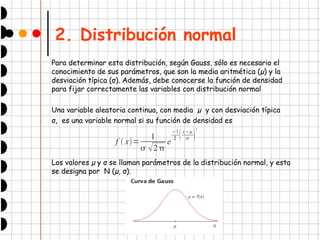
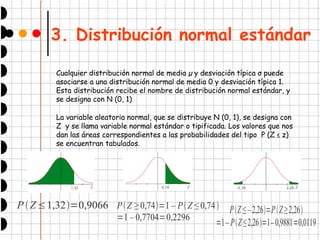
Este documento trata sobre las distribuciones continuas y la distribución normal. Explica que las distribuciones continuas se estudian de forma análoga a las discretas mediante funciones de densidad. Luego describe la distribución normal, indicando que depende de dos parámetros, la media y la desviación típica. También introduce la distribución normal estándar y cómo tipificar variables para trabajar con esta distribución patrón. Por último, explica cómo la distribución binomial se puede aproximar a la normal cuando el número de ensayos es grande.

1. Tema 11
Distribución continuas.
Distribución Normal

2. Índice
➢
Distribuciones estadísticas continuas
➢
Distribuciones de probabilidad continuas
➢
Distribución normal o de Gauss
➢
Distribución normal estándar
➢
Tipificación de la variable
➢
La distribución binomial se aproxima a la normal

3. 1. Distribuciones
estadísticas continuas
Las distribuciones estadísticas correspondientes a las variables
estadísticas continuas se estudian de forma análoga a las de las
variables estadísticas discretas.
Fácilmente podemos observar que el
área encerrada por todos los rectángulos
es la suma de las frecuencias relativas,
es decir, la unidad.
Si el proceso de ir acortando la longitud
de los intervalos se repite indefinidamente,
los polígonos de frecuencias correspondien-
tes tienden a una línea curva continua que
llamaremos función de densidad o función
de probabilidad.
Pa≤X ≤b=area coloreada

4. Distribuciones de
probabilidad continuas
➢La función de densidad o función de probabilidad de una variable
continua X, es la función que nos permite, en las distribuciones
continuas, hallar probabilidades mediante el cálculo de áreas.
➢La distribución de probabilidad asociada a una variable aleatoria
continua se llama distribución de probabilidad continua.
➢En una distribución continua la probabilidad de un valor concreto es
cero.
➢En este caso, las probabilidades que calculamos están siempre
asociadas a intervalos:
La función de densidad o función de probabilidad de una variable
continua X, es la función que nos permite, en las distribuciones
continuas, hallar probabilidades mediante el cálculo de áreas.
Pa≤X≤b

5. 1.1 Propiedades de la
función de densidad
La función de densidad, , ha de ser definida positiva.
El área comprendida entre la gráfica de la función de densidad y el eje
OX vale 1, puesto que es la probabilidad de que la variable aleatoria
tome cualquier valor.
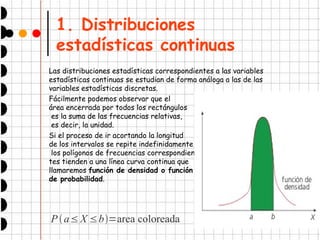
La probabilidad de que la variable aleatoria tome
un valor en el intervalo [a, b ] es el área del recin-
to limitado por la gráfica entre la función de den-
sidad, el eje OX y las rectas x = a y x = b.
f  x f  x≥0
Pa≤X ≤b=área del recinto coloreado

6. 2. Distribución normal
Para determinar esta distribución, según Gauss, sólo es necesario el
conocimiento de sus parámetros, que son la media aritmética (µ) y la
desviación típica (σ). Además, debe conocerse la función de densidad
para fijar correctamente las variables con distribución normal
Una variable aleatoria continua, con media µ y con desviación típica
σ, es una variable normal si su función de densidad es
Los valores µ y σ se llaman parámetros de la distribución normal, y esta
se designa por N (µ, σ).
f  x=
1
 2
e
−1
2 x−
 
2

7. 2. 1 Propiedades de la
distribución normal
Dominio: toda la recta real. Hay que hacer notar que, para valores superiores a 4
o inferiores a –4, los valores que toma la función son poco significativos.
Simetría: la función es simétrica respecto de la recta vertical x = µ, ya que se
cumple para cualquier número real a, f (µ + a) = f (µ – a).
Cortes con los ejes: con el eje de abscisas, OX, no presenta cortes; con el eje
de ordenadas, OY, tiene un corte en el punto de coordenadas
La función posee un máximo en el punto de abscisa x = µ.
Monotonía: la función es creciente hasta la recta x = µ y decreciente desde esta
recta en adelante.
Puntos de inflexión: la función posee dos puntos de inflexión, situados en los
valores de las abscisas x = µ – σ y x = µ + σ.
Área encerrada bajo la curva: el área comprendida entre la curva y el eje de
abscisas vale la unidad.
0 ,
e
−

2
2
2
 2 

8. 3. Distribución normal estándar
Cualquier distribución normal de media µ y desviación típica σ puede
asociarse a una distribución normal de media 0 y desviación típica 1.
Esta distribución recibe el nombre de distribución normal estándar, y
se designa con N (0, 1).
La variable aleatoria normal, que se distribuye N (0, 1), se designa con
Z y se llama variable normal estándar o tipificada. Los valores que nos
dan las áreas correspondientes a las probabilidades del tipo P (Z ≤ z)
se encuentran tabulados.
PZ≤1,32=0,9066 PZ ≥ 0,74=1 – PZ ≤ 0,74
=1 – 0,7704=0,2296
PZ ≤ –2,26=PZ≥2,26
=1– PZ≤2,26=1–0,9881=0,0119

9. 4. Tipificación de la variable
En las situaciones prácticas, las distribuciones normales no suelen
coincidir con la normal de media µ = 0 y desviación típica σ = 1. Por
tanto, es aconsejable transformar la variable problema en la variable
estándar que sigue la distribución N (0, 1).
Se denomina tipificación de la variable al paso de la variable X que
sigue una distribución N (µ, σ) a otra variable Z que sigue la
distribución N (0, 1). Esta transformación consiste en:
Trasladar, es decir, hacer la media cero (µ = 0).
Reducir, o sea, hacer la desviación típica uno (σ = 1).
Las dos transformaciones anteriores se consiguen
realizar a la vez, sin más que hacer el cambio de variable:
Los valores que se distribuyen según la normal N (0, 1)
y que designamos con la variable Z reciben el nombre de puntuaciones
tipificadas.
Z =
X – µ


10. 5. La distribución binomial
se aproxima a la normal
El matemático Abraham de Moivre (1667-1754) demostró, que bajo ciertas
condiciones, se puede obtener una buena aproximación de la distribución
binomial mediante una distribución normal.
Si X es una variable aleatoria discreta que sigue una distribución binomial
de parámetros n y p, entonces se aproxima a una variable normal
La aproximación es tanto mejor cuanto mayor sea n y cuanto más próximo
está p de 0,5, en general sera una buena aproximación si
Corrección de continuidad o de Yates
Cuando aproximamos una distribución binomial mediante una normal, estamos
convirtiendo una variable X discreta en otra continua.
Los valores de la probabilidad para valores fijos de la variable continua son
cero. Para evitar este problema en la aproximación de los valores fijos,
estos se corrigen sustituyéndolos por un intervalo centrado en el valor de la
variable y de amplitud la unidad.
N np ,npq
n⋅p≥5

11. 5.1 La distribución binomial
se aproxima a la normal
En el siguiente recuadro podemos ver todas las situaciones posibles: