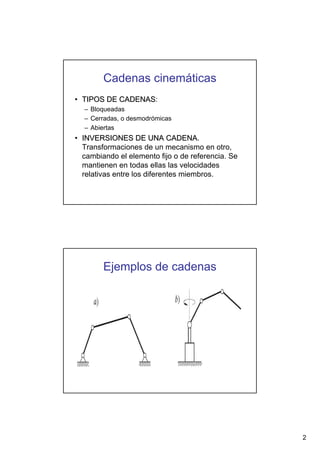
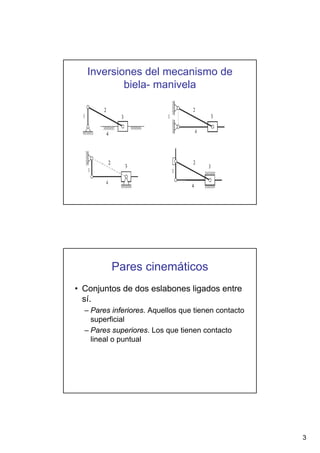
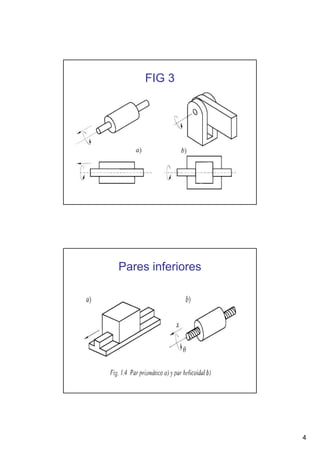
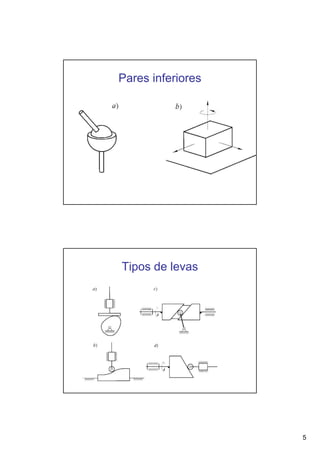
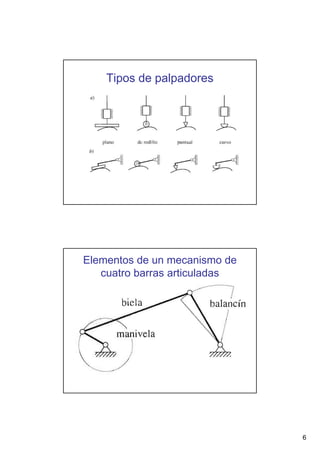
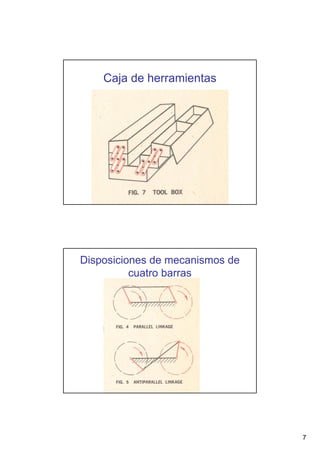
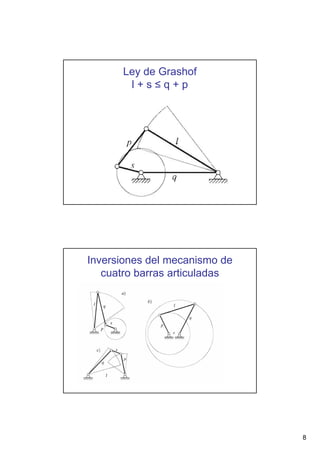
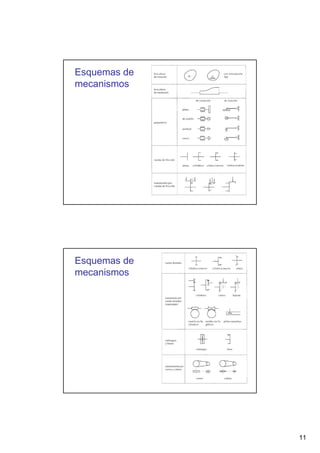
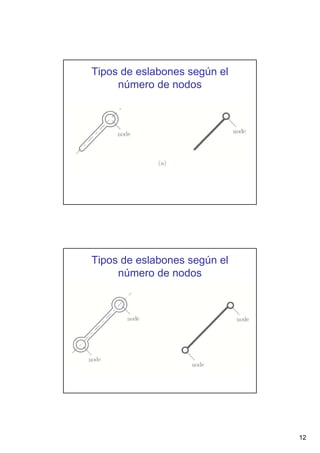
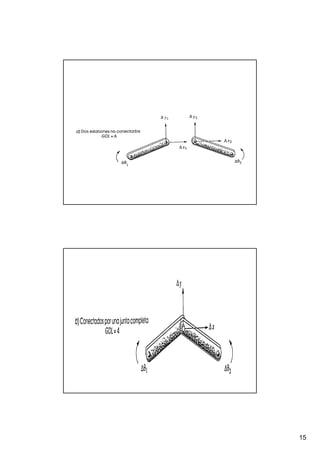
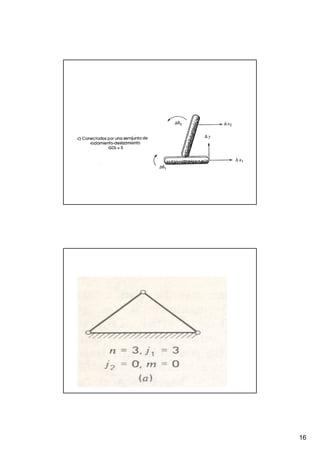
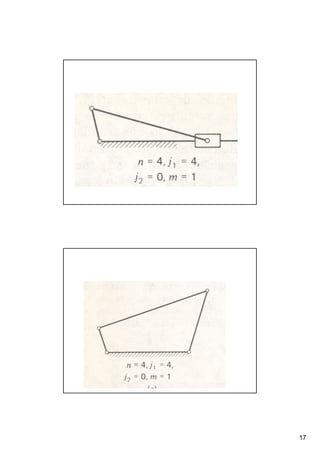
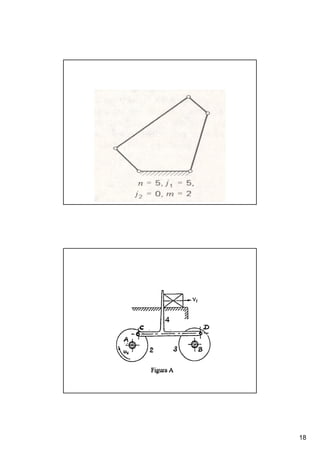
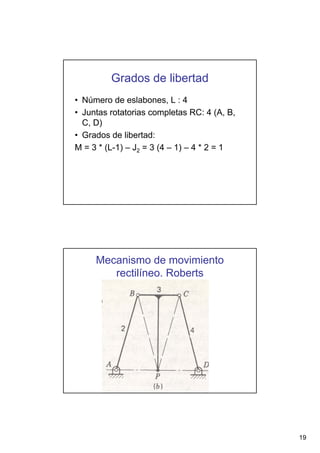
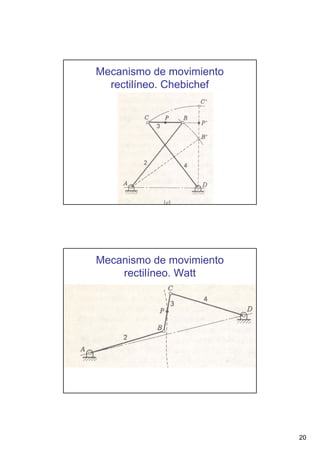
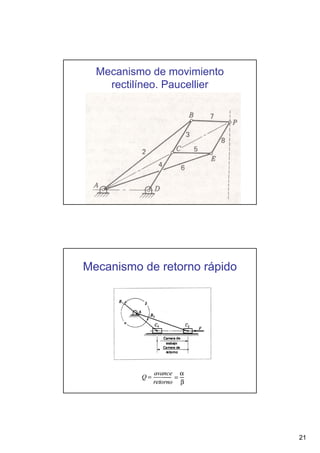
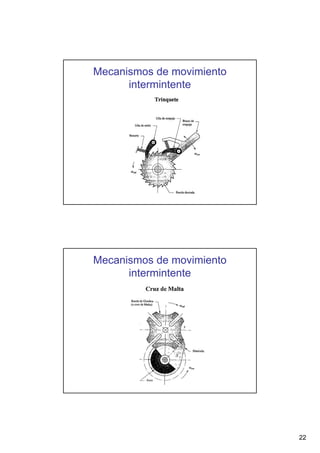
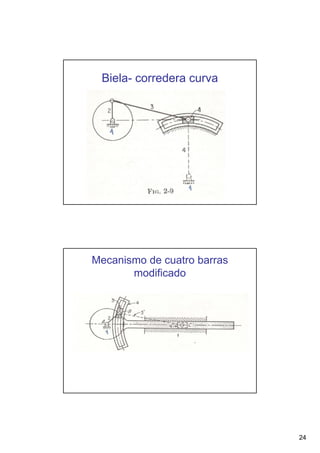
Este documento presenta conceptos básicos sobre sistemas mecánicos y mecanismos. Define términos como miembro, cadena cinemática y eslabón. Explica tipos de cadenas como bloqueadas, cerradas y abiertas, e introduce conceptos como inversiones de cadenas y pares cinemáticos. Finalmente, cubre temas como mecanismos planos, grados de libertad, coordenadas generalizadas y varios ejemplos de mecanismos como el mecanismo de biela-manivela y el mecanismo

1. Asignatura de Sistemas
Mecánicos
MECANISMOS 1
Algunas definiciones
• MIEMBRO. Elemento material de una
MIEMBRO
máquina o mecanismo, que puede ser
sólido rígido, sólido deformable o fluido.
• CADENA CINEMÁTICA. Conjunto o
TICA
subconjunto de miembros de un
mecanismo que están enlazados entre sí.
• ESLABÓN. Cada uno de los miembros de
una cadena cinemática.
1

2. Cadenas cinemáticas
• TIPOS DE CADENAS:
CADENAS
– Bloqueadas
– Cerradas, o desmodrómicas
– Abiertas
• INVERSIONES DE UNA CADENA.
CADENA
Transformaciones de un mecanismo en otro,
cambiando el elemento fijo o de referencia. Se
mantienen en todas ellas las velocidades
relativas entre los diferentes miembros.
Ejemplos de cadenas
2

3. Inversiones del mecanismo de
biela- manivela
Pares cinemáticos
• Conjuntos de dos eslabones ligados entre
sí.
– Pares inferiores. Aquellos que tienen contacto
superficial
– Pares superiores. Los que tienen contacto
lineal o puntual
3

4. FIG 3
Pares inferiores
4

5. Pares inferiores
Tipos de levas
5

6. Tipos de palpadores
Elementos de un mecanismo de
cuatro barras articuladas
6

7. Caja de herramientas
Disposiciones de mecanismos de
cuatro barras
7

8. Ley de Grashof
l+s≤q+p
Inversiones del mecanismo de
cuatro barras articuladas
8

9. Esquemas de elementos de
mecanismos
Mecanismos planos
• Son aquellos cuyos diferentes puntos se
mueven en un mismo plano o en planos
paralelos entre sí.
• MECANISMOS ARTICULADOS. Están
formados por bielas, manivelas y palancas, con
pares giratorios o deslizantes
• Permiten convertir:
– Rotación continua en rotación continua
– Rotación continua en movimiento oscilatorio o
alternativo
– Movimiento oscilatorio en otro oscilatorio
– Movimiento oscilatorio en otro alternativo.
9

10. Esquemas de elementos de
mecanismos
Esquemas
de pares
10

11. Esquemas de
mecanismos
Esquemas de
mecanismos
11

12. Tipos de eslabones según el
número de nodos
Tipos de eslabones según el
número de nodos
12

13. Tipos de eslabones según el
número de nodos
Movilidad
• COORDENADAS INDEPENDIENTES. Es el
número mínimo de variables indpendientes
para describir la configuración de un
mecanismo.
• GRADOS DE LIBERTAD. Es el número mínimo
de variables necesarias para describir la
distribución de velocidades.
• ECUACIONES DE ENLACE. Son las que
pueden establecerse entre diferentes
elementos, cuando se emplea un conjunto no
mínimo en la descripción del mecanismo.
13

14. Coordenadas generalizadas
• Son las variables geométricas de posición y orientación
empleadas para describir las posibles configuraciones
de un sistema mecánico.
• Se intenta que estén asociadas a distancias y ángulos
fácilmente identificables.
• Atendiendo a su referencia, pueden ser
– Absolutas
– Relativas
• Según el tipo de relación, son
– Cartesianas
– Polares, …
Grados de libertad de
mecanismos planos
CRITERIO DE GRÜBLER-KUTZBACH
M = 3 (n – 1) - 2j1 – j2
donde:
– M: grados de libertad.
– n: número de elementos (eslabones, barras, piezas,
etc.) de un mecanismo.
– j1 : número de uniones de 1 grado de libertad.
– j2 : número de uniones de 2 grados de libertad.
14

15. 15

16. 16

17. 17

18. 18

19. Grados de libertad
• Número de eslabones, L : 4
• Juntas rotatorias completas RC: 4 (A, B,
C, D)
• Grados de libertad:
M = 3 * (L-1) – J2 = 3 (4 – 1) – 4 * 2 = 1
Mecanismo de movimiento
rectilíneo. Roberts
19

20. Mecanismo de movimiento
rectilíneo. Chebichef
Mecanismo de movimiento
rectilíneo. Watt
20

21. Mecanismo de movimiento
rectilíneo. Paucellier
Mecanismo de retorno rápido
21

22. Mecanismos de movimiento
intermintente
Mecanismos de movimiento
intermintente
22

23. Mecanismo de biela- manivela
Análisis de posiciones.
Mecanismo de biela- manivela
que se puede escribir aproximadamente como
23

24. Biela- corredera curva
Mecanismo de cuatro barras
modificado
24

25. Yugo escocés
Análisis cinemático del yugo
escocés
25

26. Mecanismos articulados isósceles.
Elipsógrafo
Análisis de posiciones.
Elipsógrafo
26

27. Análisis de posiciones del
mecanismo de cuatro barras
Planteamiento del problema
27

28. Ecuación de Freudenstein
28

29. Palancas rodantes
BIBLIOGRAFÍA DE SISTEMAS
MECÁNICOS
Introducción
ANÓNIMO, How Things Work. Paladin, London (1975), 2 Vols.
ARTOBOLEVSKI, I.I., Mecanismos en la Técnica Moderna. Mir, Moscú
(1979).
ASIMOV, I., Enciclopedia Biográfica de Ciencia y Tecnología. Alianza,
Madrid (1987) 4 vols.
CALERO, R. y CARTA, J.A., Fundamentos de Mecanismos y
Máquinas para Ingenieros. McGraw- Hill, Madrid (1999).
CARDONA, S. y CLOS, D., Teoría de Máquinas. Ediciones UPC,
Barcelona (2001).
ERDMAN, A.G. y SANDOR, G.N. Diseño de Mecanismos. Análisis y
Síntesis. Prentice Hall, México (1998) 3ª Ed.
29

30. HAM, C.W., CRANEE.J. y ROGERS, W.L., Mecanismos.
Ediciones del Castillo, Madrid (1971).
HISCOX, G.D., 1800 Mechanical Movements, Devices and
Appliances. Dover, Mineola, NJ (2007). 1st Ed. 1921.
KOZHEVNIKOV, S.N., Mecanismos. Gustavo Gili,
Barcelona (1975).
NORTON, R.L., Diseño de Maquinaria. McGraw- Hil
Interamericana, México (2005), 3ª Ed.
PEDRETTI, C. Leonardo. The Machines. Giunti, Florence
(2000).
SCHWAMB, P. et al., Nociones de Mecanismos. Aguilar,
Madrid (1962).
30