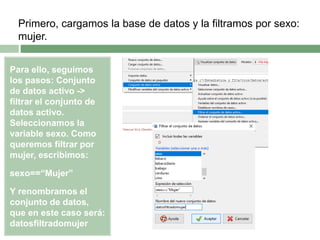
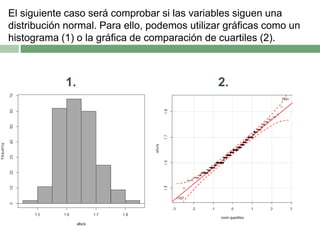
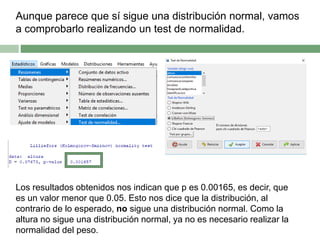
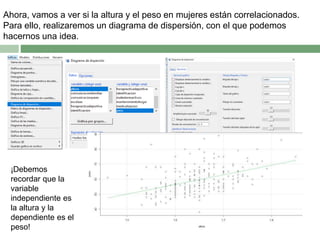
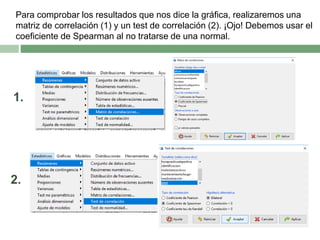
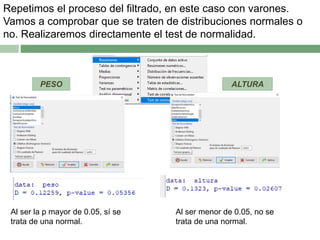
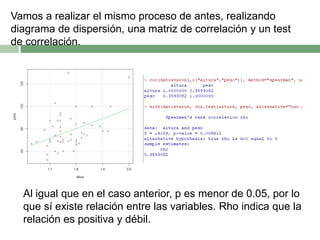
Este documento describe el proceso de correlacionar la altura y el peso diferenciando por sexo. Primero se filtran los datos por mujeres, y se determina que la altura no sigue una distribución normal mientras que el peso sí. Luego, se muestra que existe una correlación débil pero positiva entre la altura y el peso en mujeres. El mismo proceso se repite para los hombres, encontrando también una correlación débil y positiva entre la altura y el peso.

1. TAREA 8
Soledad Pérez Sánchez GRUPO 1,
SUBGRUPO 5
Realizar la correlación entre peso y altura,
pero diferenciando por sexo. Es decir:
-altura y peso en mujeres
-altura y peso en hombre

2. Correlación de altura y peso en mujeres
PRIMERA PARTE

3. Para ello, seguimos
los pasos: Conjunto
de datos activo ->
filtrar el conjunto de
datos activo.
Seleccionamos la
variable sexo. Como
queremos filtrar por
mujer, escribimos:
sexo==“Mujer”
Y renombramos el
conjunto de datos,
que en este caso será:
datosfiltradomujer
Primero, cargamos la base de datos y la filtramos por sexo:
mujer.

4. El siguiente caso será comprobar si las variables siguen una
distribución normal. Para ello, podemos utilizar gráficas como un
histograma (1) o la gráfica de comparación de cuartiles (2).
1. 2.

5. Aunque parece que sí sigue una distribución normal, vamos
a comprobarlo realizando un test de normalidad.
Los resultados obtenidos nos indican que p es 0.00165, es decir, que
es un valor menor que 0.05. Esto nos dice que la distribución, al
contrario de lo esperado, no sigue una distribución normal. Como la
altura no sigue una distribución normal, ya no es necesario realizar la
normalidad del peso.

6. Ahora, vamos a ver si la altura y el peso en mujeres están correlacionados.
Para ello, realizaremos un diagrama de dispersión, con el que podemos
hacernos una idea.
¡Debemos
recordar que la
variable
independiente es
la altura y la
dependiente es el
peso!

7. Para comprobar los resultados que nos dice la gráfica, realizaremos una
matriz de correlación (1) y un test de correlación (2). ¡Ojo! Debemos usar el
coeficiente de Spearman al no tratarse de una normal.
1.
2.

8. Los resultados obtenidos son los siguientes:
-El valor de p es muy pequeño, menor que
0.05, lo que significa que se debe rechazar
la hipótesis nula, y se acepta la alternativa:
la altura si influye en el peso.
-Además, rho indica que la relación es débil,
aunque no mucho, pues es un valor cercano
a 0.5.

9. Correlación de altura y peso en hombres
Segunda parte

10. Repetimos el proceso del filtrado, en este caso con varones.
Vamos a comprobar que se traten de distribuciones normales o
no. Realizaremos directamente el test de normalidad.
Al ser la p mayor de 0.05, sí se
trata de una normal.
Al ser menor de 0.05, no se
trata de una normal.
PESO ALTURA

11. Vamos a realizar el mismo proceso de antes, realizando
diagrama de dispersión, una matriz de correlación y un test
de correlación.
Al igual que en el caso anterior, p es menor de 0.05, por lo
que sí existe relación entre las variables. Rho indica que la
relación es positiva y débil.

12. ¡Gracias por su atención!
FIN