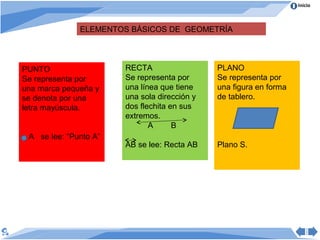
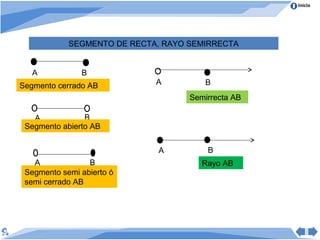
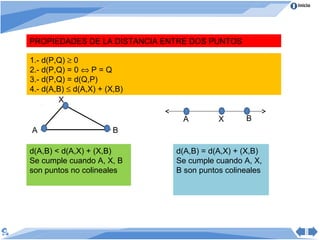
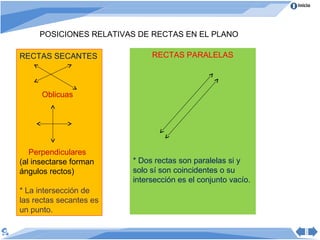
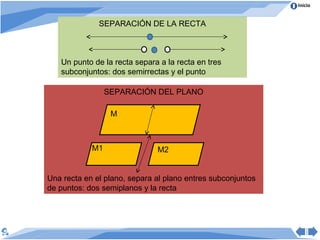
Este documento presenta conceptos básicos de geometría. Define geometría como el estudio de las propiedades de figuras geométricas como puntos, rectas, ángulos, polígonos y círculos. Explica elementos básicos como puntos, rectas, segmentos de recta, semirrectas y rayos. También cubre proposiciones matemáticas como axiomas, postulados y teoremas, y propiedades de la distancia entre puntos y posiciones relativas de rectas.

1. Presentación
Contenido Temático
Recursos
ELEMENTOS BÁSICOS DE
Evaluación GEOMETRÍA
Prof. Gustavo Adolfo Bojorquez Márquez
Bibliografía
MATEMÁTICA
Créditos 3ro de Secundaria

2. Inicio

3. Inicio
Presentación
La Geometría existe en todas partes (palabras atribuidas a Platón). Procure
mirar las formas regulares y perfectas que presentan algunos cuerpos. Las
flores, las hojas y muchos animales revelan simetrías admirables que
deslumbran nuestro espíritu. La geometría repito existe en todas partes. En el
disco del Sol, en la hoja del datilero, en el arco iris, en la mariposa, en el
diamante, en la estrella del mar y hasta en un pequeño grano de arena. Hay,
en fin, infinita variedad de formas geométricas presentadas por la
naturaleza…….La geometría existe, como dijo el gran filósofo, en todas partes.
Sin embargo, es preciso saber verla, tener inteligencia para comprenderla y
alma para admirarla………..Dios fue un gran geómetra. Geometrizó la tierra y el
Cielo (frase de Platón).
Estracto del libro “El Hombre que Calculaba”

4. Inicio
DEFINICIÓN DE GEOMETRÍA
La geometría trata del estudio de las propiedades de las figuras
geométricas: puntos, rectas, ángulos, polígonos,circunferencias y
sólidos. De la medición y relaciones que guardan entre sí

5. Inicio
ELEMENTOS BÁSICOS DE GEOMETRÍA
PUNTO RECTA PLANO
Se representa por Se representa por Se representa por
una marca pequeña y una línea que tiene una figura en forma
se denota por una una sola dirección y de tablero.
letra mayúscula. dos flechita en sus
sssss
extremos.
A B
A se lee: “Punto A”
AB se lee: Recta AB Plano S.

6. Inicio
SEGMENTO DE RECTA, RAYO SEMIRRECTA
A B
Segmento cerrado AB A B
Semirrecta AB
A B
Segmento abierto AB
A B
A B Rayo AB
Segmento semi abierto ó
semi cerrado AB

7. Inicio
PROPOSICIONES MATEMÁTICAS
AXIOMA.- Es una proposición evidente por sí misma y aceptada por el
sentido común sin necesidad de demostrarla. Los axiomas tratan de la
matemática en general.
Ejemplo: “El todo es mayor que cualquier de las partes”
POSTULADO.- Es también una proposición que se acepta sin demostración
pero que trata de sobre un campo limitado de la matemática.
Ejemplo.- “Existen infinitos puntos”.
TEOREMA.- Es una proposición que para ser evidente requiere de una
demostración. Tiene dos partes: Hipótesis, que es la parte que se acepta
como verdad. Tesis: Es la parte que se debe demostrar.
Ejemplo: “La suma de los ángulos interiores de un triángulo vale dos ángulos
rectos.
COROLARIO.- Es una proposición que se desprende de un teorema.
Ejemplo: La suma de los ángulos agudos de un triángulo rectángulo vale 90°
LEMA.- Es una proposición utilizada como parte de la hipótesis de un
teorema.

8. Inicio
POSTULADO 1.- Dos puntos diferentes en el plano determina una recta
POSTULADO 2 (Postulado de la Regla).- Podemos establecer una
correspondencia biunívoca entre los puntos de una recta y los números
reales, de manera que la distancia entre los puntos es el valor absoluto de
la diferencia de los números correspondientes.
Dados dos puntos P(x), Q(y) sobre una recta l, la distancia de P a Q se
denota d(P,Q) y se define:
d(P,Q) = |y - x|
Ejemplo:
1.- Hallar la distancia entre los puntos: M(5) y N(16).
d(M,N) = |16 - 5| = |11| = 11 ó también
d(M,N) = |5 - 16| = |-11| = 11
2.- Hallar la distancia entre los puntos: P(-3) y N(9).
d(P,Q) = |9 – (-3)| = |12| = 12 ó también
d(P,Q) = |-3 - 9| = |-12| = 12

9. Inicio
PROPIEDADES DE LA DISTANCIA ENTRE DOS PUNTOS
1.- d(P,Q) ≥ 0
2.- d(P,Q) = 0 ⇔ P = Q
3.- d(P,Q) = d(Q,P)
4.- d(A,B) ≤ d(A,X) + (X,B)
X
A X B
A B
d(A,B) < d(A,X) + (X,B) d(A,B) = d(A,X) + (X,B)
Se cumple cuando A, X, B Se cumple cuando A, X,
son puntos no colineales B son puntos colineales

10. Inicio
POSICIONES RELATIVAS DE RECTAS EN EL PLANO
RECTAS SECANTES RECTAS PARALELAS
Oblicuas
Perpendiculares
(al insectarse forman * Dos rectas son paralelas si y
ángulos rectos) solo sí son coincidentes o su
intersección es el conjunto vacío.
* La intersección de
las rectas secantes es
un punto.

11. Inicio
SEPARACIÓN DE LA RECTA
Un punto de la recta separa a la recta en tres
subconjuntos: dos semirrectas y el punto
SEPARACIÓN DEL PLANO
M
M1 M2
Una recta en el plano, separa al plano entres subconjuntos
de puntos: dos semiplanos y la recta

12. Inicio
RESOLVER LAS ACTIVIDADES 12 Y 13 DEL LIBRO

13. Inicio