Este documento presenta un resumen de los conceptos básicos de circuitos eléctricos de corriente continua. Introduce los conceptos de circuito eléctrico, elementos de circuito como resistencias y fuentes, y la forma en que pueden conectarse en serie o en paralelo. Explica cómo calcular la corriente en un circuito simple y uno con resistencia interna en la fuente. Luego describe cómo calcular las resistencias equivalentes para elementos en serie y paralelo. Finalmente, introduce las transformaciones entre conexiones en triángulo y estrella, así como








![Física General III CIRCUITOS DE CORRIENTE CONTÍNUA Toribio Córdova C.
VI. CIRCUITOS RC.
6.1 Proceso de carga de un capacitor
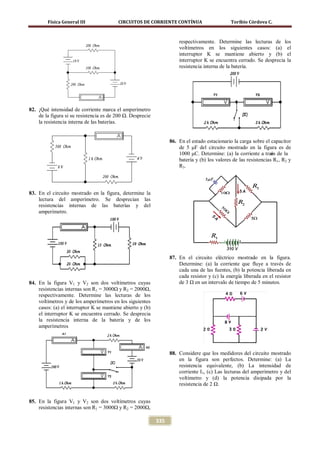
Consideremos el circuito eléctrico formado por una fuente de fem ε, una resistencia R, un condensador C y un
interruptor S, conectado como se muestra en la figura 7.13a.
(a) (b)
Figura 7.13. (a) diagrama del circuito RC para t < 0 y (b) diagrama de un circuito RC para t > 0
Cuando el interruptor S se encuentra abierto la corriente a través del circuito es nula y el capacitor se encuentra
completamente descargado, es decir [q(t = 0) =0]. Si en el instante t = 0 se cierra el interruptor S, comenzará a
fluir corriente a través del circuito como se muestra en la figura 7.13b. Esta corriente no es constante sino que
depende del tiempo. En particular la corriente instantánea en el circuito inmediatamente después de cerrado el
circuito es
ε
I0 = (7.25)
R
En este instante, la diferencia de potencial entre los terminales de la batería es la misma que en los extremos del
resistor. Conforme transcurre el tiempo el capacitor comienza a cargarse y la diferencia de potencial entre sus
bornes comienza a aumentar progresivamente. Siendo el voltaje a su través en cualquier tiempo
q (t )
VC (t ) = (7.26)
C
Aplicando la segunda ley de Kirchhoff al circuito se obtiene
q (t )
ε − I (t ) R −
=
0
C
dq q
ε
= R + (7.27)
dt C
Donde se considera que la corriente en el circuito es I = +dq/dt. Debido a que la corriente I debe ser la misma en
todas las partes del circuito, la corriente a través de la resistencia R es igual a la razón de cambio de la carga en
las placas del capacitor. El flujo de corriente en el circuito será continuo e irá decreciendo a medida que el
capacitor vaya incrementando su carga. El flujo de corriente finalizará cuando el capacitor se haya cargado
completamente, adquiriendo una carga total Q. Ello se vuelve evidente cuando escribimos la ecuación en la
forma.
dq q
R = ε− (7.28)
dt C
Para determinar la carga en cualquier instante sobre el capacitor la ecuación diferencial se escribe en la forma
dq 1 q
= (ε − ) (7.29)
dt R C
Esta ecuación puede ser resuelta usando el método de separación de variables. El primer paso es separar los
términos que involucran a la carga y al tiempo. Es decir
305](https://image.slidesharecdn.com/capitulovii-circuitosdecorrientecontinua-121021140729-phpapp01/85/CIRCUITOS-DE-CORRIENTE-CONTINUA-9-320.jpg)








![Física General III CIRCUITOS DE CORRIENTE CONTÍNUA Toribio Córdova C.
Agrupando las ecuaciones para resolverlas se tiene
( r + R2 + Rx ) I a − R2 I b − Rg I c =
ε
R2 I a − ( R1 + R2 + Rg ) I b + Rx I c =
0 (7.59)
Rx I a + Rg I b − ( R3 + Rx + Rg ) I c =
0
Resolviendo dichas ecuaciones se tiene
ε R2 R3 + ε R2 Rx + ε R2 Rg + ε Rx Rg
Ib =
∆ (7.60)
ε R2 Rg + ε R1 Rx + ε Rx R2 + ε Rx Rg
Ic =
∆
La intensidad de corriente que pasa por el galvanómetro será
ε
I g = Ib − Ic = [ R2 R3 − R1Rx ] (7.61)
∆
Cuando el puente se encuentra en equilibrio la corriente que fluye a través de dicho instrumento es nula.
Por lo tanto
R2 R3 − R1 Rx =
0 (7.62)
R2
Rx = R3 (7.63)
R1
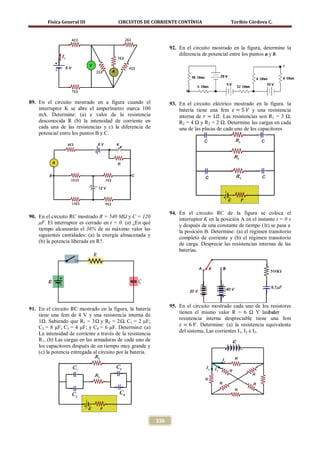
8.5. El potenciómetro
El potenciómetro es un circuito que permite determinar fuerzas electromotrices de baterías, pilas, etc,
comparándolas con fems patrones. La batería E1cuya fem es ε1 es mayor que la fem εx .
Figura 7.29. Circuito denominado potenciómetro utilizado para determinar fems desconocidas.
Para determinar la fem desconocida εx se procede de la siguiente manera:
Se conecta el conmutador S a la fem ε0 y se ajustan los terminales deslizantes T y T’ hasta que no fluya
corriente a través del galvanómetro. Si en esta posición la resistencia entre T y T’ es R1, entonces la
diferencia de potencial entre T y T’ será
∆VTT ' =
R1 I1
314](https://image.slidesharecdn.com/capitulovii-circuitosdecorrientecontinua-121021140729-phpapp01/85/CIRCUITOS-DE-CORRIENTE-CONTINUA-18-320.jpg)


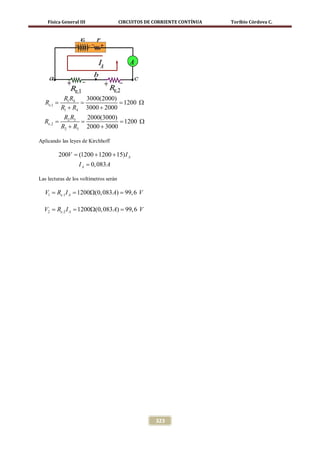
 ⇒ R 2,14 Ω
= =
3
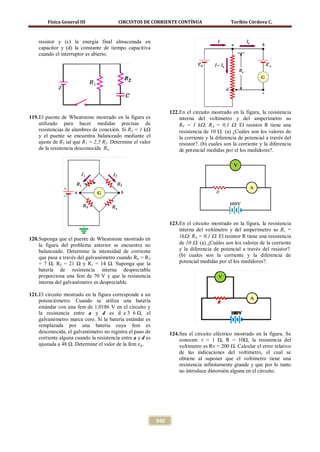
Problema 04
Solución Para el circuito mostrado en la figura. (a) Encuentre
la diferencia de potencial entre los puntos a y b. (b)
En la figura se muestra el sentido de las corrientes si laos puntos a y b están conectados por un cable
escogidas y las polaridades en las resistencias. con resistencia despreciable, encuentre la corriente
en la batería de 12 V
Aplicando la primera ley de Kirchhoff al nudo d se
tiene Solución
I A + I1 =
I2 Parte a. En la figura se muestra el sentido de la
corriente y las polaridades en las resistencias.
2A + I1 = I2 (1) Observe que como los puntos a y b no se
Aplicando la segunda ley de Kirchhoff a la malla encuentran en contacto por esa línea no habrá flujo
abcefga se tiene de corriente
∆Vε + ∆V10 Ω + ∆V2 Ω + ∆VR = 0
ε − 10Ω( I A ) − 2 I A − LecV =
0
ε − 10 Ω(2 A) − 2(2 A) − 5 V =
0
ε = 29 V (2)
Aplicando la segunda ley de Kirchhoff a la malla
defgh se tiene
Aplicando la segunda ley de Kirchhoff a la malla
cdefc se tiene
318](https://image.slidesharecdn.com/capitulovii-circuitosdecorrientecontinua-121021140729-phpapp01/85/CIRCUITOS-DE-CORRIENTE-CONTINUA-22-320.jpg)


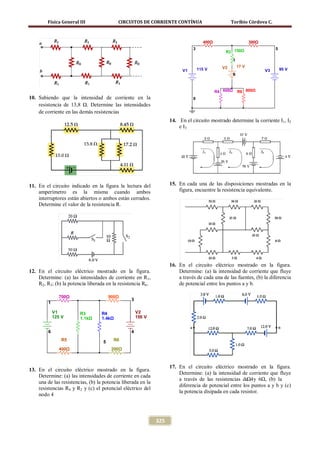
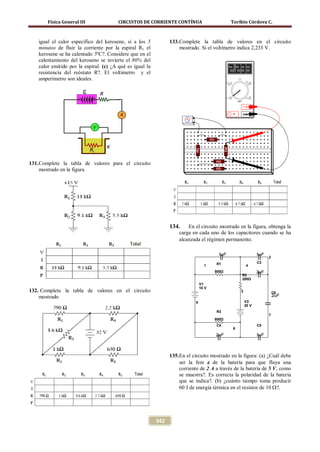
![Física General III CIRCUITOS DE CORRIENTE CONTÍNUA Toribio Córdova C.
Se procede a determinar el voltaje y la carga en el si el amperímetro marca 6 A?. Desprecie la
capacitor resistencia del generador y del amperímetro y
considere que R2 = 30 Ω.
∆VC ==
∆VR 600 k Ω
∆VC I ∞ ( R) 2, 78.10−5 A(600.103 Ω)
= =
∆VC = 68 V
16,
Qmax = c ) = (2,5.10−6 F )
∆VC (C 16, 68V
Qmax = 41, 70 µ F
Parte (c). Al abrir el interruptor S el condensador
cargado completamente se descarga a través del
resistor R = 600 kΩ. Por tanto se tiene
Solución
En la figura se muestran las corrientes y las
polaridades en las resistencias.
Aplicando la segunda ley de Kirchhoff se tiene
q
∆VC + ∆VR = 0 ⇒ − RI = 0
C
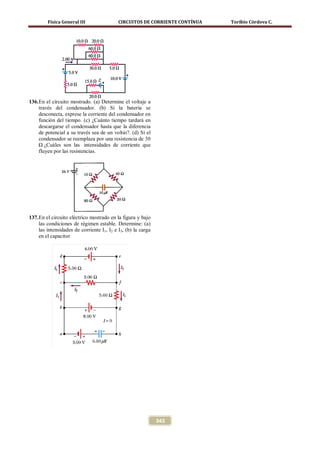
q dq dq dt
− R(− ) =⇒ 0 =−
C dt q RC Aplicando la primera ley de Kirchhoff al nudo se
q dq 1 t tiene
∫Qmax q RC ∫0 dt
= −
I A I1 + I 2
=
q t 6 A I1 + I 2
=
ln = −
Qmax RC
Las resistencias R1 y R2 se encuentran en paralelo
q = Qmax e − t / RC por lo que sus diferencias de potenciales entre sus
extremos serán iguales. Es decir
q = [41, 70e − t /1,5 ]µ F
∆VR2 = R1 ⇒ R2 I 2 =I1
∆V R1
La intensidad de corriente será 30 I 2 = 60 I1
dq d I 2 = 2 I1
I = = [41, 70e − t /1,5 ]µ F
− − Resolviendo simultáneamente estas ecuaciones se
dt dt tiene
I = 2, 78.10−5 e − t /1,5 A 6 A I1 + 2 I1
=
I1 = 2 A
Problema 07
La potencia eléctrica disipada en la espiral R1 es
El calorímetro K tiene una espiral de resistencia
R1 = 60 Ω. La espiral R1 se conecta a la red como
se muestra en la figura. ¿A cuántos grados se
= I= (2 A) 2 (60Ω)
P1
2
1 R1
calentarán 480 g de agua con que se llena el P = 240 W
1
calorímetro, durante 5 minutos de fluir la corriente,
321](https://image.slidesharecdn.com/capitulovii-circuitosdecorrientecontinua-121021140729-phpapp01/85/CIRCUITOS-DE-CORRIENTE-CONTINUA-25-320.jpg)

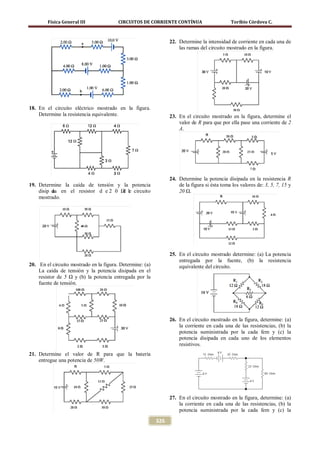
(I [0,
(a) el interruptor S se encuentra abierto y (b) el
interruptor S se encuentra cerrado. V1 = 120 V
La lectura del voltímetro V2 será
V2 = a − I b ) R1 = 079 A − 0, 039 A](2000Ω)
(I [0,
V1 = 80 V
Parte (b) Determinación de las lecturas de los
medidores cuando S se encuentra cerrado. Es decir,
el circuito se grafica en la forma mostrada en la
figura
Solución
Parte (a) Determinación de las lecturas de los
medidores cuando S se encuentra abierto. Note que
los voltímetros tienen resistencias considerables
comparadas con las dos resistencias R3 y R4.
Uniendo los puntos de igual potencial se observa
que R1 se encuentra en paralelo con R4 de igual
forma los resistores R2 y R3 están en paralelo.
Entonces sus resistencias equivalentes serán
Aplicando las ecuaciones de mallas circulantes de
Maxwell, se tiene
322](https://image.slidesharecdn.com/capitulovii-circuitosdecorrientecontinua-121021140729-phpapp01/85/CIRCUITOS-DE-CORRIENTE-CONTINUA-26-320.jpg)